1.1 Постановка задачи целочисленного программирования

По смыслу значительной части экономических задач, относятся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.

Задача линейного целочисленного программирования формируется следующим образом: найти такое решение (план) X = (x₁,x₂,...,x_n), при котором линейная функция

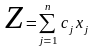(1)

принимает максимальное или минимальное значение при ограничениях

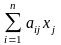=b_i, i=1, 2…, m. (2)

х_j ³ 0, j=1, 2,..., п. (3)

x_j - целые числа (4)

2. Методы решения задач целочисленного программирования

На первый взгляд наиболее естественным методом решения задач целочисленного программирования является метод округления, реализация которого состоит из двух этапов. На первом этапе находят оптимальное решение задачи линейного программирования с ослабленными ограничениями, соответствующей рассматриваемой задаче целочисленного программирования. На втором этапе значения переменных в оптимальном решении X*, не являющиеся целыми, округляют так, чтобы получить допустимое решение X** с целочисленными значениями.

Соблазнительность использования метода округления понятна, особенно если погрешность округления невелика по сравнению со значениями округляемых переменных. Однако практическая реализация метода округления может привести к допустимому решению, значимо отличающемуся от оптимального решения исходной задачи целочисленного программирования.

Несостоятельность метода округления как общего метода решения задач целочисленного программирования обусловлена не только возможностью получения неоптимального решения. Дело заключается в том, что многие задачи математического программирования, не имеющие на первый взгляд никакого отношения к полностью или частично целочисленным задачам, могут быть сформулированы как задачи целочисленного программирования, в которых переменные модели принимают значения из множества {0, 1}. В этой ситуации процедура округления является логически неприемлемой.

Для иллюстрации основной идеи методов решения задач целочисленного программирования, известных как методы отсечений, рассмотрим полностью целочисленную задачу, множество допустимых решений которой изображено на рисунке 1. Допустимым решениям этой задачи соответствуют не все точки множества G допустимых решений, а лишь те, координаты которых удовлетворяют требованию целочисленности. Теоретически из множества G всегда можно выделить такое подмножество G*, что (см. рис. 1):

а) оно содержит все точки множества G, координаты которых удовлетворяют требованию целочисленности;

б) оно является выпуклым множеством;

в) координаты всех его крайних точек удовлетворяют требованию целочисленности.

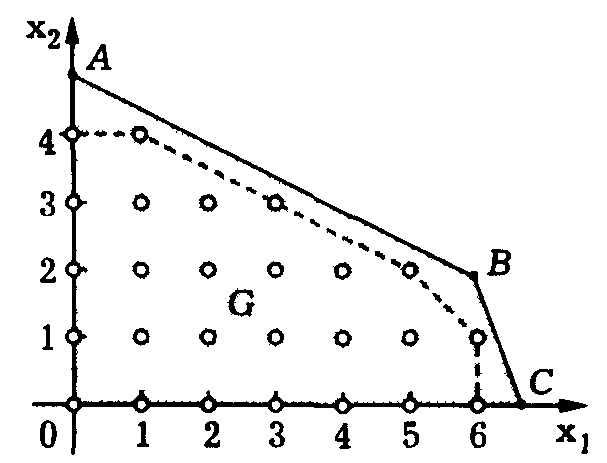
Рис. 1

Если в рассматриваемой полностью целочисленной задаче множество G допустимых решений заменить множеством G*, то это не может привести к изменению ее оптимального решения, так как G* получено из G путем отсечения от него подмножества, заведомо не содержащего допустимых решений, удовлетворяющих требованию целочисленности. Но в этом случае оптимальное решение задачи линейного программирования с ослабленными ограничениями и множеством G* допустимых решений соответствует крайней точке множества G*. Как следствие, оно удовлетворяет требованию целочисленности и обеспечивает экстремальное значение целевой функции не только на G*, но и на G, т.е. является оптимальным решением исходной полностью целочисленной задачи. Основные различия в методах отсечений связаны с процедурами выделения подмножества G* множества допустимых решений задачи целочисленного программирования.

В основе комбинаторных методов решения задач целочисленного программирования лежит идея перебора всех элементов G множества допустимых решений, удовлетворяющих требованию целочисленности, с целью нахождения оптимального решения. При этом за счет использования различных специальных процедур, как правило, непосредственно рассматривают лишь часть элементов G, удовлетворяющих требованию целочисленности, а оставшиеся элементы учитывают некоторым косвенным образом.

Наиболее известным комбинаторным методом является метод ветвей и границ, использующий процедуру решения задачи линейного программирования с ослабленными ограничениями, соответствующей исходной задаче целочисленного программирования. Если оптимальное решение X* задачи линейного программирования с ослабленными ограничениями не удовлетворяет требованию целочисленности (на рисунке 2 этому решению соответствует точка В), то из множества G допустимых решений выделяют два непересекающихся выпуклых подмножества К₁ и К₂, содержащих все допустимые решения из G, удовлетворяющих требованию целочисленности и не содержащих X* (см. рис. 2). Это позволяет заменить рассматриваемую задачу целочисленного программирования совокупностью двух эквивалентных ей задач с множествами допустимых решений К₁ и К₂ соответственно, так как 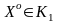или .

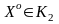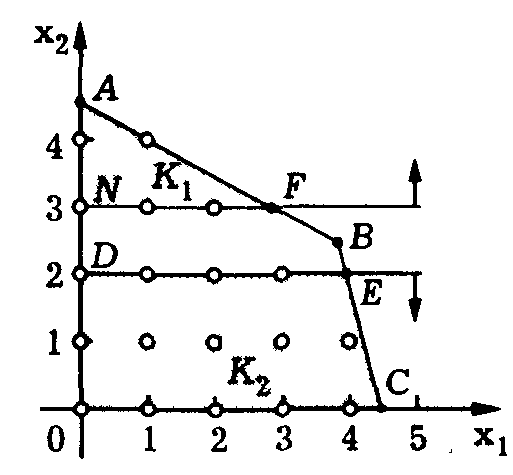
Рис. 2

Комбинаторные методы широко используют для решения задач булева программирования, т.е. для решения полностью целочисленных задач, переменные которых принимают значения из множества {0, 1}. Эти переменные называют булевыми переменными. Свойства булевых переменных позволяют существенно упростить процедуры поиска оптимального решения.

К настоящему времени разработано значительное количество частных методов решения конкретных типов задач целочисленного программирования. Тем не менее, почти все эти методы и их модификации можно описать на основе единой принципиальной схемы, состоящей из трех элементов.

Элемент 1. Предусматривается процедура формирования и решения последовательности взаимосвязанных задач, которые называют задачами, порожденными исходной задачей, или задачами-истоками. При этом оптимальное решение по крайней мере одной из задач-истоков должно совпадать с оптимальным решением породившей их задачи.

Элемент 2. Каждой задаче, порожденной исходной задачей, ставится в соответствие так называемая ослабленная задача (задача с ослабленными ограничениями), оптимальное решение которой может быть найдено с гораздо меньшими затратами, чем оптимальное решение соответствующей ей задачи-истока. Специфика ослабленной задачи чаще всего заключается в том, что ее система ограничений является менее жесткой по сравнению с системой ограничений задачи-истока и определяет множество допустимых решений, содержащее все допустимые решения задачи-истока. Как правило, в целочисленном программировании ослабленная задача представляет собой задачу линейного программирования с ограничениями, более слабыми, чем в соответствующей целочисленной задаче-истоке. Очевидно, что если ослабленная задача не имеет допустимых решений, то их не имеет и задача-исток. В некоторых модификациях методов целочисленного программирования целевая функция ослабленной задачи также может отличаться от целевой функции задачи-истока. В этом случае оптимальное значение целевой функции ослабленной задачи (т.е. значение, соответствующее оптимальному решению) должно быть не меньше оптимального значения целевой функции задачи-истока, если речь идет о задаче максимизации. Кроме того, оптимальное значение целевой функции ослабленной задачи определяет (для задачи максимизации) верхнюю границу для оптимального значения целевой функции задачи-истока.

Элемент 3. В результате анализа решения ослабленной задачи в зависимости от специфики метода, как правило, принимается решение, относящееся к задаче-истоку:

а) исключить ее из рассмотрения;

б) заменить одной порожденной задачей, выбранной по специальному правилу из определенной совокупности;

в) заменить системой порожденных задач.

Следует отметить, что существуют и другие подходы к решению задач целочисленного программирования, которые в общем случае не гарантируют нахождения оптимального решения, но приводят к допустимому решению, близкому (в смысле значения целевой функции) к оптимальному, а иногда и совпадающему с ним. В основе одного из таких подходов лежит идея использования случайной выборки допустимых решений с последующим улучшением (в смысле значения целевой функции) каждого из них, когда возможность улучшения допустимого решения достаточно просто обнаружить.

В моей курсовой мы с вами рассмотрим такие методы как : метод ветвей и границ, метод Гомори, циклический алгоритм целочисленного программирования, полностью целочисленный алгоритм.