2. Метод Рунге-Кутта.
Рассмотрим
задачу Коши (1). Обозначим через
приближенное значение искомого решения
в точке
.
По методу Рунге-Кутта вычисление
приближенного значения
в следующей точке
производится по формулам:
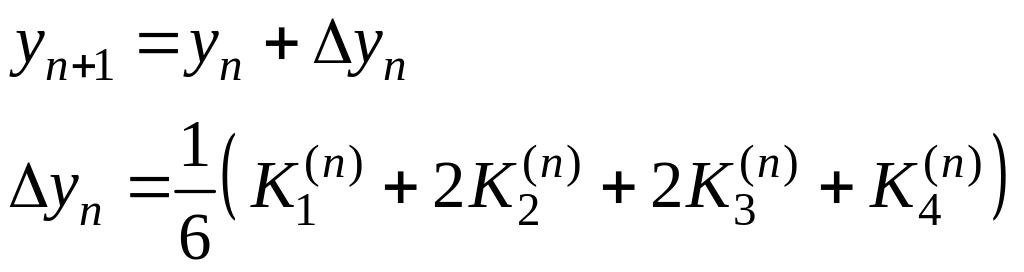, (7)
Где
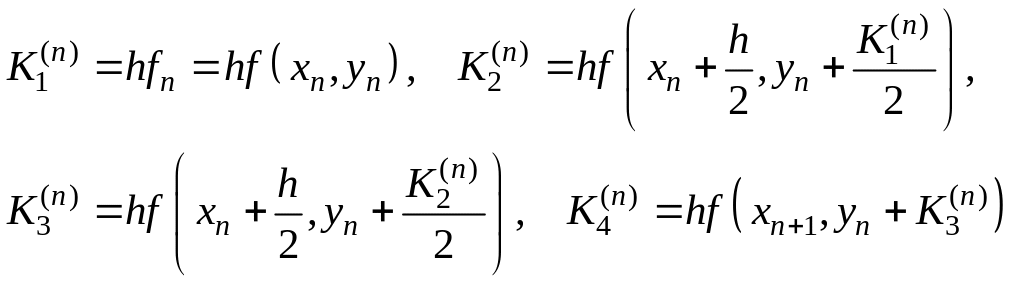
Многошаговые методы
1. Формулировка методов
Для решения задачи Коши
(1)
Введем
сетку
с постоянным шагом
(построим систему равноотстоящих точек).
Обозначим через
функции, определенные на сетке
.
Линейным
–шаговым
разностным методом называется
система разностных уравнений
(2)
где
– числовые коэффициенты, не зависящие
от
,
причем
.
Уравнение
(2) следует рассматривать как рекуррентное
соотношение, выражающее новое значение
через найденные ранее значения
.
Расчет
начинается с
,
т.е. с уравнения
Для
начала расчета необходимо задать
начальных значений
.
Значение
определяется исходной задачей (1):
,
величины
можно вычислить, например, методом
Рунге-Кутта.
Наибольшее
распространение получили методы
Адамса,
которые представляют собой частный
случай многошаговых методов (2), когда
производная
аппроксимируется только по двум точкам,
и
,
т.е.
.
Т.о. методы Адамса имеют вид
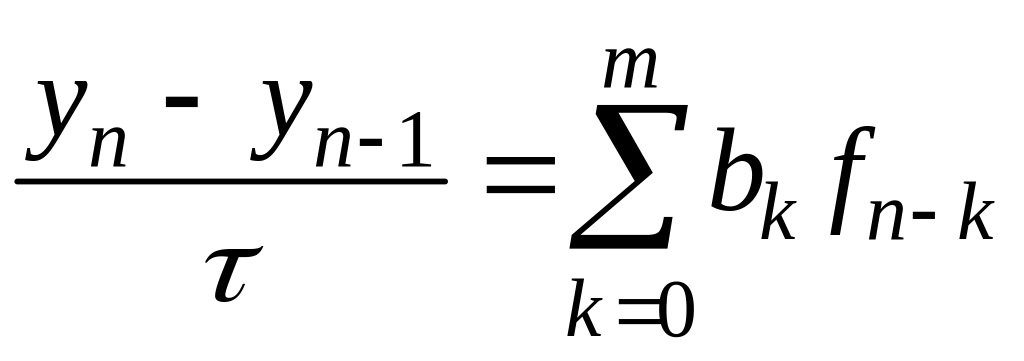(10)
.
В случае
методы Адамса называются явным,
в случае
– неявными.
Методы решения краевых задач. Конечно-разностный метод решения краевой задачи.
Принципиальным отличием краевой задачи от задачи Коши для ОДУ является задание дополнительных (краевых или граничных) условий более чем в одной точке независимой переменной (в задаче Коши дополнительные условия задаются в одной точке, называемой начальной)
Постановка линейных краевых задач для оду 2-го порядка.
Пусть
на отрезке
определена дважды непрерывно
дифференцируемая функция
,
поведение которой описывается линейным
неоднородным уравнением 2-го порядка.
Если
на границах
и
заданы значения искомой функции
,
,
то такие условия называются граничными
условиями первого рода, а
задача
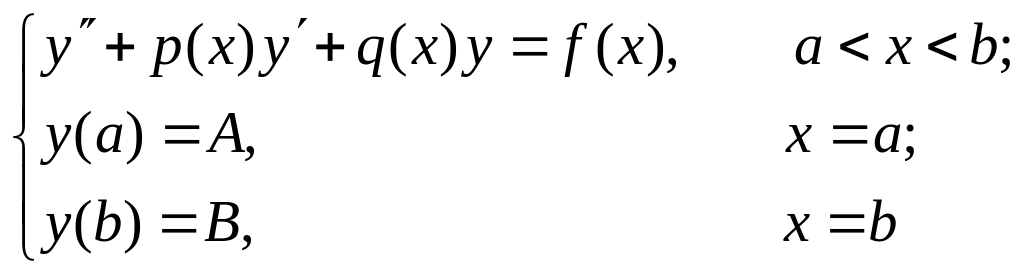
называется первой краевой задачей для ОДУ
Если на границах заданы значения производных искомой функции, то такие условия называются граничными условиями второго рода:
,
а соответствующая задача – второй краевой задачей.
Если на границах заданы линейные комбинации искомой функции и ее первой производной:
то такие условия называются граничными условиями третьего рода, а соответствующая задача– третьей краевой задачей.
Чаще всего на разных границах задаются граничные условия различных родов. Такие задачи называют краевыми задачами со смешанными краевыми условиями.
Конечно-разностный метод решения краевой задачи.
Рассмотрим линейное ДУ
, (1)
с двухточечными краевыми условиями
, (2)
где
– известные непрерывные на отрезке
функции,
–
заданные постоянные, причем
О
дним
из наиболее простых методов решения
этой краевой задачи является сведение
ее к системе конечно-разностных уравнений.
Суть конечно-разностных методов:
Введем
разностную сетку на
,
.
Решение
исходной задачи будем искать в виде
сеточной функции
,
Значения
в точках деления
производных искомой функции
обозначим соответственно через
Введем также обозначения
Предполагаем, что решение существует и единственно. Введем разностную аппроксимацию производных следующим образом (воспользуемся симметричными конечно-разностными отношениями):
(3)
Для
концевых точек
полагаем
(4)
Таким
образом, получена СЛАУ из
уравнений с
неизвестными
.
с трехдиагональной матрицей коэффициентов.
Для производных в концевых точек обычно приходится пользоваться формулами (4). Но в этом случае СЛАУ аппроксимирует дифференциальную задачу в целом только с первым порядком (из-за аппроксимации в граничных точках), однако сохраняется трехдиагональная структура матрицы коэффициентов сохраняется.
Полученную систему
(5)
можно представить в виде следующей СЛАУ с трехдиагональной матрицей
.
где
и дополнительно уравнения (6) (при использовании граничных условий и формул (4)).
(6)
т.е.
Для
полученной линейной трехдиагональной
системы алгебраических уравнений при
достаточно малых шагах сетки
и
выполнены условия преобладания
диагональных элементов, что гарантирует
устойчивость
счета и корректность
применения метода прогонки
для решения этой системы.
1 Лат. a priori и a posteriori означают соответственно «до опыта» и «из опыта», т.е. априорной оценкой можно воспользоваться до начала счета, апостериорной – лишь после проведения -й итерации.