
- •1. Метод Данилевского
- •1.1 Метод Гаусса.
- •1.2 Метод Гаусса с выбором главного элемента. ( )
- •1.3 Метод оптимального исключения ( )
- •1.4 Метод прогонки.
- •II. Методы, основанные на разложении матрицы коэффициентов.
- •2.1. Метод квадратного корня (случай эрмитовой матрицы)
- •2.2 Частный случай метода квадратного корня (случай симметричной матрицы)
- •2.3 Схема Халецкого (случай матрицы с отличными от 0 глав. Минорами).
- •Приближенные (итерационные) методы.
- •2.1 Метод простой итерации.
- •2.2 Метод Якоби.
- •2.3 Метод Зейделя.
- •2. Решение полной проблемы собственных чисел.
- •1. Метод Данилевского
- •2. Итерационный метод вращений.
- •Решение нелинейных уравнений.
- •1.2.1 Метод половинного деления (метод дихотомии).
- •1.2.2 Метод Ньютона или метод касательных
- •1) Существование производных 1-го и 2-го порядков;
- •1.2.3 Метод хорд. Метод секущих.
- •1.2.4 Метод простой итерации.
- •III. Решение дифференциальных уравнений.
- •Задачи с начальными условиями для оду (задача Коши).
- •Численные методы решения дифференциальных уравнений Одношаговые методы. Метод Эйлера и его модификации
- •Одношаговые методы. Метод Эйлера и его модификации.
- •1 Метод Эйлера
- •2. Метод Рунге-Кутта.
- •Многошаговые методы
- •1. Формулировка методов
- •Постановка линейных краевых задач для оду 2-го порядка.
- •Конечно-разностный метод решения краевой задачи.
III. Решение дифференциальных уравнений.
При решении ОДУ без каких-либо условий получается множество решений. Для получения единственного решения задают дополнительные условия. Если задано значение функции в начальный момент времени, то условия называются начальными, а полученная задача называется задачей Коши; если условия задаются на границе, то их называют граничными или краевыми, а саму задачу – краевой. Если заданы и начальные и граничные условия задачу называют смешанной краевой задачей.
Задачи с начальными условиями для оду (задача Коши).
Задача
Коши для
дифференциального уравнения
-го
порядка заключается в отыскании
![]() ,
удовлетворяющей уравнению (1) и начальным
условиям (2)
,
удовлетворяющей уравнению (1) и начальным
условиям (2)
![]() (1)
(1)
![]() , (2)
, (2)
где
![]() –
заданные числа.
–
заданные числа.
Численные методы решения дифференциальных уравнений Одношаговые методы. Метод Эйлера и его модификации
Рассматриваются две группы численных методов решения задачи Коши.
Одношаговые методы, в которых для нахождения решения в некоторой точке отрезка используется информация лишь в одной предыдущей точке (методы Эйлера, Рунге–Кутта).
Многошаговые методы, в которых для отыскания решения в некоторой точке используется информация о решении в нескольких предыдущих точках (метод Адамса)
Опр
1. Метод
сходится на отрезке
![]() ,
если он сходится в каждой точке
,
если он сходится в каждой точке
![]()
Опр
2. Метод
имеет р-й порядок точности, если существует
число р>0 такое, что![]() при
при
![]()
Опр
3. Сеткой
на отрезке
![]() называется любое конечное множество
точек этого отрезка. Функция, определенная
в точках сетки, называется сеточной
функцией.
называется любое конечное множество
точек этого отрезка. Функция, определенная
в точках сетки, называется сеточной
функцией.
В численных методах используются замены производных конечными разностями:
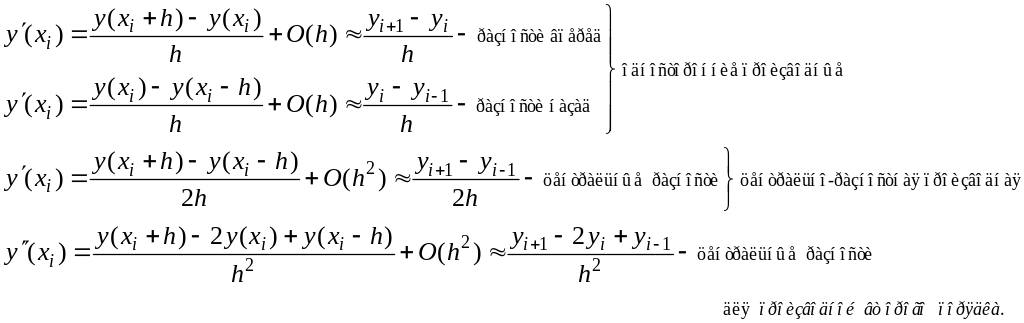
Одношаговые методы. Метод Эйлера и его модификации.
Метод Эйлера является простейшим методом решения задачи Коши и имеет невысокую точность, поэтому на практике его используют достаточно редко. Однако на его основе в дальнейшем легче объяснить алгоритмы более эффективных методов.
Рассмотрим задачу Коши для ОДУ 1-го порядка.
![]() (1)
(1)
![]() (2)
(2)
Требуется
найти функцию
![]() ,
которая удовлетворяет уравнению (1) на
интервале
,
которая удовлетворяет уравнению (1) на
интервале
![]() и начальному условию (2) в точке
.
и начальному условию (2) в точке
.
Приведем без доказательства теорему существования и единственности задачи Коши:
Теорема
1. Пусть
в области
![]() функция
функция
![]() непрерывна. Тогда на некотором отрезке
непрерывна. Тогда на некотором отрезке
![]() существует решение уравнения (1),
удовлетворяющее условию (2).
существует решение уравнения (1),
удовлетворяющее условию (2).
Если
в области
![]() функция
удовлетворяет условию Липшица
функция
удовлетворяет условию Липшица
![]() ,
,
то указанное решение единственно.
Проведем
разбиение отрезка
![]() на
частей:
на
частей:
![]() . (3)
. (3)
Найдем
приближенные значения решения
![]() в точках
в точках
![]() .
.
1 Метод Эйлера
Рассмотрим
уравнение (1) в точках
![]() и заменим производную
и заменим производную
![]() . (4)
. (4)
Подставим в (1), получим
![]()
Введем
обозначения
![]() ,
получим
,
получим
![]()
– это явная несимметричная схема, 1-го порядка аппроксимации
Рекуррентная
формула метода Эйлера для приближенных
значений
![]() :
:
![]() . (5)
. (5)
Можно рассмотреть неявную схему, формула будет иметь вид
![]() (5’)
(5’)
Недостатки метода Эйлера: малая точность, систематическое накопление ошибок
Модификации
метода Эйлера (погрешность
![]() ).
).
Для повышения точности метода Эйлера применяют следующие приемы.
Первый улучшенный метод (метод серединных точек) для решения задачи (1), (2) состоит в том, что сначала вычисляют промежуточную (серединную) точку с координатами
![]() , (7)
, (7)
где
![]() .
Затем находят число
.
Затем находят число
![]() , (8)
, (8)
определяющее уточненное направление, и берут
![]() . (9)
. (9)
Второй улучшенный метод (метод Эйлера-Коши).
Сначала находят приближенное значение решения по методу Эйлера:
![]() , (10)
, (10)
исходя из которого определяют направление поля интегральных кривых
![]()
а затем уточняют его по формуле
![]() . (11)
. (11)
Этот метод называется методом Эйлера-Коши.
