II. Методы, основанные на разложении матрицы коэффициентов.
Такие методы основаны на представлении матрицы А коэффициентов системы в форме произведения треугольных матриц. Это позволяет свести решение заданной системы к последовательному решению двух систем с треугольными матрицами, что является задачей более простой, так как в них неизвестные находятся последовательно. Иногда вводят еще диагональную матрицу.
2.1. Метод квадратного корня (случай эрмитовой матрицы)
Найдем
такую правую треугольную матрицу
и диагональную матрицу
,
элементы которой равны 1 или –1, чтобы
имела представление
(2)
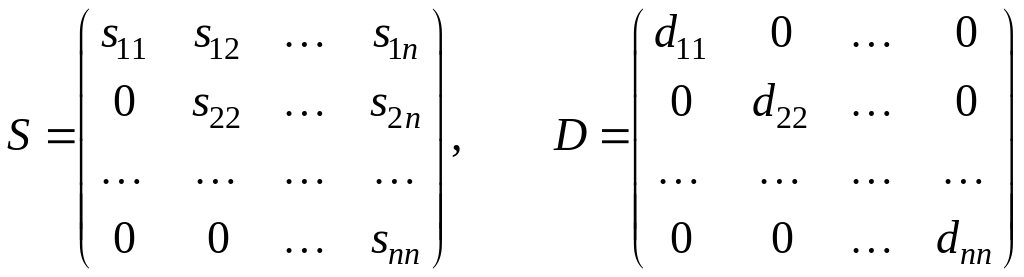
Если матрицы и найдены, то заданная система (1) может быть решена следующим путем:
,
где
есть нижняя треугольная матрица и
– вспомогательный вектор. Решение
системы (1) равносильно решению двух
треугольных систем
Замечание:
Алгоритм
–
разложения может оказаться численно
неустойчивым, гарантировать устойчивость
алгоритма можно в двух случаях – для
положительно определенных матриц А
и матриц с диагональным преобладанием.
2.2 Частный случай метода квадратного корня (случай симметричной матрицы)
Идея метода:
Метод основан на разложении матрицы на множители,
, (3)
где
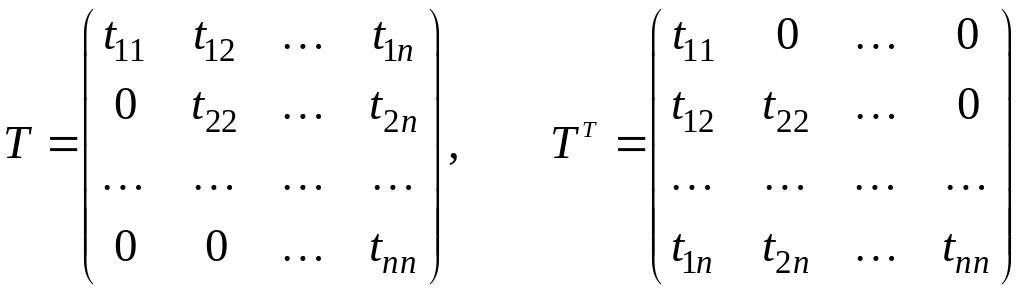
И решение системы (1) сводится к решению двух систем с треугольными матрицами:
(4)
Прямой ход:
Перемножая
матрицы
и
и приравнивая матрице
,
из (3) получим формулы для определения
Обратный ход:
После того, как матрица найдена, решаем задачу (4).
2.3 Схема Халецкого (случай матрицы с отличными от 0 глав. Минорами).
Рассматриваем
систему уравнений (1), где матрица
размера
такая, что ее главные миноры отличны
от нуля.
,
Теорема 1. Если главные миноры матрицы отличны от нуля:
то матрицу можно представить в форме
,
где
.
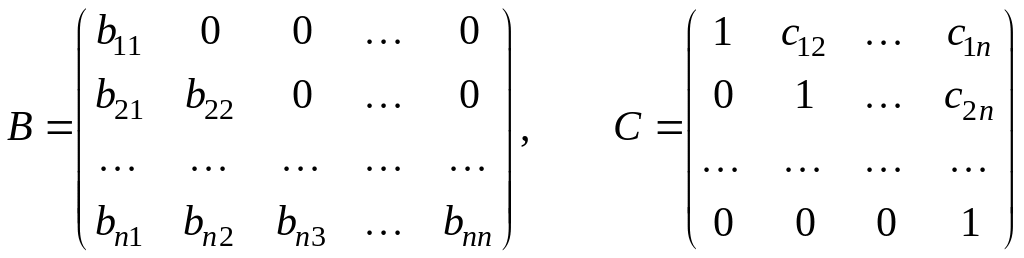Отсюда искомый вектор х может быть вычислен из цепи уравнений
Эта схема вычислений называется схемой Халецкого.
Решение систем линейных алгебраических уравнений (ЛАУ)
Приближенные (итерационные) методы.
2.1 Метод простой итерации.
Пусть дана система ЛАУ с неособенной матрицей.
(1)
Тем или иным способом система (1) может быть преобразована к эквивалентной ей системе вида
, (2)
где
– тот же вектор неизвестных, а
и
– некоторые новые матрица и вектор
соответственно.
В
методе
простой итерации
(МПИ) решение
системы (2) и, следовательно, решение
исходной системы (1) ищется как предел
последовательности векторов при
:
, (3)
где
– начальное приближение к точному
решению
системы.
Теорема
2. Пусть
.
Тогда при любом начальном приближении
МПИ (3)
сходится к единственному решению
задачи (2)
и при всех
справедливы оценки погрешности:
1) 
(апостериорная); (6)
2)
(априорная)1. (7)
Замечание
1. Априорная
оценка (7)
позволяет
подсчитывать заранее число итераций
,
достаточное для получения решения
с заданной точностью
при выбранном начальном приближении
.
Для этого нужно найти наименьшее целое
решение неравенства
относительно переменной
.
Апостериорной оценкой (6)
удобно пользоваться в процессе вычислений
и останавливать этот процесс, как только
выполнится неравенство
. (6`)
Иногда
используется более простое условие
остановки итерационного процесса
.
Это неравенство будет гарантией
выполнения неравенства
только в том случае, когда
.
Замечание 2. (О выборе начального приближения). Согласно теореме 1, сходимость МПИ (3) гарантируется при любом начальном приближении . Очевидно, итераций потребуется тем меньше, чем ближе к . Если нет никакой дополнительной информации о решении задачи (2) (например, может быть известным решение близкой задачи или грубое решение данной задачи) за обычно принимают вектор свободных членов системы (2). Априорная оценка (7) принимает вид
.
Таким образом, если задана точность , то
,
откуда
получаем априорную нижнюю оценку числа
итераций
при
:
. (8)
Неравенство (8) обычно дает завышенное число итераций .
Непосредственным следствием теоремы 2 и равенств
;
,
определяющих
кубическую и октаэдрическую норму
матрицы, являются следующие оценки
погрешности приближенного решения
:
,
, (9)
если
выполнено условие
,
и
,
, (10)
если
выполнено условие
.
Эти оценки можно еще усилить соответственно так:
(9`)
и 
. (10`)
МПИ в координатной форме имеет вид:
