Доп. вопросы к экзамену Численные методы ВМК 2012
ОГЛАВЛЕНИЕ
I. Численные методы алгебры
К численным методам алгебры относят:
1. численные методы решения систем алгебраических уравнений;
2. вычисление определителей, обращение матриц, нахождение собственных чисел и собственных векторов матрицы (проблема собственных чисел);
1. Решение систем линейных алгебраических уравнений (ЛАУ)
Точные (прямые) методы
I. Методы исключения неизвестных:
1.1 Метод Гаусса.
1.2 Метод Гаусса с выбором главного элемента.
1.3 Метод оптимального исключения
1.4 Метод прогонки.
II. Методы, основанные на разложении матрицы коэффициентов.
2.1. Метод квадратного корня (случай эрмитовой матрицы)
2.2 Частный случай метода квадратного корня (случай симметричной матрицы)
2.3 Схема Халецкого (случай матрицы с отличными от 0 глав. минорами).
Приближенные (итерационные) методы.
1. Метод простой итерации.
2. Метод Якоби
3. Метод Зейделя.
2. Решение полной проблемы собственных чисел.
1. Метод Данилевского
2. Метод вращений
II. Решение нелинейных уравнений.
Итерационные
методы вычисления изолированного корня
уравнения
:
1. Метод деления отрезка пополам (метод бисекций)
2. Метод секущих
3. Метод хорд (метод ложного положения)
4.Метод Ньютона или метод касательных
5. Метод простой итерации
III. Решение дифференциальных уравнений.
1. Задачи с начальными условиями для ОДУ (задача Коши).
Аналитические приближенные методы: метод последовательного дифференцирования, метод неопределенных коэффициентов, метод последовательных приближений
Численные методы: одношаговые (Эйлера, Рунге-Кутта), многошаговые (Адамса).
2. Краевые задачи
Конечно-разностный метод, метод прогонки.
Решение систем линейных алгебраических уравнений (ЛАУ)
Точные (прямые) методы
1.1 Метод Гаусса.
Рассмотрим
решение системы (1)
линейных уравнений с
неизвестными в общем виде.
Метод Гаусса – метод последовательного исключения переменных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
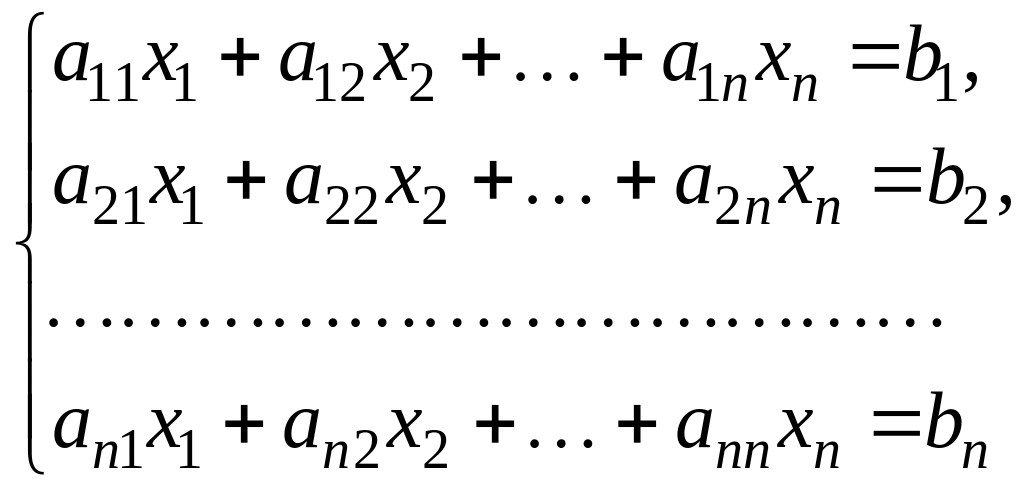(1)
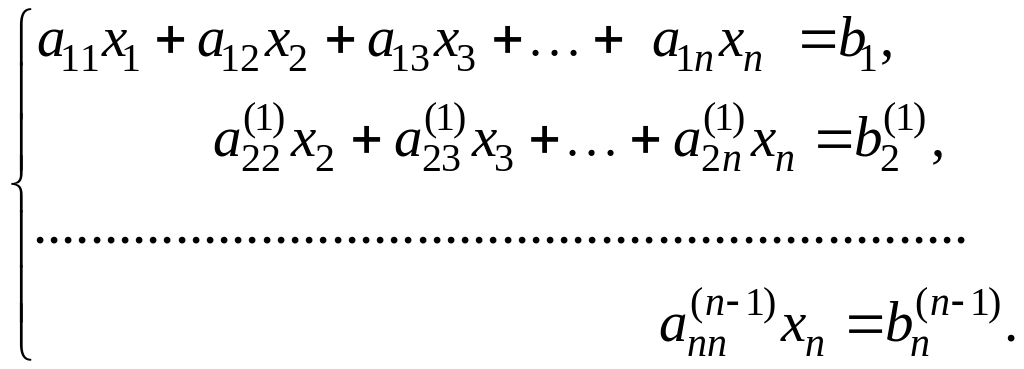(2)
Переход
системы (1) к равносильной ей системе
(2) составляет прямой
ход метода Гаусса. Обратный ход заключается
в нахождении неизвестных
из системы (2) .
Достоинства метода Гаусса:
менее трудоемкий (по сравнению с методом обратной матрицы и расчетами по формулам Крамера);
позволяет однозначно установить, совместна система или нет, а в случае совместности найти ее решения (единственное или бесконечное множество);
дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.
1.2 Метод Гаусса с выбором главного элемента. ( )
На
каждом шаге при прямом методе Гаусса
мы делили на элемент
– этот элемент назывался ведущим. Может
получиться так, что элемент близок к 0,
сл-но, коэф-ты в уравнении большие, сл-но,
увеличивается арифметич. погрешность
при обратном ходе. В этом случае удобнее
применять метод
Гаусса с выбором главного элемента.
Основная
идея метода состоит в том, что на
очередном шаге исключать не следующее
по номеру неизвестное, а то неизвестное,
коэффициент при котором является
наибольшим по модулю. Таким образом, в
качестве ведущего элемента здесь
выбирается
главный, т.е. наибольший по модулю
элемент.
1.3 Метод оптимального исключения ( )
Прямой и обратный ход совмещены.
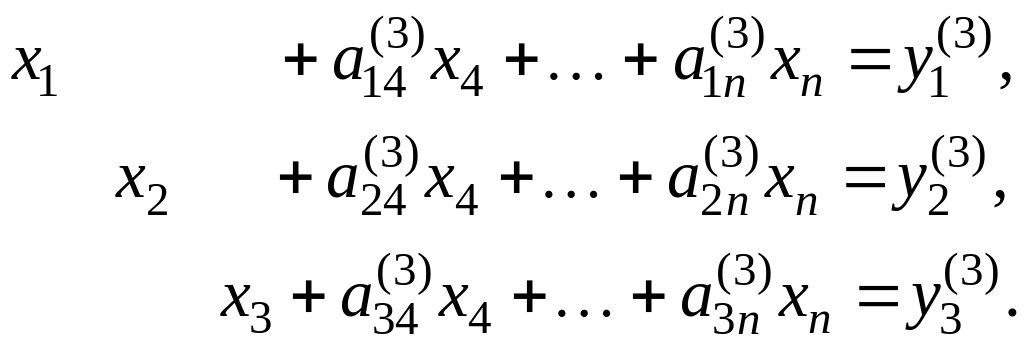
Остальные уравнения в системе (1) преобразуются аналогичным образом. В этом методе экономится память, т.о. можно решать системы с числом неизвестных в два раза больше метода Гаусса. В методе оптимального исключения обратный ход метода Гаусса здесь видоизменен и соединен с прямым ходом.
1.4 Метод прогонки.
Это частный случай метода Гаусса с ленточной матрицей вида (М1). Применяя к такой системе метод Гаусса мы приходим к системе матрицы (М2)
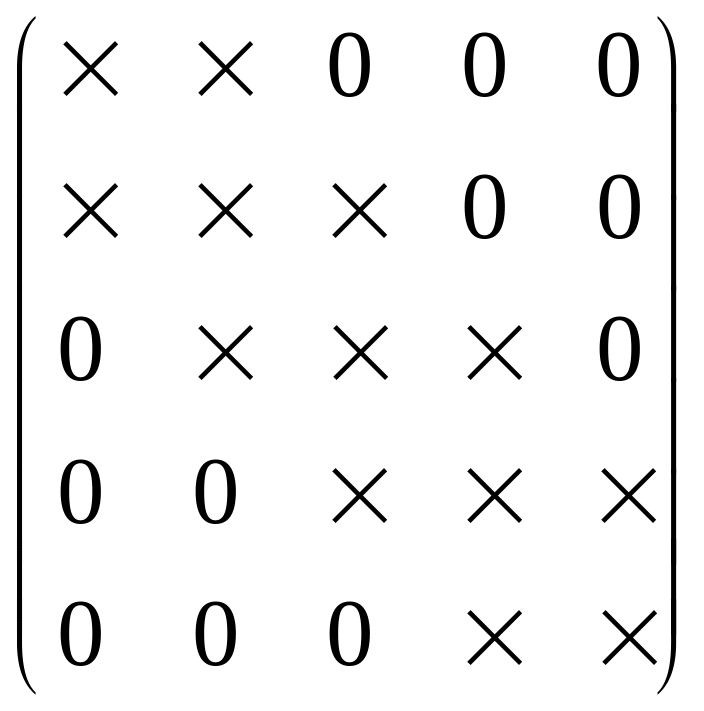(М1)
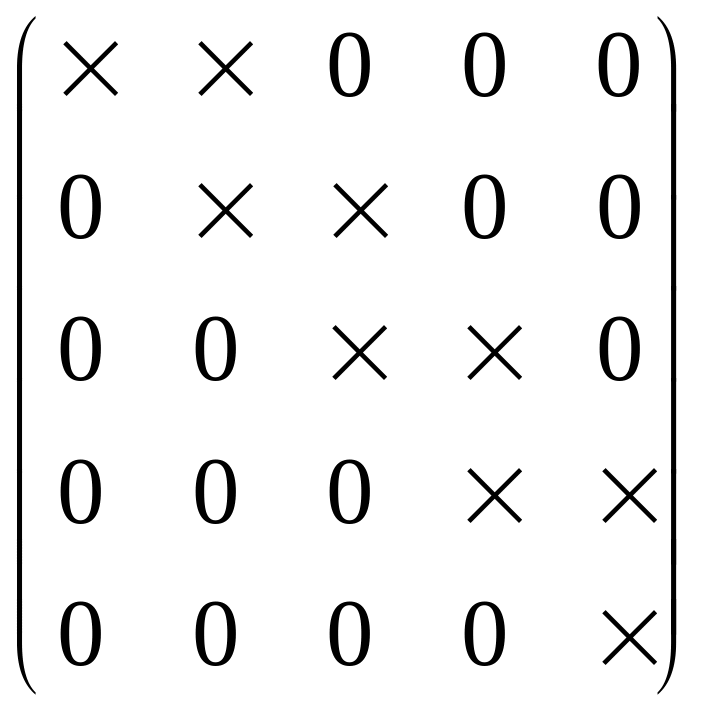(М2)
Пусть система имеет вид
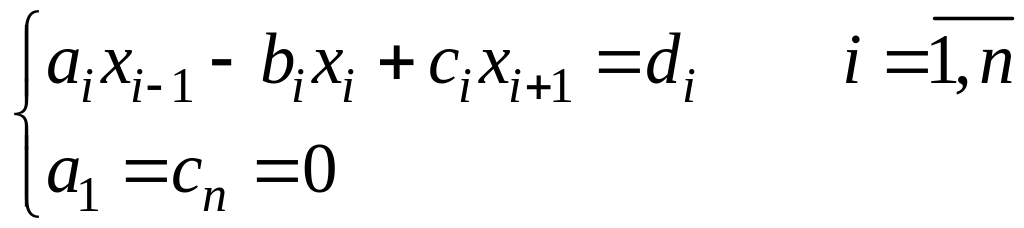(1)
Если
к этой системе применить м-д Гаусса, то
любое уравнение будет связывать
и свободный член.
В методе прогонке решение ищется в виде рекуррентного соотношения (*), которое следует из применимости метода Гаусса
(*)
где
– коэффициенты прогонки.
Нахождение коэффициентов прогонки называется прямым ходом метода прогонки.
Нахождение неизвестных из рекуррентного соотношения (*) – обратный ход метода прогонки