№1 Матрица оның түрлері және оларға қолданылатын амалдар?

m жатық n тік жолдан құрылған кестені mxn өлшемді матрица деп атайды. 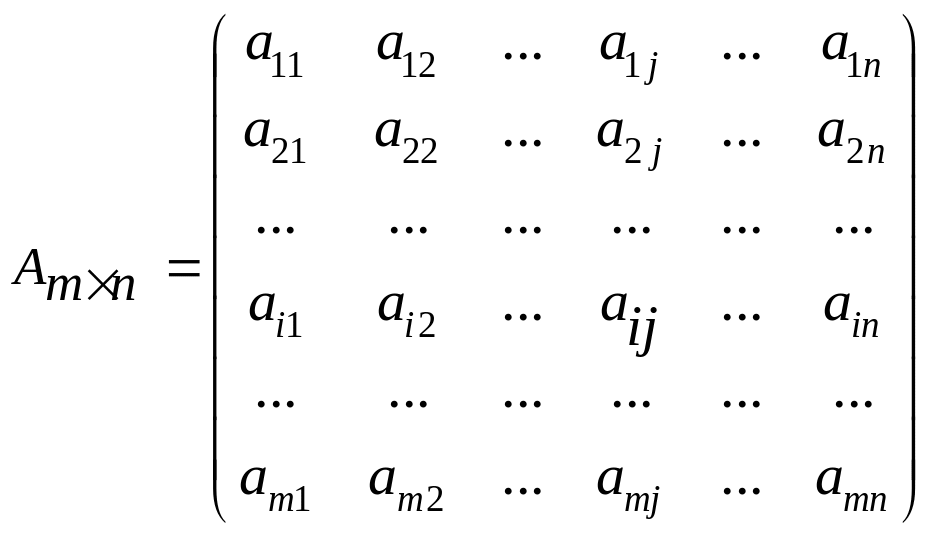Қысқаша жазылуы: Бір ғана жатық жолдан құралған матрицаны жол-матрица, ал бір ғана тік жолдан `құралған матрицаны бағана-матрица деп атайды. Жол матрица мен бағана матрицаны кейде вектор деп те айтады. Жатық жолдар саны мен тік жолдар саны тең болатын матрица квадрат матрица деп аталады. Квадрат матрицаның

элементтері диагоналдық элементтер деп аталады да, матрицаның негізгі диагоналін құрайды. Ал

элементтері қосымша диагоналдық элементтер деп аталады да, матрицаның қосымша диагоналін құрайды.Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады. Диагоналды емес элементтерінің бәрі нолге тең болатын квадрат матрица диагоналды матрица деп аталады. Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді. Барлық элементтері нолге тең матрица нолдік матрица деп аталады.1. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек. 2. Матрицаларды қосу және алу. Өлшемдері бірдей матрицаларды ғана қосуға болады. және 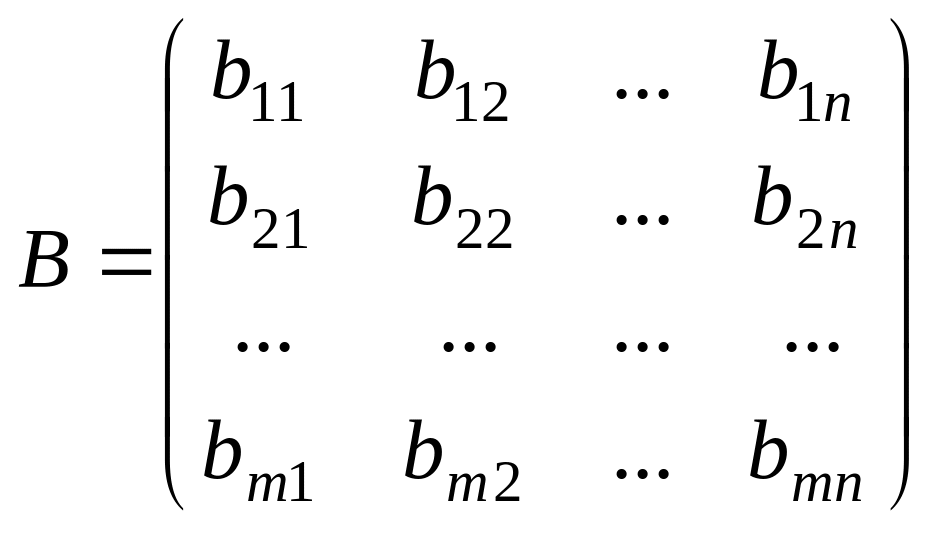матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерін қосындысы болатын, А + В матрицаны айтамыз: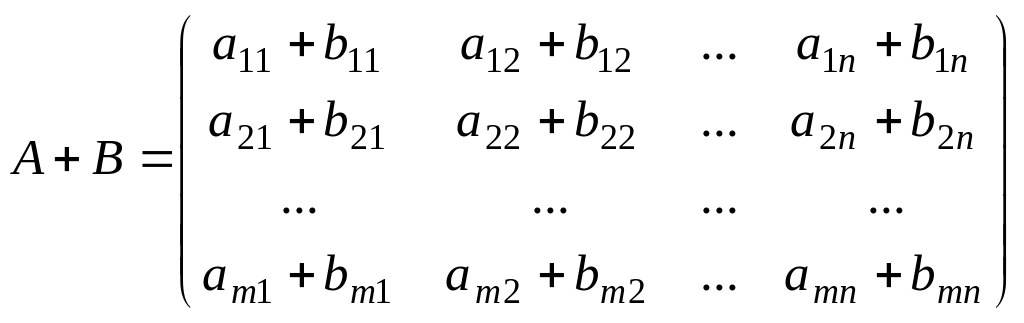 . А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті. 3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Қосу және көбейтудің қасиеттері: 1) A+B=B+A 2) (A+B)+C=A+(B+C) 3) (A+B)= A+ B 4) A(B+C)=AB+AC 5) (A+B)C=AC+BC 6) (AB)=( A)B=A( B) 7) A(BC)=(AB)C

4. Матрицаны транспонерлеу. Қандай да бір А матрицасының жатық жолын сәйкес тік жол етіп жазғаннан пайда болған матрицаны берілген матрицаның транспонерленген матрицасы деп атайды да, деп белгілейді. Берілген матрицаның өлшемі mxn болса, оның транспонерленген матрицасының өлшемі nxm болады.

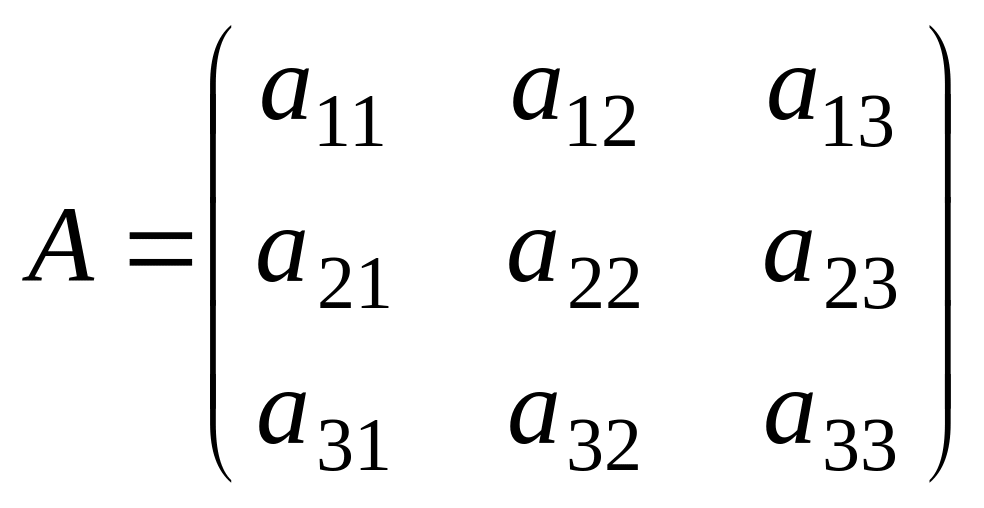№2.квадрат матрица анықтауышы, олардың қасиеттері.. Екінші ретті матрицаның анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады: Үшінші ретті матрицаға үшінші ретті анықтауыш сәйкес келеді: 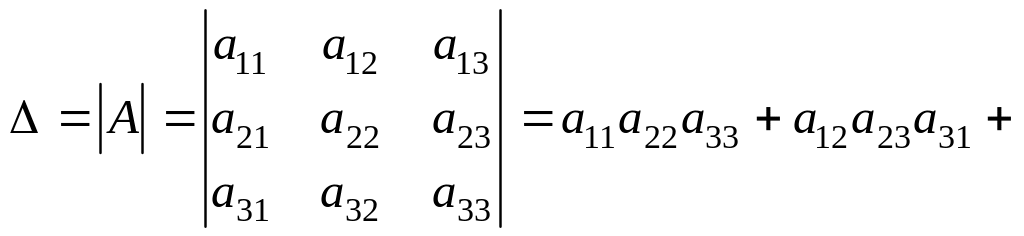Бұл анықтауыштың есептелуін үшбұрыш ережесі немесе Саррус ережесімен оңай есте сақтауға болады. 1-қасиет. Анықтауыштың жатық жолдарын сәкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен, анықтауыш мәні өзгермейді. 2-қас Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. 3-қас Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. 4-қас Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нолге тең. 5-қас Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді.6-қас Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісіне тең.

№3. Минор, алгебралық толықтауыштар.Лаплас теоремасы. n-ретті квадрат матрицаның –жатық жолы мен –тік жолын сызып тастағаннан кейін пайда болған (n–1)-ретті анықтауықты элементінің миноры деп атайды және деп белгілейді. Үшінші ретті марицаның элементінің миноры мынадай екінші ретті анықтауыш: _-элементінің алгебралық толықтауышы деп мынадай санды айтады: Лаплас теоремасы. квадрат матрицаның Δ анықтауышы оның кез келген жол элементтерін сәйкес алгебралық толықтауыштарға көбейтіп қосқанға тең: - бұл анықтауыштың i–жатық жолы бойынша жіктелініп есептелуі. - бұл анықтауыштың j–тік жолы бойынша жіктелініп есептелуі. Лаплас теоремасы n-ретті анықтауыш есептеуді (n-1)-ретті анықтауыш есептеуге келтіріледі.Кез келген n-ретті (n>3) анықтауышты дәрежесін төмендету арқылы екінші ретті анықтауышты есептеуге келтіруге болады.

№4. Кері матрица, матрица рангісі. Анықтауышы нолге тең матрица ерекше, ал нолге тең емес матрица ерекше емес матрица деп аталады. Кез келген сан үшін мына теңдігін қанағаттандыратындай кері сан табылады. А квадрат матрица үшін мына теңдікті қанағаттандыратын матрица А матрицаның кері матрицасы деп аталады. Кері матрицаны мына формуламен табады:

,мұндағы -матрица анықтауышы, ал -берілген матрицаның элементтерінің алгебралық толықтауыштары, i=1,2,…,n; j=1,2,…,n. Кері матрица болуының қажетті және жеткілікті шарты: Матрицаның кері матрицасы болуы үшін ол ерекше емес ( ) матрица болуы қажетті және жеткілікті. Берілген матрицаға кері матрицаны элементар түрлендірулер әдісімен де табуға болады. Бұл әдіс матрицаға элементар түрлендірулер қолдануға сүйенеді. Матрицаның элементар түрлендірулері деп мынадай түрлендірулерді айтамыз:Матрицаны транспонерлеу; Жолдардың орнын алмастыру;Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейту; Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейтіп басқа жолдың сәйкес элементтеріне қосу; Барлық элементі ноль болатын жолды алып тастау.Берілген матрицаның оң жағына бірлік матрица жалғап жазу керек. Сонда өлшемді кеңейтілген матрица пайда болады. В матрицаға А матрицасының орнында бірлік матрица пайда болғанға дейін жатық жолдарына элементар түрлендірулер жасалады. Нәтижесінде бірлік матрицаның орнында кері матрица пайда болады.

mxn өлшемді А матрицаның бірнеше жатық және тік жолдарын сызып тастап k өлшеміді, k min(m,n), квадрат матрица алуға болады. Осы квадрат матрица анықтауышы берілген матрицаның k өлшемді миноры деп аталады. матрицаның k-өлшемді минорлар саны болады.Матрицаның нолге тең емес минорларының ең үлкен реті матрица рангісі деп аталады:r=r(A)= rangA .Тұжырымдар: 1. матрицасының рангісі оның өлшемдерінің кішісінен артпайды:r(A) min(m,n). 2. Барлық элементтері ноль болғанда ғана (нолдік матрица) матрица рангісі ноль болады.3. n–ретті квадрат матрица ерекше емес болғанда матрица рангісі n–ге тең болады. Элементар түрлендірулер матрица рангісін өзгертпейді. Дәлелдеуі. Матрицаға элементар түрлендірулер жүргізгенде оның анықтауышы не өзгермей сақталады, не нолге тең емес санға көбейтіледі. Яғни, оның реті өзгермейді деген сөз. Олай болса, нолден өзгеше минорлардың немесе матрица рангісінің реті де өзгермейді, элементар түрлендірулер жасап, берілген матрицаны барлық диагоналдік элементтері нолден өзгеше болатындай етіп сатылы түрге келтіреміз: , мұндағы r п. Осы шарттың орындалуын матрицаны транстонерлеу арқылы қамтамасыз етуге болады.Сонда матрицаның r–ретті нолден өзге миноры: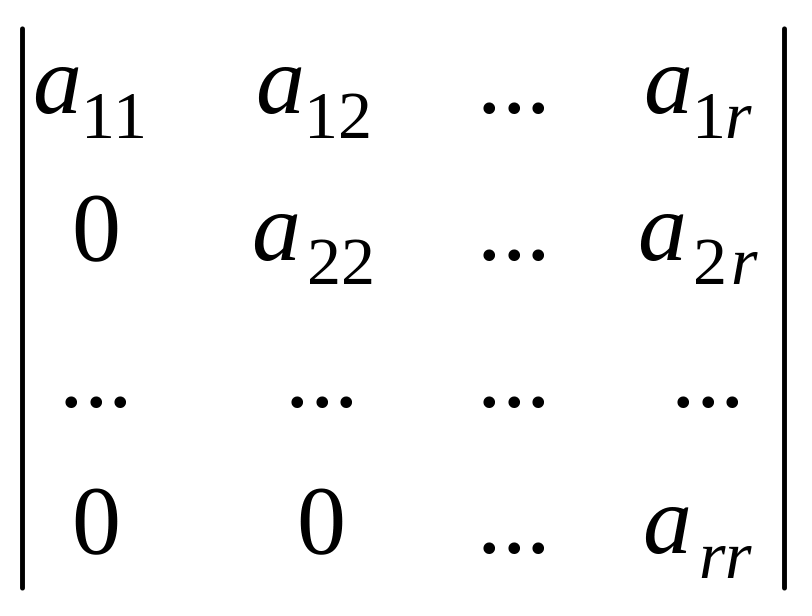 бар болады да, матрица рангісі r-ге тең болады, яғни r(A)=r.

№6. . n белгісізді m теңдеуден тұратын жүйе.Крамер ережесі. n белгісізді m теңдеуден тұратын жүйе деп мынадай жүйені айтады: мұндағы (i=1,2,…,m, j=1,2,…,n) - теңдеу коэффициенттері деп, ал (i=1,2,…,m) - бос мүшелері деп аталады. Теңдеудің қысқаша жазылуы мынадай:

(i=1,2,…,m) жүйенің бос мүшелерінің бәрі нолге тең болса, (i=1,2,…,m) жүйе біртекті жүйе деп аталады. Жүйенің әрбір теңдеуін тепе-теңдікке айналдыратын сандар тізбегі теңдеулер жүйесінің шешімі деп аталады. Осы шартты қанағаттандыратын барлық шешімдер шешімдер жиынын құрады. Жүйенің шешімдер жиынын табу процесін жүйені шешу дейді. жүйенің ең болмағанда бір шешімі болса жүйе үйлесімді, ал шешімі болмаса үйлесімсіз деп аталады. Үйлесімді жүйенің бір ғана шешімі болса, жүйе анықталған, ал шешімі бірден көп болса анықталмаған деп аталады.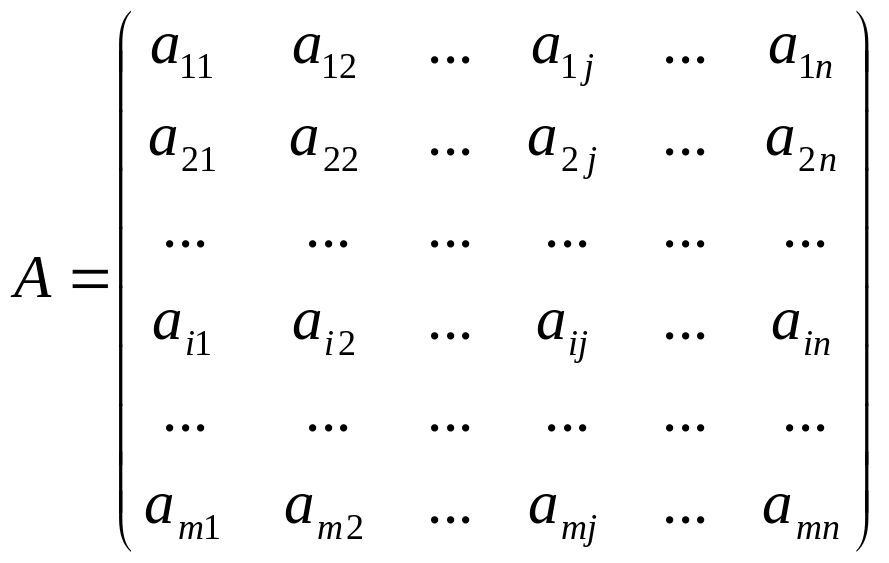 , , 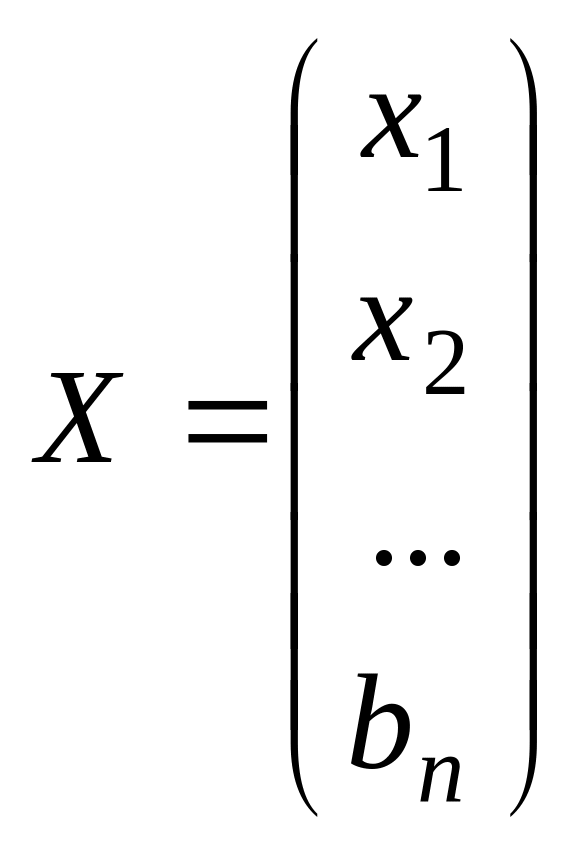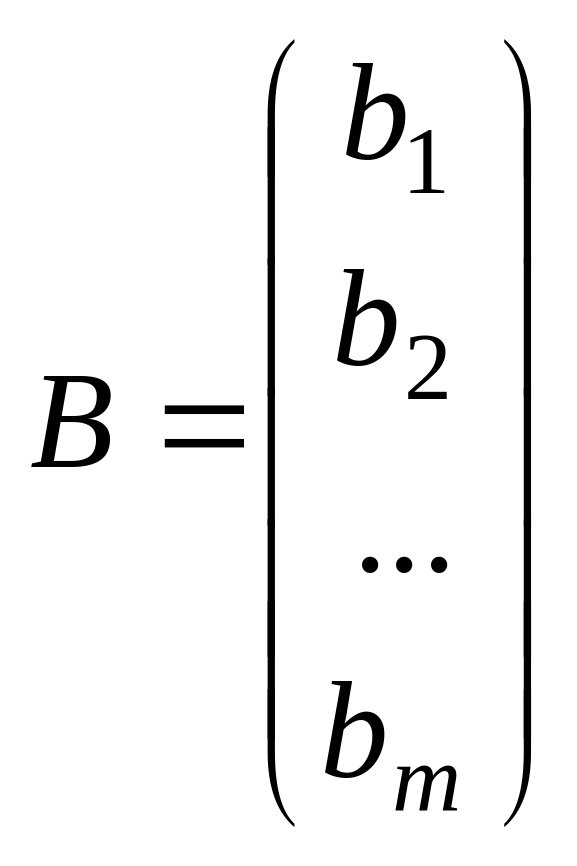А - жүйе коэффициенттерінен құрылған матрица немесе жүйе матрицасы, Х - жүйенің бос мүшелерінен құрылған бағана матрица, В - жүйенің бос мүшелерінен құрылған бағана матрица. Осы белгілеулерді қолданып жүйені былай жазуға болады:АХ=В Егер жүйе матрицасына бос мүшелер матрицасын жалғап жазсақ,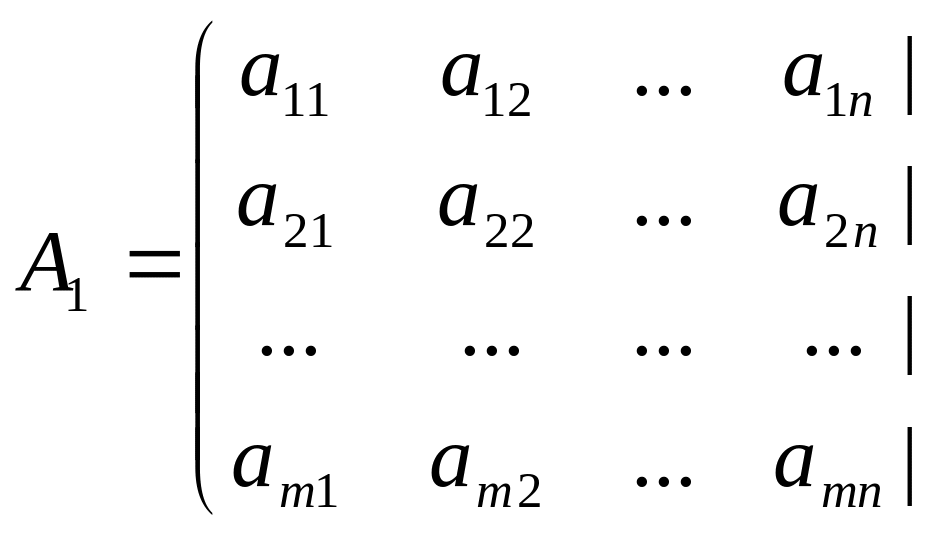

,жүйенің кеңейтілген матрицасын аламыз. Кронеккер-Капелли теоремасы. Егер сызықты теңдеулер жүйесінің негізгі матрицасы мен кеңейтілген матрицасының ранглері тең болса, онда жүйе үйлесімді болады. Жүйе үйлесімді болуы үшін болуы керек. Бұл кезде r жүйе рангісі деп аталады.Үйлесімді жүйенің рангісі жүйедегі белгісіздер санына тең болса (r=n), онда жүйе анықталған болады, ал егер жүйенің рангісі жүйедегі белгісіздер санынан кем болса (r<n), онда жүйе анықталмаған болады. Крамер әдісі- жүйедегі теңдеулер саны мен белгісіздер саны тең болғанда, яғни m=n, қолдануға болады, жүйе түрі мынадай болады: Жүйедегі теңдеулер саны мен белгісіздер саны тең, онда жүйе матрицасы квадрат матрица болады. Сол квадрат матрицаның анықтауышын деп белгілейік:

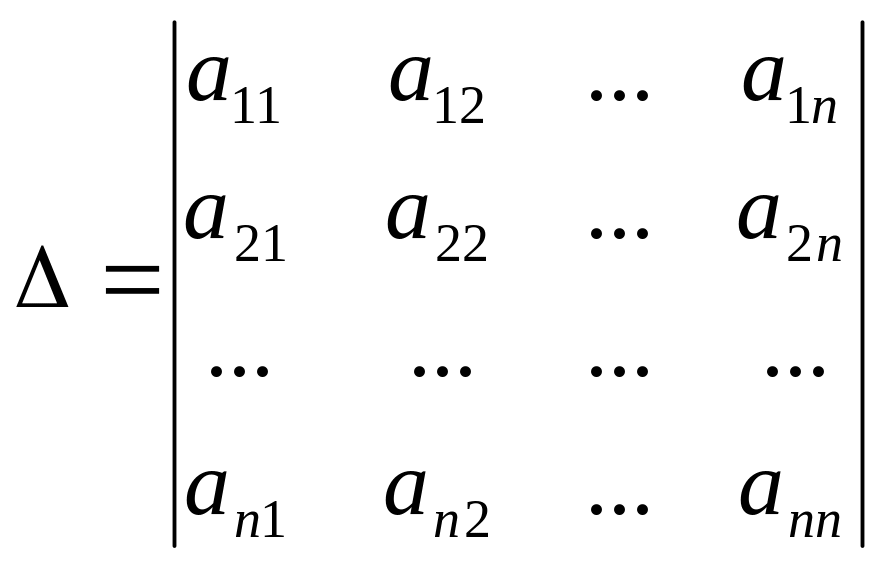
Крамер ережесі. -жүйе анықтауышы, ал - анықтауыштың j-тік жолын бос мүшелермен алмастырғаннан пайда болған анықтауыш болсын. Сонда, егер болса жүйенің жалғыз шешімі бар болады және мынадай формуламен табылады: (i=1,2,…,n)

№7.кері матрица әдісі.и белгісізді м теңдеуден тұратын жүйе Бұл әдіс те жүйедегі теңдеулер саны мен белгісіздер саны тең болғанда, яғни m=n, қолдануға болады. Жүйенің матрицалық жазылуын қарастырайық:АХ=В, мұндағы 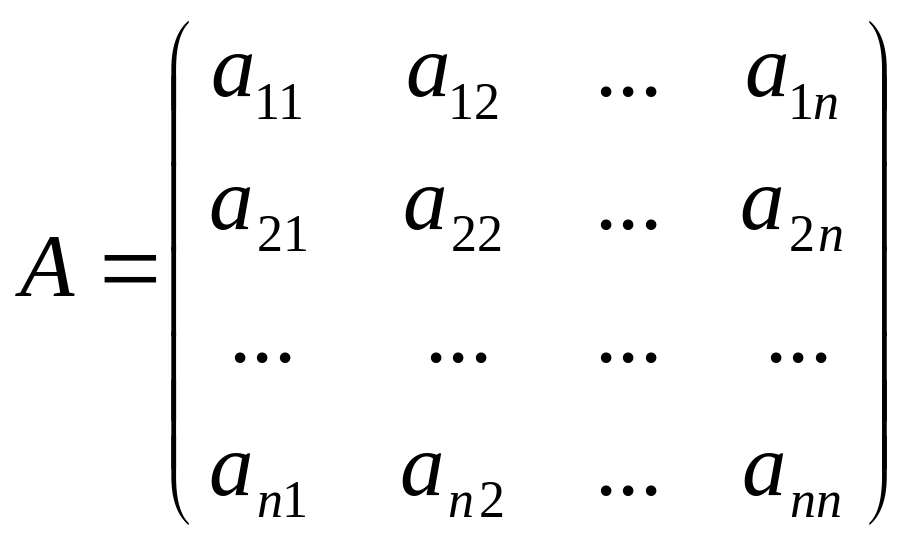, , 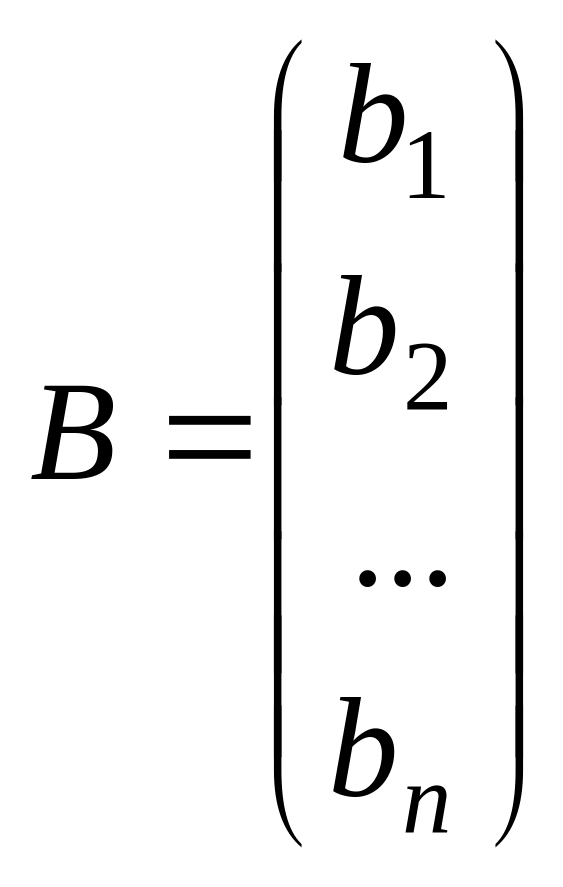. А ерекше емес матрица болсын, яғни матрица анықтауышы нолге тең емес, олай болса әр уақытта кері матрицасы бар болады. Теңдеуді сол жағынан кері матрицаға көб. АХ= В А=E болатындықтан, ЕХ= В, кез келген матрицаның бірлік матрицаға көбейтіндісі сол матрицаның өзіне тең болатындықтан, ЕХ=Х: Х= В. Кері матрицалық әдіс бойынша жүйенің шешімін табу үшін бос мүшелерден құралған матрицаны жүйе матрицасының кері матрицасына көбейту керек екен.

№8. Гаусс әдәсі Гаусс әдісі - жүйедегі айнымалыларды түрлендірулер көмегімен біртіндеп жойып, жүйені сатылы түрге келтіріп, айнымалыларды біртіндеп табатын әдіс. Гаусс түрлендірулері мынадай: Кез келген екі теңдеудің орындарын ауыстырып жазу; Кез келген теңдеудің екі жағын нолден өзге санға көбейту; Қандай да бір теңдеуді нолден өзге санға көбейтіп, басқа теңдеуге сәйкесінше қосу; 0=0 түріндегі теңдеуді сызып тастау. Гаусс түрлендірулерін жүйенің өзіне қолданғаннан гөрі оның кеңейтілген матрицасына қолданған ұтымды болады. Олай болса жүйенің кеңейтілген матрицасын қарастырайық

.Осы мат. түрлендірулер нәтижесінде мынадай түрге келтіреміз: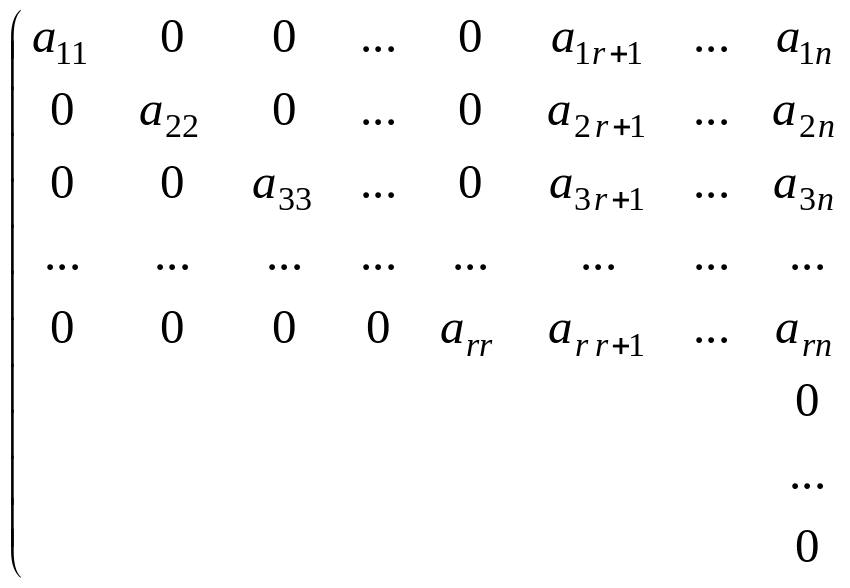

яғни, Соңғы , ..., теңдеулеріндегі , ..., сандарының ең болмағанда біреуі нөлден өзгеше болса, онда берілген теңдеулер жүйесі үйлесімсіз, ал бәрі нолге тең болса жүйе үйлесімді болады. Жүйенің рангісі жүйедегі белгісіздер санынан кем болса, онда жүйе анықталмаған болатыны жоғарыда айтылған. Жүйе үйлесімді және r<n болсын. Егер коэффициенттерінен құрылған анықтауыш нолден өзгеше болса, онда айнымалыларды базистік (негізгі) айнымалылар деп, ал басқа n-r айнымалыларды еркін (негізгі емес) айнымалылар деп атайды. Еркін айнымалылары нолге тең болған кездегі шешім базистік шешім деп аталады. Базистік шешімдер саны -ден артпайды.

№ 11. Аналитикалық геометрияның қарапайым есептері. 1. Екі нүкте ара қашықтығы. Жазықтықта және екі нүкте берілсін. Осы екі нүкте ара қашықтығын, немесе АВ кесіндісінің ұзындығын, мына формуламен есептейді:

.

2. Кесіндіні берілген қатынаста бөлу. Жазықтықта және екі нүкте берілсін. АВ кесіндісін АМ:МВ= болатындай қатынаспен бөлетін М(х,у) нүктесінің координаталары мынадай формуламен есептелінеді: . Дербес жағдайда, АВ кесіндісін тең екіге бөлу керек болса, яғни =1:1=1, формула былай түрленеді:

, .

3. Үшбұрыш ауданы. Жазықтықта төбелері , , болатын үшбұрыш ауданы мынадай формуламен есептелінеді: .

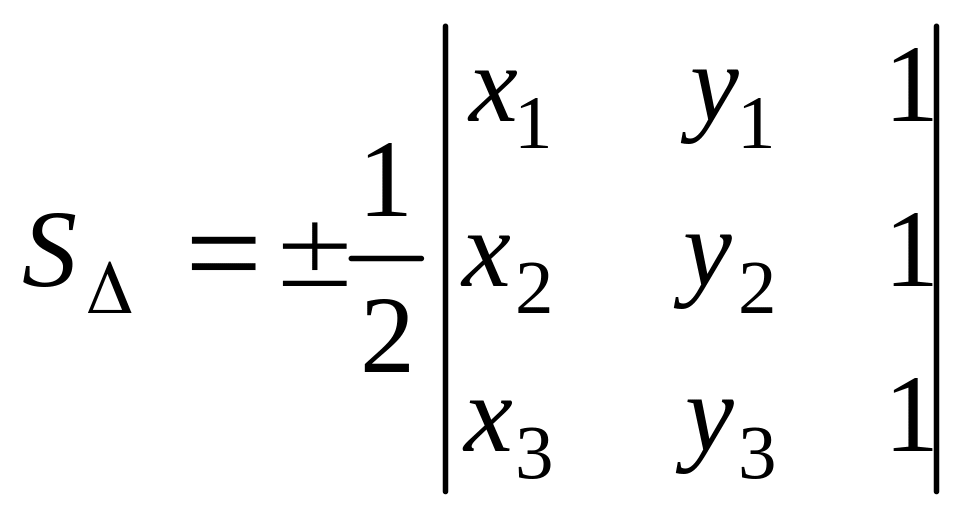№12. Жазықтықтағы түзудің теңдеулері. Берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуі. Көп жағдайда түзу теңдеуін оның бойында жатқан белгілі нүкте мен k бұрыштық коэффициенті арқылы жазу керек болады (5-сурет).

y=kx+b, мұндағы b әзірше белгісіз. Түзу нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₁=kx₁+b. Осы теңдіктен белгісіз b табылады, b = y₁ - kx_1. Табылған мәнді теңдеудегі орнына қойып, берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуін аламыз: y =k(x – x₁)+ y₁ Егер (4) теңдеудегі k ерікті мән қабылдаса, онда теңдеу нүктесі арқылы өтетін түзулер шоғының теңдеуін анықтайды (6-сурет). Берілген екі нүкте арқылы өткен түзу теңдеуі.

және нүктелері

берілсін. АВ түзуінің теңдеуін жазу үшін А нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз: y =k(x – x₁)+ y_1. АВ түзуі нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₂ =k(x₂ – x₁)+ y_1. Осы теңдіктен белгісіз k табылады, . Табылған мәнді теңдеудегі орнына қойып, берілген екі нүкте арқылы өткен түзу теңдеуін аламыз:

Түзудің “кесіндідегі” теңдеуі. Түзу Ох осінен а-ға тең, Оу осінен b-ға тең кесінді қиып өтсін (8-сурет). Түзу А(а;0) және В(0;b) нүктелері арқылы өтеді деп, Сонда түзу теңдеуі мынадай түрде

жазылады:

Енді ықшамдасақ, түзудің “кесіндідегі” теңдеуін аламыз:

Екі түзу арасындағы бұрыш. 9-Суреттен көрініп тұрғандай . Осыдан немесе формула берілген екі түзу арасындағы бұрышты анықтайды. Ал екінші бұрыш тең болады.

№13.Екі түзудің параллелдік және перпендикулярлық шарты. Нүктеден түзуге дейінгі қашықтық.

Егер екі түзу параллель болса, онда =0 болады да tg =0, яғни: k₂ – k₁ = 0. Осыдан екі түзудің параллелдік шарты шығады: k₂ = k₁ , яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше. Егер екі түзу перпендикуляр болса, онда болады да, , . Осыдан екі түзудің перпендикулярлық шарты шығады: k₂ = , яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше. Нүктеден түзуге дейінгі қашықтық. Тік бұрышты координаталар жүйесінде қандай да бір түзу Ах+Ву+С=0 және түзуден тыс жатқан нүкте М(х₀,у₀) берілсін

Нүктеден түзуге дейінгі қашықтық деп нүктеден түзуге түсірілген перпендикуляр ұзындығын айтамыз. Суретте ол d=MN. Осы ара қашықтықты табу үшін: а) Берілген түзуге перпендикуляр және М(х₀,у₀) нүктесі арқылы өтетін түзу теңдеуін тауып аламыз; б) Берілген түзу мен MN түзулерінің теңдеуін жүйе етіп шешіп, олардың қилысу нүктесі N табамыз; в) екі нүктенің ара қашықтығын есептейтін формула көмегімен d=MN ара қашықтықты есептейміз. Нәтижесінде мынадай формула алынады:

№14. векторлық кеңістік. Векторлардың сызықты тәуелділігі ж\е сызықты тәуелсіздігі. Мысал келтіру.

Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды белгілеудің немесе , кейде тек қалың сызықпен АВ түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( = , , а). векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады, = және ұзындығы нолге тең. Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады. және векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады: және векторларының - айырымы деп -ға қосқанда векторы алынатын векторын айтады. векторының санға көбейтіндісі деп ұзындығы болатын, бағыты >0 болғанда векторымен бағыттас, <0 болғанда векторымен қарама-қарсы бағытта болатын векторын айтады. Суретте, = 2, = -1. Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусына көбейтіндісіне тең шаманы айтады:

Тік бұрышты декарт координаталар жүйесінде векторының басы мен соңының координаталары белгілі болсын және . Сонда векторын координаталары арқылы былай жазуға болады:

=

векторының басы координаталар басымен беттесетіндей етіп өз-өзіне параллель көшірсек, онда векторының координатасы вектордың соңының координаталарымен бірдей болатынын аңғару қиын емес.Жазықтықта вектордың координатасын екі сан анықтаса, айталық , кеңістікте үш сан анытайды, . Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең:

және векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады:

Ал векторын санға көбейту мынадай түрде анықталады және векторларының скаляр көбейтіндісі мынадай:

Енді векторлық кеңістік ұғымына көшейік. Элементтері x, y, z, … болатын қандай да бір R жиын қарастырайық. Осы жиынның кез келген x және y элементтері үшін қосу x + y амалы мен қандай да бір х элементі және нақты сан үшін көбейту х амалы орындалсын. Анықтама. R жиынның элементтерін қосу және элементін нақты санға көбейту амалдары төмендегідей шарттарды қанағаттандырса, R жиын векторлық (сызықтық) кеңістік деп, ал элементтерін векторлар деп атайды:

1. x+y=y+x;

2. (x+y)+z=x+(y+z);

3. Кез келген x 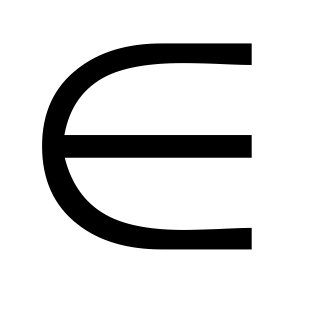R үшін 0 R (нол-элемент) табылады да, мынадай қатынас орындалады: x+0=x;

4. Кез келген x R үшін -х R (қарама-қарсы элемент) табылады да, мынадай қатынас орындалады: x+(-x)=0;

5. x=x;

6. ( x)=( )x;

7. (x+y)= x+ y

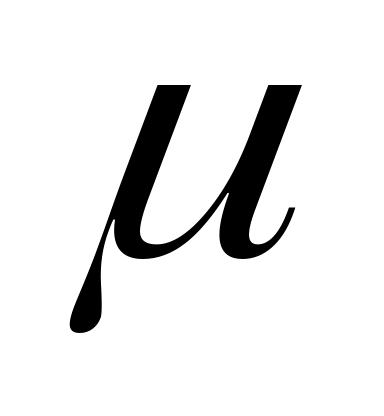8. ( + )x= x+ x.

x және y векторларының айырмасы деп х векторы мен –1у векторларының қосындысын айтамыз: x-y=x+(-1)y Векторлық кеңістіктің анықтамасынан кез келген х векторды 0 нақты санына көбейткенде пайда болатын жалғыз 0 - ноль вектордың бар болатындығы; әрбір х вектор үшін осы векторды (-1) санына көбейткенде пайда болатын жалғыз қарама-қарсы ( –х) вектордың бар болатындығы шығады.

15. Сызықты тәуелді және сызықты тәуелсіз векторлар

R сызықты кеңістіктің векторлары x, y, z, …, u болсын. Мынадай

v= x+ y+ z+…+ u

теңдікпен анықталған v векторы осы кеңістікте жатады, мұндағы -нақты сандар. Осы v векторды x, y, z, …, u векторларының сызықты комбинациясы деп атайды.

Айталық x, y, z, …, u векторларының сызықты комбинациясы 0 ноль вектор болсын, яғни

x+ y+ z+…+ u= 0. (1)

Анықтама. (1) теңдік барлық = = =…= =0 болған кезде ғана орындалса х, y, z, …, u векторлары сызықты тәуелсіз деп аталады. Ал егер (1) теңдік , , ,…, сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса х, y, z, …, u векторлары сызықты тәуелді деп аталады.

Мынадай тұжырымның дұрыстығына көз жеткізу қиын емес: Егер x, y, z, …, u векторлар сызықты тәуелді болса, онда бұл векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктеледі. Және керісінше, Егер x, y, z, …, u векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктелсе, онда бұл векторлар сызықты тәуелді болады.

Жазықтықтағы коллинеар емес екі вектор сызықты тәуелсіз векторға мысал болады. Шынында да, жазықтықтағы және векторлары үшін (1) теңдік

+ =0

тек = =0 болғанда ғана орындалады. Ал, олай демесек, мысалы болса, онда =- болып, пен векторларының коллинеарлығын білдірген болар еді. Ал бірақ жазықтықтағы кез келген үш вектор сызықты тәуелді болады.

Векторлық кеңістіктің қасиеттері:

1. Егер x, y, z, …, u векторларының ішінде ноль-вектор бар болса, онда бұл векторлар сызықты тәуелді болады. Шынында да, егер, мысалы, x=0 болса, онда (1) теңдік

=1, = =…= =0 болғанда орындалады.

2. Егер x, y, z, …, u векторларының қандай да бір бөлігі сызықты тәуелді болса, онда бұл векторлардың бәрі сызықты тәуелді болады. Шынында да, мысалы, y, z, …, u векторлары сызықты тәуелді болсын десек y+ z+…+ u=0 теңдік , ,…, сандарының бәрі бір мезгілде нолге тең болмағанда орындалып тұр деген сөз. Олай болса бұл теңдік сол , ,…, сандары және =0 санымен де орындалады.

16.Кеңістіктегі базис ұғымы. Векторды базис бойынша жіктеу. Анықтама. Егер R сызықты кеңістікте n сызықты тәуелсіз вектор бар болып, ал осы кеңістіктің кез келген n+1 векторы сызықты тәуелді болса, онда R кеңістікті n өлшемді деп атайды. Кейде кеңістік өлшемі n-ге тең дейді де, dim(R)=n деп немесе Rⁿ деп жазады.

Анықтама. п өлшемді векторлық кеңістіктің п сызықты тәуелсіз векторларының жиыны базис деп аталады.

Мынадай тұжырымдар дұрыс болады:

1. Егер қандай да бір векторлар базис құрса, онда осы векторлардың координаталарынан құрылған анықтауыш нолден өзгеше болады.

2. п өлшемді векторлық кеңістіктің әр бір векторы базистік векторлардың сызықты комбинациясы арқылы жазылады және бұл жазу жалғыз болады. Сонда, егер - кеңістіктің базисі болса, онда кез келген x R векторы жалғыз түрде былай жазылады:

.

Демек базисінде х векторы сандарымен жалғыз түрде анықталады. сандар х векторының осы базистегі координаталары деп аталады.

Мысал. x=(1;3;0), y=(-1;2;1), z=(1;-1;2) векторлары базис құра ма? Егер құрса u=(2;0;1) векторын (x,y,z) базисі бойынша жікте (яғни, u векторын x, y, z векторларының сызықты комбинациясы арқылы жазу керек).Шешуі. Бірінші тұжырым бойынша x, y, z векторлары базис құрса, онда осы векторлардың координаталарынан құрылған анықтауыш нолден өзгеше болуы керек:

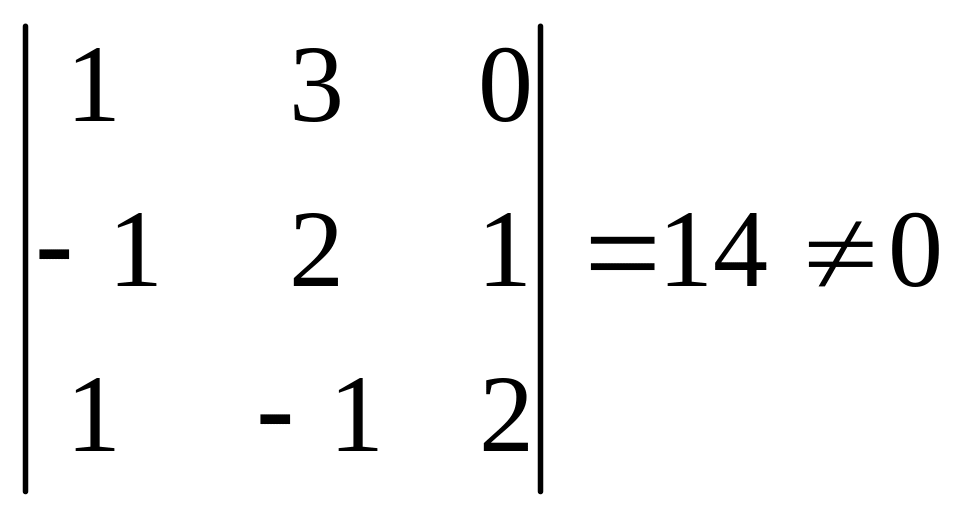
Демек, x, y, z векторлары базис құрады екен.

Екінші тұжырым бойынша u векторы (x,y,z) базисте жіктеледі және ол жіктелу жалғыз болады:

.

x, y, z, u векторларын бағана түрінде жазып, теңдікті ашып жазайық:

+ + =

Есеп мынадай жүйені шешуге келтірілді:

Осы жүйені шешіп u векторының (x, y, z) базисіндегі ( , , ) координаталарын табамыз. Үш белгісізді үш теңдеуден тұрған жүйені жүйе шешудің кез келген әдісімен шешуге болады. Сонда мынадай жалғыз шешім аламыз:

, , .

Сонымен, .

17.Функция ұғымы. Функция шегі. Функция немесе функциялық тәуелділік ұғымы түрлі шамалар, экономикалық көрсеткіштер арасындағы байланыстарды моделдейтін математиканың маңызды ұғымы.

Анықтама. Х жиынының әрбір х элементіне ( ) белгілі бір заң немесе ереже бойынша У жиынының у элементі сәйкес қойылса, онда Х жиынында функция берілген деп атайды.

х және у шамаларының арасындағы функциялық тәуелділікті y=f(x) деп белгілейді, мұндағы х - аргумент(тәуелсіз айнымалы), у – функция(тәуелді айнымалы), f – ереже немесе заң.

Берілген функция анықталатын х аргументтерінің жиынын функцияның анықталу облысы деп, ал сәйкес у айнымалылардың жиынын функцияның мәндер жиыны деп атайды. Әдетте анықталу облысын D(f) деп, ал мәндер жиынын E(f) деп белгілейді.

Функция түрлі тәсілдермен берілуі мүмкін. Ең көп және маңызды берілу түрлері: аналитикалық(формула түрінде), кестелік және графиктік.

Енді функция шегінің анықтамасына көшейік. y=f(х) функциясы қандай да бір х₀ нүкте маңайында анықталған болсын.

Анықтама. Егер алдын ала берілген, мейілінше аз санына саны табылып, шартын қанағаттандыратын барлық х үшін теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х₀-ге ұмтылғандағы шегі деп аталады да, былай жазылады:

.

Анықтамадағы теңсіздікті ашсақ, мынадай қос теңсіздік аламыз:

.

интервалды нүктесінің -маңайы дейді.

Сол сияқты теңсіздікті ашсақ:

.

интервалды А нүктесінің -маңайы дейді.

Алдын ала берілген, санына саны табылып, аргумент мәндері нүктесінің -маңайына тиісті болғанда функцияның сәйкес мәндері А нүктесінің -маңайында жатса, А саны f(x) функциясының х аргумент х₀-ге ұмтылғандағы шегі деп аталады.

Функция шегінің қасиеттері. Айталық және функцияларының жағдайда және шектері бар болсын.

1. Екі функцияның алгебралық қосындысының шегі шектердің алгебралық қосындысына тең болады, яғни

= .

2. Екі функцияның көбейтіндісінің шегі шектердің көбейтіндісіне тең болады, яғни

= .

№18.тамаша екі шек және салдары. Егер алдын ала берілген, мейілінше аз санына саны табылып, шартын қанағаттандыратын барлық х үшін теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х₀-ге ұмтылғандағы шегі деп аталады да, былай жазылады: . теңсіздікті ашсақ, мынадай қос теңсіздік аламыз: . интервалды нүктесінің -маңайы дейді. Сол сияқты теңсіздікті ашсақ: . интервалды А нүктесінің -маңайы дейді. функциясы x=0 нүктеде анықталмаған, бірақ жағдайда шегі бар және Осы шекті бірінші тамаша шек деп атайды.Бірінші тамаша шек салдары: 1) , 2) , 3) . Мысалдар:

. ж\е .

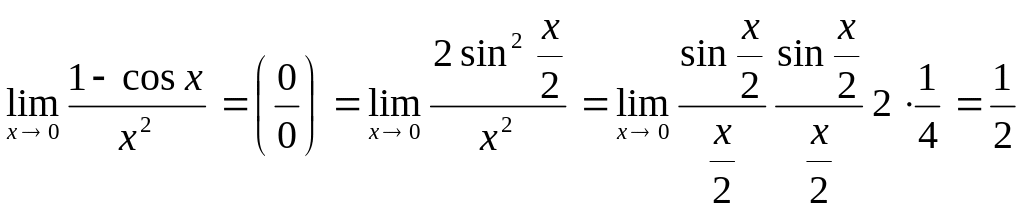
функциясының жағдайда шегі бар және Осы шекті екінші тамаша шек деп атайды. Мұндағы иррационал саны Эйлер саны екені белгілі.Екінші тамаша шек салдары:1) , a=e болғанда ;2) , a=e болғанда ; 3)

_{№19. Ақырсыз аз шама қаситеі. Ақырсыз аздарды салыстыру.} функциясының жағдайда шегі ноль болса, яғни , онда функциясы жағдайда ақырсыз аз функция деп аталады. “ ” тілінде былай да айтуға болады: Кез келген үшін саны табылып, теңсіздігін қанағаттандыратын барлық х-тер үшін теңсіздігі орындалса, функциясы жағдайда ақырсыз аз функция деп аталады.Ақырсыз аз функция қасиеттері. 1.Егер функциясының жағдайда А шегі бар болса, онда функциясын осы А саны мен жағдайда ақырсыз аз болатын функция қосындысы түрінде жазуға болады, яғни . 2.Ақырсыз аз функцияның шенелген функцияға (сонмен қатар, тұрақтыға, басқа ақырсыз азға) көбейтіндісі ақырсыз аз функция болады. 3.Ақырсыз аз функцияның шегі нолден өзге функцияға қатынасы ақырсыз аз функция болады. функциясының жағдайда шегі шексіздік болса, яғни , онда функциясы жағдайда ақырсыз үлкен функция деп аталады. Ақырсыз аз функция мен ақырсыз үлкен функция арасында мынадай байланыс бар: Егер функциясы жағдайда ақырсыз аз болса, функциясы жағдайда ақырсыз үлкен болады. Ақырсыз аз функциялар нолге әртүрлі жылдамдықпен жақындайды. Көптеген жағдайда ақырсыз аздардың нолге ұмтылу жылдамдығын анықтау үшін оларды өзара салыстыру керек болады. Салыстыру үшін олардың қатынасының жағдайдағы шегін қарастырады. және жағдайда ақырсыз аз функциялар және болсын. Онда, егер 1) болса -ға қарағанда жоғары ретті ақырсыз аз деп;2) болса мен бірдей ретті ақырсыз аз деп;3) болса мен эквивалентті ақырсыз аз деп аталады.

№21 Функция үзіліссіздігі, қасиеттері. Үзіліс нүктелері, үзіліс түрлері.

функциясының жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни , функция нүктесінде үзіліссіз деп аталады. . Сонда функция үзіліссіздігінің анықтамасын былай да айтуға болады: Берілген нүктеде аргументтің ақырсыз аз өсімшесіне функцияның да ақырсыз аз өсімшесі сәйкес келсе, яғни функция нүктесінде үзіліссіз деп аталады. функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.Үзіліссіз функция қасиеттері.1. функциясы нүктесінде үзіліссіз, ал функциясы нүктесінде үзіліссіз болса, күрделі функциясы нүктесінде үзіліссіз болады және .

2.Нүктеде үзіліссіз функциялардың алгебралық қосындысы, көбейтіндісі және қатынасы (бөліміндегі функция нолден өзге болғанда) үзіліссіз функция болады. функциясының жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни , функция нүктесінде үзілісті функция деп, ал нүктені функцияның үзіліс нүктесі деп атайды және , онда деп жазады, ал осы жағдайдағы шекті функцияның сол жақты шегі деп атайды. Дәл осылайша функцияның оң жақты шегі де анықталады. Функцияның сол жақты және оң жақты шектерін біржақты шектер дейді.Үзіліс түрлерін ажыратайық. Функцияның нүктесінде өз-ара тең емес ақырлы біржақты шектері бар болса, нүктесі функцияның І-текті үзіліс нүктесі деп аталады. Кейде оны ақырлы секіріс деп (10а-сурет) атайды. Функцияның нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса, нүктесі функцияның ІІ-текті үзіліс нүктесі деп аталады.

№22 Функция туындысы. Үзіліссіздік пен дифференциалдану арасындағы байланыс

Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған кездегі шегі функция туындысы деп аталады. Әдетте оны немесе деп белгілейді: Функцияның туындысын алуды – функцияны дифференциалдау дейді. (а;в) интервалының әрбір нүктесінде туындысы бар функцияны сол интервалда дифференциалданады дейді. Мына тұжырым дұрыс болады: Егер f(x) функцисы х₀ нүктеде дифференциалданса, онда функция х₀ нүктеде үзіліссіз болады. Бірақ осыған кері тұжырым дұрыс бола бермейді. Мысалы, y=|x| функциясы x=0 нүктеде үзіліссіз. Бірақ оның x=0 нүктедегі туындысы болмайды. Шынында да, егер бар болса, туындыны мына формуламен табар едік: .Ал x=0 нүктеде болғандықтан қатынастың шегі болмайды. Шек болмаса туындысы да жоқ.

_№23 Дифференциалдаудың негізгі ережелері. Күрделі, кері функциялар туындысы.

Дифференциалдау ережелері. u=u(x) және v=v(x) функциялардың әрқайсысы берілгенх нүктесінде дифференциалданатын болса, онда бұл функциялардың қосындысы(айырымы), көбейтіндісі және қатынасы (v(x) 0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:

1)

2) , C=const

3)

4) .

5. f(u(x)) күрделі функция туындысы:

.

5. y=f(x) функциясына кері функция (x=f ^{- 1}(y)) туындысы:

.

5. Айқын емес түрде берілген функция, F(x,y)=0, туындысы:

.

5. Дәрежелі-көрсеткіштік 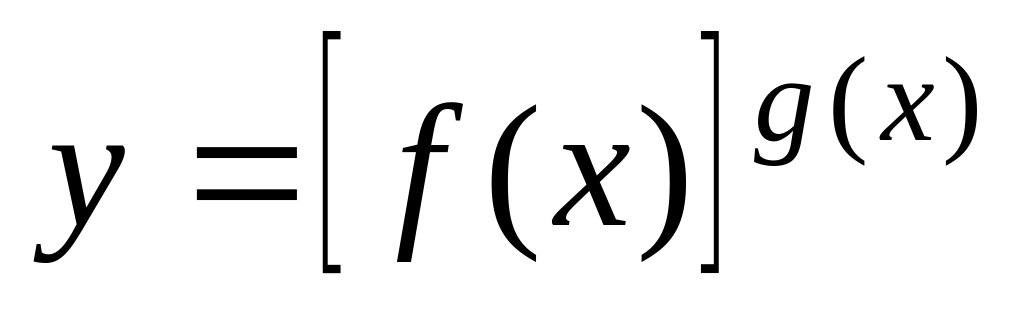функция туындысы. Алдымен берілген теңдеудің екі жағын логарифмдейік,

.

Екі жағынан туынды аламыз,

.

Сонымен,

.

9) Жоғары ретті туынды. туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да, деп белгіленеді. Сонымен,

.

Осылайша 3-ретті, т.с.с. n–ретті туындыларды анықтауға болады,

, …, .

24.Логарифмдік дифференциалдау. Жоғары ретті туынды.

Жоғары ретті туынды. туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да, деп белгіленеді. Сонымен,

.

Осылайша 3-ретті, т.с.с. n–ретті туындыларды анықтауға болады,

, …, .

25. Функция дифференциалы. Жуықтап есептеулердегі қолданысы.

Функция өсімшесінің сызықты бөлігі функция дифференциалы деп аталады да, dy деп белгіленеді. Сонымен, y=x функциясының дифференциалын табайық: . Демек аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз: Егер аргумент өсімшесі абсолют шамасы бойынша аз шама болса, онда функция өсімшесі мен дифференциалы жуық шамамен тең болады, яғни . Түрлендірейік, . Осыдан, формуламен функцияның мәнін жуықтап есептейді. Неғұрлым аз болса, соғұрлым формула дәлірек болады.

№26. Лопиталь ережесі. f(x) және g(x) функциялары ( ) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады: . Мыс: .Бұл мысалда Лопиталь ережесін бірден қолдануға келмейді. Сондықтан, алгебралық түрлендіру көмегімен түріндегі анықталмағандықты немесе түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х² бөлімнің бөліміне түсірдік.

№29. Функцияның экстремумның қажетті және жеткілікті шарты. Экстремумның бар болуының қажетті шартын Ферма теоремасы береді.

Ферма теоремасы. х₀ нүктесі y=f(x) функциясының экстремум нүктесі болып және осы нүктедегі функция туындысы бар болса, онда =0.

Бұл теореманың геометриялық мағнасы: теорема шартын қанағаттандыратын нүктеде функция графигіне жүргізілген жанама абсцисса осіне параллель болады.

Анықтама. Туындысы нолге айналатын не туындысы болмайтын нүктелер функцияның күдікті нүктелері (кейде І-текті күдікті нүктелер) деп аталады.

х₀ нүктесінің - маңайы табылып, (х₀- х₀+ ), осы маңайдағы барлық х х₀ үшін f(x)>f(х₀) теңсіздігі орындалса, х₀ нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х₀) теңсіздік орындалса, х₀ нүктесі f(x) функциясының максимум нүктесі деп аталады. Функцияның минимум және максимум нүктелерін экстремум нүктелері деп атайды. Осы нүктелердегі функция мәндерін функция экстремумдары дейді. Экстремумның бірінші жеткілікті шарты. y=f(x) функциясы х₀ нүктесінде үзіліссіз және қандай да бір - маңайында функция туындысы бар болсын (х₀ нүктесінде туынды болмауы мүмкін). Онда, 1.егер х аргумент х₀ нүкте арқылы өткенде таңбасын оңнан теріске өзгертсе, онда х₀ нүкте максимум нүктесі болады;2.егер х аргумент х₀ нүкте арқылы өткенде таңбасын терістен оңға өзгертсе, онда х₀ нүкте минимум нүктесі болады;3.егер х аргумент х₀ нүкте арқылы өткенде таңбасын өзгертпесе, онда х₀ нүкте экстремум нүктесі емес. Экстремумның екінші жеткілікті шарты. y=f(x) функциясы х₀ нүктесінде үзіліссіз және қандай да бір - маңайында екі рет дифференциалдансын. Сонымен қатар болса, онда 1.егер болса, онда х₀ нүкте f(x) функциясының максимум нүктесі болады;2.егер болса, онда х₀ нүкте f(x) функциясының минимум нүктесі болады.

№30 Функция графигінің дөңестігі, иілу нүктелері

y=f(x) функция графигі (а,в) интервалының кез келген нүктесінде жүргізілген жанамадан төмен жатса, онда функция дөңес (дөңестігі жоғары қараған) деп, ал жанамадан жоғары жатса, онда функция ойыс (дөңестігі төмен қараған) деп аталады. Функция графигінің дөңес және ойыс бөліктерін бөліп тұратын нүктені функцияның иілу нүктесі деп атайды. Функция дөңестігінің жеткілікті шарты. (а,в) интервалында y=f(x) функциясының екінші ретті туындысы теріс таңбалы болса, функция графигі осы аралықта дөңес, ал екінші туындысы оң таңбалы болса, функция графигі осы аралықта ойыс болады. Иілу нүктесі бар болуының қажетті шарты. (а,в) интервалында екі рет дифференциалданатын y=f(x) функциясының (x₀, f(x₀)) нүктесі иілу нүктесі болса, онда .Екінші туындысы нолге айналатын не болмайтын нүктелер функцияның ІІ-текті күдікті нүктелері деп аталады. Иілу нүктесі бар болуының жеткілікті шарты. (а,в) интервалында екі рет дифференциалданатын y=f(x) функциясының екінші туындысы х аргумент х₀ нүкте арқылы өткенде таңбасын өзгертсе, онда (x₀, f(x₀)) нүктесі функцияның иілу нүктесі болады.

№31. Асиптоталар. Функцияны зерттеп, графигін салудың жалпы сүлбесі.

.Егер y=f(x) функциясы үшін ж\ шектерінің ең болмағанда біреуі шексіздікке тең болса, онда функция графигінің тік асимптотасы деп аталады. у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы деп аталады, егер функцияға тиісті қандай да бір М нүкте координат басынан алыстаған сайын түзуге шексіз жақындаса Көлбеу асимптотаның дербес жағдайы (k=0) горизонталь асимптота болады: y=b. у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы болуы үшін мынадай шектердің бар болуы қажетті және жеткілікті: , .Функцияны зерттеп оның графигін салуды мынадай ретпен жүргізген жөн:

1. Функцияның анықталу облысын табу;

2. функцияны жұп, тақтылыққа зерттеу;

3. функцияны периодтылыққа зерттеу;

4. функцияны үзіліссіздікке зерттеп, үзіліс нүктелерін табу;

5. күдікті нүктелерін табу;

6. монотонды аралығы мен экстремумдарын табу;

7. ойыс, дөңес аралықтарын, иілу нүктелерін табу;

8. функция графигінің асимптоталарын табу;

9. функция графигінің координаталар осімен қилысу нүктелерін;

10. зерттеулерге сүйеніп график салу.

№32. Интеграл қасиеттері. Интегралдар кестесі.

. Анықталған интеграл ж\е оның касиеттері. y=f(x) функциясының интегралдық қосындысының жағдайдағы шегі функцияның [a;b] аралығындағы анықталған интегралы деп аталады және деп белгіленеді. Сонымен, мұндағы а және b сандары интегралдың сәйкес төменгі және жоғарғы шектері деп аталады. Анықталған интеграл қасиеттері: 1.Тұрақтыны шек таңбасы алдына шығаруға болады: . 2.Екі функцияның алгебралық қосындысының интегралы сол функциялар интегралдарының алгебралық қосындысына тең болады: . 3.Интеграл шектерінің орындарын ауыстырғанда интеграл таңбасы қарама-қарсыға өзгереді: .4. Интеграл шектері бірдей болғанда интеграл мәні нолге тең: . 5. Егер болса, онда m(b-a)< <M(b-a). 6.Егер с нүктесі [a;b] кесіндісінде жатқан нүкте болса, онда . 7. Орта мән туралы теорема. y=f(x) функциясы [a;b] кесіндісінде үзіліссіз функция болса, онда қандай да бір с [a;b] нүкте табылады да мына теңдік орындалады: (b-a)f(c). 8.Егер y=f(x) функциясы жұп болса, онда

2 . 9.Егер y=f(x) функциясы тақ болса, онда 0. 10. Ньютон-Лейбниц формуласы. F(b) – F(a), мұндағы . 11.Анықталған интегралдағы бөліктеп интегралдау: . 12.Анықталған интегралдағы айнымалыны алмастыру: .

f(x) және F(x) функциялары ақырлы немесе ақырсыз Х аралықта анықталған функциялар болсын.Х аралығында дифференциалданатын функциясы теңдігін қанағаттандырса, функциясы f(х) функциясының алғашқы функциясы деп аталады. Егер Х аралығында және Ф(х) функциялары f(х) функ-ның алғашқы функциясы болса, онда қандай да бір С саны табылып, мына теңдік орындалады: Ф(х)= F(x)+C .Бұл теоремадан егер функциясы f(х) функ-ның алғашқы функциясы болса, онда F(x)+C өрнегі f(х) функциясының барлық алғашқы функцияларының жиынын береді. f(х) функциясының алғашқы функ-ның жиыны f(х) функциясының анықталмаған интегралы деп аталады және деп белгіленеді, мұндағы - интеграл белгісі; f(х) – интеграл астындағы функция; f(х)dx - интеграл астындағы өрнек. Сонымен = F(x)+C , мұндағы F(x) – алғашқы функция, C –ерікті тұрақты

Қасиеттер: 1. . 2. . 3. = F(x)+C. 4. Берілген аралықта f(x) және g(x) функцияларының алғашқы функциялары бар болса, онда f(x)+g(x) функциясының да алғашқы функциясы бар болады және .

1	= C	2	= x+C
3	= +C, x>0,	4	= n|x|+C, x 0
5	= +C,	6	= +C
7	=sinx+C	8	=-cosx+C
9	=tgx+C,	10	=-ctgx+C,
11	=arcsinx+C, -1<x<1	12	=arcsin +C, -a<x<a
13	=arctgx+C	14	= artg +C
15	= ln +C	16	ln +C

5. . 6. Егер = F(x)+C болса, онда = F(ax+b)+C. 7. Егер интеграл астындағы функцияның алымы бөлімнің туындысы болса, онда интеграл бөлімнің абсолют шамасының наткрал логарифміне тең, яғни , мұндағы u=u(x).

№33. Айнымалыны алмастыру ж\е бөліктеп интегралдау әдісі. Айнымалыны алмастыру әдісі. I= интегралын қарастырайық. Айталық, x=g(t) дифференциалданатын функция болсын. Сонда dx=g’(t)dt және .Бұл әдіс айнымалыны ұтымды алмастыруға негізделген. Айнымалыны алмастыру арқылы интегралды бірден немесе бірнеше амалдардан кейін кестелік интегралға келтіріледі. Бөліктеп интегралдау әдісі. Бұл әдіс мынадай қатынасқа негізделген: d(uv) = udv + vdu udv = d(uv) – vdu мұндағы u=f(x) және v=g(x) функциялары туындылары бар функциялар. Теңдіктің екі жағынан да интеграл алсақ, , осыдан .Бұл әдісті қолданғанда u және v функцияларын интеграл интегралға қарағанда оңай алынатындай етіп таңдайды. Мысал: +С= +C.

№34. Қарапайым рационал өрнектерді интегралдау. түріндегі өрнекті n–дәрежелі көпмүшелік деп атайды. Мұндағы - нақты сандар ( , n>0). Көпмүшеліктердің қатынасы түрінде берілген өрнек рационал өрнек болады. Мысалы , бөлшектер рационал өрнектер. Егер бөлшектің алымындағы көпмүшеліктің дәрежесі бөліміндегі көпмүшелік дәрежесінен кем болса, бөлшек дұрыс деп, ал кем болмаса бөлшек бұрыс деп аталады. Мысалдағы біріншісі бөлшек - дұрыс, ал екіншісі – бұрыс бөлшек. Кез келген бұрыс бөлшекті алымын бөлімге бөлу арқылы дұрыс бөлшекке келтіріп алуға болады. Егер дұрыс рационал бөлшек бөлімі және түріндегі көбейткіштерге жіктелген болса, онда бөлшектімынадай қарапайым бөлшектердің қосындысына жіктеуге болады: , мұндағы, Р(х) – белгілі көпмүшелік, - белгісіз коэффициенттер. Ол коэффициенттерді табу үшін белгісіз коэффициенттер әдісін пайдаланамыз: теңдіктің оң жағын ортақ бөлімге келтіреміз; екі бөлшектің бөлімдері тең болатындықтан, алымдарын теңестіреміз; теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз; осы жүйені шешіп белгісіз коэффициенттерді табамыз. Мысалы бөлшегін қарапайым бөлшектер қосындысына жіктейік.

Бөлшек дұрыс, сондықтан бөлшекті жіктейміз, Белгісіз коэффициенттерді табу үшін теңдіктің оң жағын ортақ бөлімге келтіріп жазайық Бөлімдері бірдей, алымдарын теңестіреміз (оң жақтағы бөлшек алымын ықшамдап, х-тің дәрежесі түрінде жазайық: Теңдіктің екі жағындағы х айнымалының бірдей дәрежелері алдындағы коэффициенттерін теңестіру арқылы теңдеулер жүйесін аламыз:

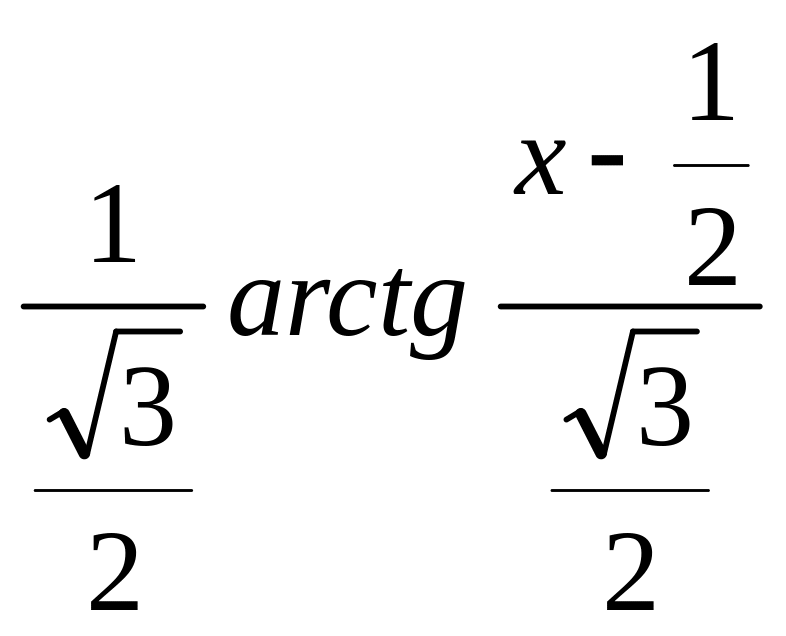Төрт белгісізді, төрт теңдеуден тұрған жүйені шешіп, белгісіз коэффициенттерді табамыз: .Табылған мәндерді теңдіктегі орнына қойып, бөлшектің қарапайым жіктелуін аламыз: .Енді осы рационал бөлшекті интегралдайық. Әр интегралды жеке қарастырайық. 1) , мұнда бөлшектің алымы бөлімінің туындысы болғандықтан 7-қасиетті пайдаландық.2) +С= +C= +C; 3) +4 +С= + +C, мұнда бірінші қосылғышты алымы бөлімінің туындысы болғандай етіп түрлендірдік те 7-қасиетті пайдаландық. Ал екінші қосылғышта бөлімінің толық квадратын бөліп алып, интегралдар кестесіндегі 14-формуланы пайдаландық.Сонымен ln|x+1|- + +C.

35. Ньютон-Лейбниц формуласы. Меншіксіз интеграл.

Ньютон-Лейбниц формуласы.

F(b) – F(a), мұндағы

37.Көп айнымалыдан тәуелді функция. Анықталу олысы. Деңгейлік сызықтар. Өмірде қандай да бір құбылыстар, оның ішінде экономикалық қатынастар да, бір неше шамалардың байланысы арқылы сипатталады. Осы байланыстарды зерттеу көп айнымалы функция ұғымын енгізуді қажет етеді. Анықтама. Қандай да бір Х жиынының элементтеріне қандай да бір заң немесе ереже бойынша z шама сәйкес қойылса, Х жиынында п айнымалыдан тәуелді функция берілген дейміз де z= деп жазамыз. Мұндағы айнымалылар тәуелсіз айнымалы немесе аргумент, ал z тәуелді айнымалы немесе функция, f – заң немесе ереже, ал Х - функцияның анықталу облысы болады.

Бұдан былайғы жағдайда екі айнымалыдан тәуелді функция қарастырамыз. Екі айнымалыдан тәуелді функцияға қатысты айтылған тұжырымдардың барлығын одан да жоғарғы айнымалыдан тәуелді функциялар үшін дұрыс болады. Екі айнымалыдан тәуелді функцияны z= деп белгілейміз. Бұл функцияның анықталу облысы хОу жазықтығында анықталады. Екі айнымалыдан тәуелді функция графигі үш өлшемді кеңістіктегі (х, у, z) нүктелердің геометриялық орнымен анықталатын қандай да бір бет болады. Мұнда х – абсцисса, у – ордината, z – апликата, және олар арасында z = f(x, y) функциялық байланыс бар z = С жазықтығымен қиғанда пайда болатын сызық z= f(x, y) функциясының деңгейлік сызығы деп аталады: f(x, y) = С Көп жағдайда функция графигін қарастырғаннан гөрі оның деңгейлік сызығын зерттеу оңай болады. z= f(x, y) функциясына бір айнымалыдан тәуелді екі функция сәйкес қоюға болады: х аргументті тұрақты деп (x=x₀) қарастырғанда z= f(x₀ , y) функциясын және у аргументті тұрақты деп (у=у₀) қарастырғанда z= f(x , y₀ ) функциясын.

№38. Дербес туындылар. Толық дифференциал. Z= f(x, y) функциясының дербес өсімшелерінің сәйкес аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған жағдайдағы шегі функцияның дербес туындысы дейді, былай жазылады:

Бұл анықтамадан z туындыны табу үшін у айнымалыны тұрақты деп, ал z туындыны табу үшін х айнымалыны тұрақты деп қарастыру керек. Және де бір айнымалы функция дифференциалынан белгілі дифференциалдаудың барлық ережелері сақталады. z= f(x, y) функцияның толық дифференциалы деп осы функцияның дербес туындыларының сәйкес аргумент өсімшелеріне көбейтіндісінің қосындысын айт: Егер f(x,y) = x, g(x,y) = y функциялары үшін қатынас бойынша толық дифференциалдарын тапсақ, df = dx= x, dg = dy= y болатындығы шығады. Олай болса функцияның толық дифференциалын мына түрде жазуға болады: .

39. Бағыт бойынша туынды және градиент. z= f(x, y) функциясы М(х,у) нүктесінің қандай да бір маңайында анықталған болсын және вектор бағытымен анықталатын қандай да бір l бағыт берілсін. Мұнда және бұрыштар векторының Ох және Оу осімен жасайтын бұрышы, ал - вектордың бағыттаушы косинустары деп аталады және

, . М(х,у) нүктесі l бағыт бойымен қозғалып М₁(х+ х, у+ у) нүктеге өзгергенде z функция z = f(х+ х, у+ у) - f(x, y)

өсімше алады. Егер ММ₁ = l болса, онда х= lcos , y= lcos , олай болса

=f(х+ lcos , у+ lcos ) - f(x, y).А

l

нықтама. z= f(x, y) функциясының l бағыт бойымен алған өсімшесінің l шамаға қатынасының осы шама нолге ұмтылғандағы шегі функцияның бағыт бойынша туындысы деп аталады, яғни

.Функцияның бағыт бойынша туындысының абсолют шамасы функция өзгеруінің жылдамдығын анықтайды, ал таңбасы функция өзгерісін («+» - өсетінін, «-» - кемитінін) сипаттайды. z= f(x, y) функциясының және дербес туындылары функцияның Ох және Оу остеріне параллель бағыт бойынша алынған туындылары болады. Бағыт бойынша туынды анықтамасынан

cos + cos болатындығы шығады. Егер l бағыт координаталарымен берілсе, яғни , онда бұл вектордың бағыттаушы косинустары былайша табылады:

cos = , cos =

Анықтама. z= f(x, y) функциясының градиенті деп координаталары ( , ) болатын векторды айтады және grad z деп белгілейді,

grad z= ( , )

формуланың оң жағында grad z= ( , ) векторы мен векторының скаляр көбейтіндісі тұр, олай болса бағыт бойынша туынды дегеніміз градиент пен бағытты анықтайтын бірлік вектордың скаляр көбейтіндісіне тең екен: ( grad z, ) Екі вектор бірдей бағытталғанда олардың скаляр көбейтіндісі ең үлкен мән қабылдайды. Олай болса grad z функцияның нүктедегі максималды жылдамдық (өсу) бағытын көрсетеді екен. Мынадай тұжырым дұрыс болады: Қандай да бір М(х₀,у₀) нүктеде дифференциалданатын z= f(x, y) функциясының градиенті сол нүкте арқылы өтетін деңгейлік сызыққа перпендикуляр болады.

№40. Екі айнымалы функцияның экстремумы. Қажетті ж\е жеткілікті шарттар. М(х₀,у₀) нүктенің жақын маңайында жатқан барлық (х, у) нүктелер үшін f(х₀,у₀) f(x,y) теңсіздігі орындалса, М(х₀,у₀) функцияның максимум нүктесі деп, ал f(х₀,у₀) f(x,y) теңсіздігі орындалса, М(х₀,у₀) функцияның минимум нүктесі деп аталады.Функция максимумы мен минимумы функция экстремумы деп аталады.Экстремумның қажетті шарты. М(х₀,у₀) нүктесі z= f(x, y) функциясының экстремум нүктесі болса, онда бұл нүктедегі функцияның дербес туындылары нолге тең, , . Экстремумның жеткілікті шарты. z= f(x, y) функциясы: 1) дербес туындылары нолге тең болатын , , М(х₀,у₀) нүктесінің маңайында анықталған болсын; 2) функцияның осы нүктеде екінші ретті үзіліссіз туындылары бар, , , . Онда, егер болса М(х₀,у₀) нүктеде экстремум бар, және егер A<0 – максимум, A>0 – минимум; ал болса М(х₀,у₀) нүктеде экстремум жоқ; болса М(х₀,у₀) нүктеде экстремумның бар жоқтығы белгісіз.

41. Дифференциалдық теңдеулер. Коши есебі.

ДИФФЕРЕНЦИАЛДЫ ТЕҢДЕУЛЕР Анықтама. Дифференциалды теңдеу деп х тәуелсіз айнымалы, у(х) ізделінді функция және оның түрлі ретті туындыларын өз ара байланыстыратын теңдеуді айтамыз .Дифференциалды теңдеу ретi деп теңдеудегі туындының жоғары ретін айтамыз. Мысалы, xy'+y=0, - бірінші ретті дифференциалды теңдеулер; - екінші ретті дифференциалды теңдеу; - үшінші ретті дифференциалды теңдеу. Бірінші ретті дифференциалды теңдеуді қарастырайық, . Егер осы теңдеу функция туындысына қатысты шешіліп тұрса, деп жазылады. Дифференциалды теңдеудегі орнына қойғанда оны тепе-теңдікке айналдыратын, дифференциалданатын y=q(x,С) функциясын теңдеудің жалпы шешімі деп айтамыз. . теңдеудің берілген бастапқы у(х₀)=у₀ шартты қанағаттандыратын шешімін табуды Коши есебі дейді. Дифференциалды теңдеудің шешімін табу процесін теңдеуді интегралдау дейді.

. 42 Айнымалыларды ажыратылатын дифференциалдық теңдеулер.Мысалдар. Айнымалысы ажыратылатын дифференциалды теңдеу. Егер теңдеу мына түрде: жазылатын болса, ол айнымалысы ажыратылатын дифференциалды теңдеу деп аталады. Бұл теңдеуді шешу үшін теңдеудің екі жағын көбейткішке бөлеміз: Сонда dx алдында тек х-тен тәуелді, ал dy алдында тек у-тен тәуелді функция тұрады да, теңдеудің айнымалылары ажыратылады. Енді теңдеуді мүшелеп интегралдап шешімін табуға болады: .Мысалы, xy'+y=0 дифференциалды теңдеудің шешімін табайық. екенін ескеріп теңдеуді мына түрде жазайық: . Теңдеудің екі жағын ху көбейткішке бөліп айнымалысын ажыратамыз: . Мүшелеп интегралдасақ, lny+lnx=lnC, осыдан екендігі шығады.

№43. Бірінші ретті біртекті сызықты дифференциалдық теңдеулер.Мысалдар. Бiрiншi реттi дифференциалды теңдеу сызықты деп аталады, егер ол мынадай түрде жазылатын болса: y'+P(x)y=Q(x) Егер (5) теңдеудегі Q(x)=0 болса сызықты теңдеу біртекті деп аталады. y'+P(x)y=0 Сызықты біртекті дифференциалды теңдеу шешімін айнымалыны алмастыру әдісімен бірден алуға болады: Мысал. дифференциалды теңдеуді шешу керек.Шешуі. Теңдеудің екі жағын х-ке бөлсек, сызықты теңдеу аламыз: , мұнда P(x)= , Q(x)=2x³ . Теңдеудің шешімін табу үшін формула қолданамыз. Сонымен, берілген сызықты теңдеу шешімі: .

№46.Ықтималдықтың классикалық ж\е статистикалық анықтамасы. Тәжірибедегі ізделінді оқиғаның пайда болуына қолайлы жағдайлар санының, барлық элементар оқиғалар санына қатынасы оқиға ықтималдығы деп аталады және Р әрпімен белгілейді:

мұндағы А – ізделінді оқиға, т - осы оқиғаның пайда болуына қолайлы жағдайлар саны, п - элементар оқиғалар саны. Осы анықтаманы ықтималдықтың классикалық анықтамасы деп атайды.

Статистикалық тұрақтылық пайда болған кездегі салыстырмалы жиілік оқиға ықтималдығы деп қабылданады . Бұл анықтаманы ықтималдықтың статистикалық анықтамасы деп атайды.