
- •Обчислювальний експеримент. Теорія попиту.
- •Абсолютна і відносна похибки
- •Методи розв’язання системи лінійних рівнянь (слр). Прямі методи слр.
- •Метод Гауса чисельного розв’язку слр.
- •Вивід розрахункових формул
- •Модифікація методу Гауса
- •Умови застосування методу Гауса і його зв'язок з розкладом матриці на множники.
- •Обчислення визначника
- •Обчислення обернених матриць
- •Обумовленість с-ми лінійних рівнянь Стійкість слар
- •Обумовленість слар, число обумовленості
- •Метод прогонки для розв’язання слар
- •Ітераційні методи розв’язання слар
- •Ітераційний метод Якобі
- •Ітераційний метод Зейделя
- •Канонічна форма однокрокових ітераційних методів
- •Приклад розв’язання методом Зейделя та Якобі
- •Метод простої ітерації
- •Дослідження збіжності ітераційних методів
- •Необхідна і достатня умова збіжності у стаціонарних методах
- •Оцінки швидкості збіжності стаціонарних ітераційних методів
- •Многочлени Чебишева 1-го роду і многочлени Чебишева на відрізку [0,1]
- •Многочлен Чебишева на проміжку [a,b]
- •Ітераційні методи Чебишовським набором параметрів
- •Неявний Чебишевський ітераційний метод
- •Інтерполяція функцій
- •Інтерполяційний многочлен Лагранжа
- •Розділені різниці. Інтерполяційний многочлен Ньютона
- •Властивості розділених різниць
- •Побудова інтерполяційного многочлена Ньютона
- •Приклад
- •Скінченні різниці
- •Формула залишкового члена інтерполяційного многочлена Лагранжа
- •Інтерполяції за допомогою раціональних функцій
- •Інтерполювання періодичних функцій
- •Інтерполяційний многочлен Ерміта
- •Збіжність інтерполяційних процесів
- •Інтерполяція сплайнами
Формула залишкового члена інтерполяційного многочлена Лагранжа
У
випадку коли
заміняємо на
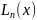 .
.
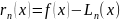 ̶ похибка
інтерполювання
̶ похибка
інтерполювання
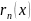 ̶ залишковий член інтерполяційного
многочлена
̶ залишковий член інтерполяційного
многочлена
Оцінимо
дану похибку в

Для цього ми введемо в розгляд функцію:
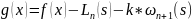 (1)
(1)
Де k-const
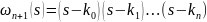 (2)
(2)
Необхідно
оцінити
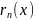 в
в
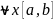 ,
,
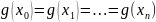 ̶ який не э вузлом інтерполяції
̶ який не э вузлом інтерполяції
k
в
(1) будемо
шукати з припущення, що
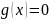 для тієї точки, для якої проводимо
оцінку.
для тієї точки, для якої проводимо
оцінку.
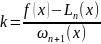 ;
;
має
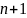 Неперервну похідну на проміжку [a,b],
а функція
Неперервну похідну на проміжку [a,b],
а функція
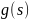 має менше ніж
має менше ніж
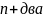 нули
на [a,b].
нули
на [a,b].
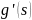 має не менше
ніж
”0” на [a,b].
має не менше
ніж
”0” на [a,b].
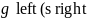 має не менше
ніж
має не менше
ніж
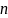 нулів.
нулів.
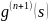 має хоча б
1 нуль.
має хоча б
1 нуль.
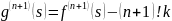
Ǝ
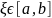
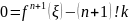
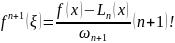
тоді похибку інтерполяції можемо представити у вигляді:
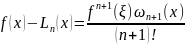 (3)
(3)
З (3) можемо зробити висновок, що інтерполяційний многочлен Ньютона є точним для многочлена степеня n.
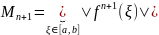
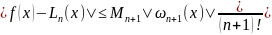 (4)
(4)
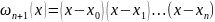
Мінімізація похибки інтерполяційного многочлена в конкретних випадках ми можемо оцінити верхню межу n+1 похідної.
Величина похибки (4) буде залежати від величини.
Max|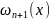 |
̶ мінімізація такої величини
відбувається за допомогою вибору вузлів.
|
̶ мінімізація такої величини
відбувається за допомогою вибору вузлів.
Ця задача розв’язуеться за допомогою многочлена Чебешева 1-го роду.
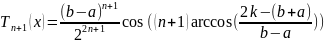 (5)
(5)
Тоді за вузли інтерполяції доцільно вибрати корені многочлена виду (5),
 ,
,
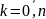 (6)
(6)
Тоді
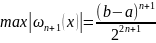 ,
,
Тоді
(4):
 (7)
(7)
Інтерполяції за допомогою раціональних функцій
Деколи нам зручніше будувати наближену функцію за допомогою раціональних або дробово-раціональних функцій.
Нехай
функція
задана своїми значеннями у вузлах
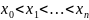 і потрібно побудувати функцію:
і потрібно побудувати функцію:
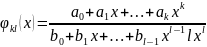 (1)
(1)
Де
числа
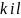 є додатніми і виконується:
є додатніми і виконується:
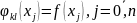 (2)
(2)
І повинна виконуватись умова близькості (2).
Рівність
(2) представляє собою СЛАР з
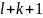 змінними
змінними
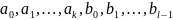 .
.
Будемо
вимагати, щоб кількість рівнянь системи
співпадала з кількістю невідомих, тобто,
щоб
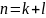 ;
;
Тоді отримаємо систему рівнянь:
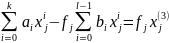 (3)
(3)
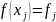 ,
,
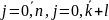
Із
системи (3) нам потрібно знайти коефіцієнти
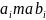 ,
де
,
де
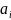
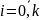 ,a
,a
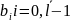 .
.
Система (3) э достатньо громосткою, тому досить часто використовують дробово-лінійні інтерполяції, де інтерполяційний многочлен знаходиться за формулою:
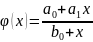 ,
,
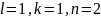 (4)
(4)
Припустимо, що функція задана у трьох вузлах інтерполяції:
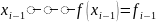
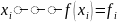
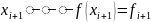
Виконується
умова близькості
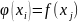 :
:
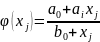 ;
; 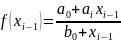 ;
;
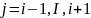 ;
;
Ця
задача є частиггим випадком системи
(3) при
 ,
то для визначення коефіцієнта
,
то для визначення коефіцієнта
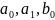 побудуємо систему виду (3).
побудуємо систему виду (3).
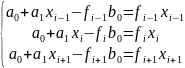
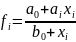 ;
; 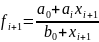 ;
;
Знайдемо розв’язок даної системи у явному вигляді:
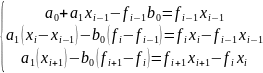
Введемо у розгляд позначення:
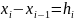 ;
; 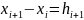 ;
;
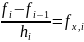 ;
; 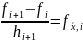 ;
;
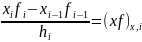 ;
; 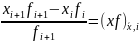 ;
;
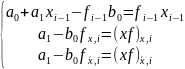
Якщо
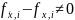 ,
то з останнього рівняння можемо знайти
.
,
то з останнього рівняння можемо знайти
.
Знайшовши , підставимо у рівність (4).
Зауваження. Будуючи інтерполяційний многочлен за допомогою раціональних функцій необхідно слідкувати, щоб знаменник виразу (1) або (4) не перетворився в 0.
Іншим
моментом є вибір таких вузлів інтерполяції,
при якому чисельник виразу (1) ділиться
без остачі на знаменник. У цьому випадку
дробово-лінійна функція
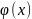 перетвориться у константу.
перетвориться у константу.
Ці випадки можуть бути виключеними при розв’язуванні системи (3).
Інтерполювання періодичних функцій
Нехай
нам необхідно деяку функцію
,
яка визначена на проміжку
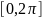 і є періодичною на цьому проміжку з
періодами. Побудуємо деяку інтерполяційну
функцію, яка у вузлах інтерполяцій на
проміжку
набуває тих самих значень, що і функція
.
і є періодичною на цьому проміжку з
періодами. Побудуємо деяку інтерполяційну
функцію, яка у вузлах інтерполяцій на
проміжку
набуває тих самих значень, що і функція
.
Так, як функція є періодичною функцією, то інтерполяційний многочлен будемо шукати у вигляді тригонометричного многочлена.
За
систему функцій
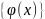 виберемо систему тригонометричних
функцій, які періодичними на проміжку
і
виберемо систему тригонометричних
функцій, які періодичними на проміжку
і
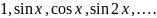
Можна показати, що на проміжку система функцій:
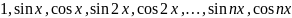
при
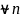 є системою функцій Чебешева, тобто ⍱
тригонометричного многочлена вигляду
є системою функцій Чебешева, тобто ⍱
тригонометричного многочлена вигляду

на
проміжку
має, більше ніж
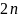 додатніх коренів. Тому для кожної
визначеної на проміжку
періодичної функції з періодом
додатніх коренів. Тому для кожної
визначеної на проміжку
періодичної функції з періодом
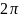 при ⍱
наборі
при ⍱
наборі
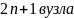 і
і
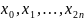 із
проміжку
із
проміжку
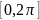
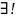 тригоносетричний
многочлен
для функції
,
який на заданій системі вузлі, для якого
викон
тригоносетричний
многочлен
для функції
,
який на заданій системі вузлі, для якого
викон
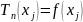 ,
,
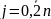 і такий многочлен має наступний вигляд:
і такий многочлен має наступний вигляд:
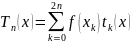 , де
, де
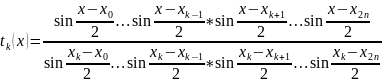
Тому
для такого вибору
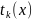 , буде виконуватись умова близькості
,
.
, буде виконуватись умова близькості
,
.
