7.Теорема Лагранжа и ее применения к исследованию функции.

Т. Ролля. Пусть функция f определена на отрезке [а;b] и удовлетворяет трем условиям:

1. функция непрерывна на этом отрезке;

2. функция дифференцирована в интервале (а,b);

3. функция на концах отрезка имеет одинаковые значения f(а)=f(b). Тогда существует т. с на отрезке [а,b] со св-вом f(с)=0. Теорема Лагранжа. Если функция f задана на [а;b] и удовлетворяет усл. 1 и 2 теоремы Ролля. Тогда существует т. с на (а,b): f(b)-f(a)=f'(с)(b-a).

Док-во: Составим вспомогательную функцию φ(x)=r*x+f(x), где r – постоянная. Эта функция непрерывна на [а;b] как разность непрерывных функций и дифференцируема на (а;b). Подберем коэффициент r так, чтобы выполнялось равенство φ(a)=φ(b), то есть r*a+f(a)=r*b+f(b). Это r=(f(a)-f(b))/(b-a). При таком r функция φ удовлетворяет условиям 1-3 теоремы Ролля. Отсюда по Т.Ролля существует с из (а;b):φ'(с)=0. Вычислим φ’(x): φ’(c)=(r*x+f(x))’|_x₌_c=r+f’(c). Т.о. r+f’(c)=0, а тогда , что равносильно f’(c)= -r доказываемой формуле.

Геометрический смысл Т.Лагранжа:

заметим, что формула Лагранжа равносильна равенству f’(c)=(f(b)-f(a))/(b-a), первая часть которого численно равна

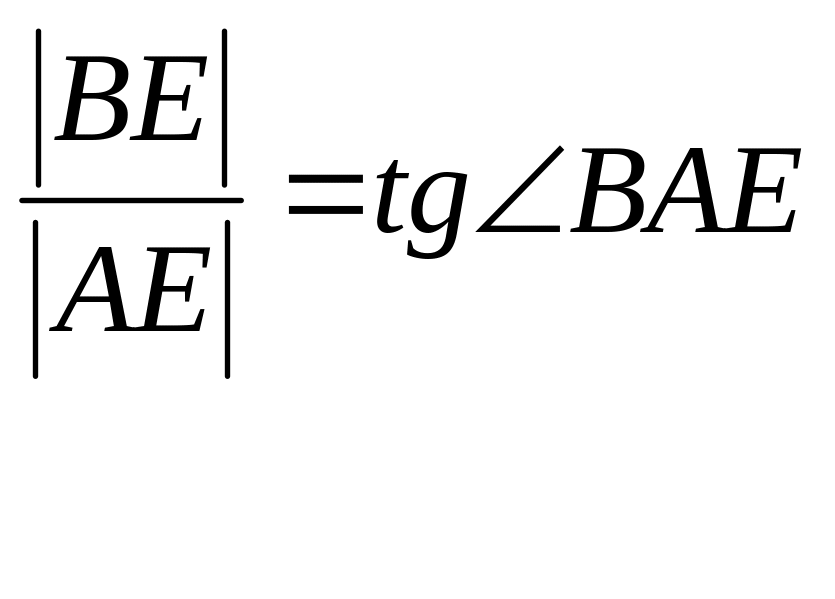
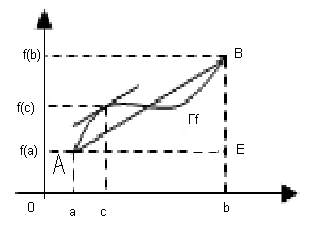
Учитывая геометрический смысл f’(c) выводим, что в условиях Т. Лагранжа на графике функции f найдется точка с координатами (c;f(с)), касательная в которой к графику параллельна хорде [AB]. Т.о. Формула Л. означает, что на кривой АВ существует М, в которой касательная параллельна секущей АВ.

Применение теоремы Лагранжа:

1. Критерий постоянства функции:

пусть функция f задана на [а;b] и выполнены условия 1 и 2 T. Ролля.

Для того, чтобы функция была постоянной на [а;b], необходимо и достаточно, чтобы f(х)=0 для любого х из (а,b).

Док-во: “=>” Для каждого фиксированного х из полуинтервала (a;b] на сегменте [a;x], очевидно, выполнены условия 1-2 Т. Ролля. Следовательно, по Т.Лагранжа на интервале (а;х) найдется точка с_х такая, что f(x)-f(a)=f’(c_x)*(x-a). Отсюда, ввиду f’(c_x)=0, получаем равенство f(x)-f(a)=0, т.е. f(x)=f(a). поскольку аргумент х был произвольным, существование постоянной с установлено. Док-во обратной импликации очевидно.

2. Критерий нестрогой монотонности.

Пусть f задана на [а;b], выполняется 1 и 2 Т. Ролля. Для того, чтобы функция была нестрого возрастающей (убывающей) на [а;b] необходимо и достаточно, чтобы производная f(х)>0(f(х)<0).

3. Достаточное условие строгой монотонности: Пусть функция f удовлетворяет условиям 1 и 2 Т. Ролля. Тогда, если f’(x)>0 для всех х из (a;b), то функция f строго возрастает на [а;b] (убывает).

Док-во: Пусть x₁,x₂€[a;b] и x₁<x₂. Т.к. [x₁;x₂]с[a;b], то функция f непрерывна на [x₁;x₂] и дифференцируема на (x₁;x₂). Следовательно, по Т. Лагранжа найдется точка с из (x₁;x₂), для которой f(x₂)-f(x₁)=f’(c)*(x₂-x₁). Отсюда, в силу неравенств x₂-x₁>0 и f’(c)>0 получаем неравенство f(x₂)-f(x₁)>0, что равносильно f(x₂)>f(x₁). Формулировка признаков убывания, а также невозрастания и неубывания аналогичны.

8.Точки mах и min функции. Необходимое условие экстремума. Достаточное условие экстремума.

Опр1. Пусть t– внутренняя точка D(f). Точка t наз-ся точкой max (min) если сущ-т такой интервал

Что

Точки max и min наз-ся т. экстремума.

Для поиска точке экстремума функции важно знать необходимые условия экстремума. Их предоставляет следующая теоерма.

Т. Ферма. Если t – точка экстремума функции f(x), и если сущ-т f’(t), то f’(t)=0.

Опр. 2. Точка х наз. критической или стационарной точкой функции f, если функция дифференцируема в т. t и при этом f’(t)=0.

Необход. Условие экстремума дает т-ма 1

Т.1. Если t- т. экстремума ф-и f(x), то:

1. f’(t) не сущ-т

2. t -критическая точка

Док-во: 1)Если выпол-ся св-во 1., то док-ть нечего, такие точки экст-ма дейс-но сущ-т, нап-р, для ф-и f

, точка min t=0, в которой производной нет.

2) Пусть f’(t) сущ-т, тогда по т. Ферма f’(t)=0 и поэтому t- крит. точ. ф-и. Ч.Т.Д.

Точка t – удов-т усл-м 1. наз-ся подозрит-й на экстремум. Отметим, что не всякая подоз-я на экстремум точка яв-ся на самом деле т. экс-ма.

В самом деле рассм-м ф-ю , сущ-т и обращ-ся в ноль, т.е. 3x²=0 след-но t=0,т.е. эта т-ка яв-ся подоз-й на экст-м. Однако, если смот-ть на график, то Дей-ой т. на экстремум она не яв-ся, на самом деле это точка перегиба. Поэтому условий неск-ко, мы докажем одно из них.