
- •1. Предел п-ти. Ариф-ие св-ва пределов.
- •3. Отображения мн-в (ф-ии). Предел ф-ии в точке. Арифметические св-ва пределов.
- •4. Непрерывность функции в точке. Свойства функций непрерывных на отрезке.
- •7.Теорема Лагранжа и ее применения к исследованию функции.
- •8.Точки mах и min функции. Необходимое условие экстремума. Достаточное условие экстремума.
4. Непрерывность функции в точке. Свойства функций непрерывных на отрезке.
О1. aЄD(f).Функция f с областью определения D(f) наз. непрерывной в точке a, если выпол-ся рав-во limf(x)=f(a) при x→a. Если это рав-во нарушено, то а-т.разрыва ф-и f. Ф-я f, непр-я в каждой т.мн-ва Е наз-ся непр-й на мн-ве Е.
Из ариф-х св-в предела фун-и в точке автоматически получ-ся след-я т-ма.
Т1. Если функции: f и g нпр в точке а, аЄD(f)∩D(g). то в этой точке нпр и функции f±g, f·g, а при g(a)≠0 и функция f/g.
О2. Функция f наз. непрерывной на мн-ве Е, если она непрерывна в каждой точке из мн-ва Е //заметим, что при этом необходимо выполнятся ЕcD(f)//.
Т2.(Больцано
– Коши)
Если
функция f
определена и нпр
на отрезке [а, b]
и на его концах принимает значения разных знаков
![]()
, тогда
![]()
Док-во:(Методом
деления отр.пополам) Разделим отрезок
(а, в) пополам точкой (а+в)/2. Случ-но м\т
оказ-ся, что в этой точке функция обратится
в 0, тогда обозначим
с=(а+в)/2 и доказательство закончено.
Поэтому будем
считать, что значение в этой точке f≠0.
Обозначим через
![]() ту половину, на концах кот. Знаки ф-и
различны. Для этого отрезка мы имеем:
f(a1)f(b1)<0.
и b1-a1=(b-a)/2
ту половину, на концах кот. Знаки ф-и
различны. Для этого отрезка мы имеем:
f(a1)f(b1)<0.
и b1-a1=(b-a)/2
На след. шаге разобьём пополам [а1,b1] Если в т. деления ф-я обращ-ся в 0, то обозначим ее буквой с и закончим док-во. Если это не так, обозначим через [а2, b2] ту половину [a1,b1], на концах которой функция принимает значения разных знаков f(a2)f(b2)<0. и b2-a2=(b-a)/22
Продолжим этот процесс послед-го деления отр-в пополам и выбора той из половин, на концах кот. Значения ф-и имеют различ. знаки.
Возможны 2 варианта:
1. В какой – то из точек ф-я обратиться в 0.
2. На n –ом шаге мы получим:
[an,bn]c[an-1,bn-1], f(an)f(bn)<0 (1) и bn-an=(b-a)/2n
……………………………
При этом мы будем иметь: [a,b]c[a1,b1]с[a2,b2]c…с[an,bn]c…, т.е отрезки вложены друг в друга.
lim(bn-an)=lim((b-a)/2n)=0
Отрезки
стяг-ся. Тогда по принципу Кантора
стяг-ся отрезков:
Ǝ!c=liman=limbn(2).
Т.к. совершенно ясно, что
![]() ф-я
f
б/т нпр в т. с
ф-я
f
б/т нпр в т. с
Тогда из соот-й (2) мы получим:
limf(an)=f(c)
limf(bn)=f(c)
Из (1): limf(an)f(bn)≤0
f2(c)≤0f(c)=0. чтд.
Как следствие из т-мы 1 получается т-ма 2 о промежуточном значении.
Т.3.
Пусть
f
нпр на отрезке [а,b]
и на
его концах принимает неодин-е значения
![]()
Тогда
какого бы ни было число С, лежащее между
А и В,
найдется такая точка
![]()
Док-во: Пусть для определенности А<В. Вспомогательная функция h(x)=f(x)-C, очевидно, непрерывна на [a,b]. Т.к., кроме того h(a)=f(a)-C=A-C<0, h(b)=f(b)-C=B-C>0, то по Т.2. существует с€(a,b) со св-вом h(c)=0, т.е. f(c)-C=0 или f(c)=C.
О3:Ф-я f, опр-я на мн-ве Е наз-ся огр-й сверху (снизу) на мн-ве Е, если ƎМ: f(x)≤M(f(x)≥M) для люб. xЄE. Ф-я f наз-ся огр-й, если она огр-на и сверху и снизу.
1 сп.
Сущ. m
и M:
![]()
2 сп.
Сущ. М:
![]()
Т.4.(1-я т-ма Вейер-са). Каждая непрерывная функция f на отрезке [а,b] ограничена на нем.
Теорема 5 (2-я т. Вейер-са). Если функция непрерывна на [а,b], то она принимает на нем свои наименьшее и наибольшее значение.
Крат.
Запись: f
нпр на [а,b].
Док-ть, что
![]()
![]()
Док-во: (Для наиб. Знач.)
Обозначим A= Suр Е (f). Этот Suр сущ-т т.к. по 1-й т-ме В-са мн-во значений ограниченно и по т-ме о гранях мы должны док-ть, что сущ. х0 из [a;b]:f(х0)=A. Д-во проведем от противного.
допустим,
![]()
Тогда введем вспомогательную функцию
g(x)=1/(A-
f(x)),
![]() .
Ф-я
g(х)
нпр как частное 2-х нпр, причем A-
f(x)≠0═>
по Т.4 ограничена на этом отрезке:
.
Ф-я
g(х)
нпр как частное 2-х нпр, причем A-
f(x)≠0═>
по Т.4 ограничена на этом отрезке:
![]()
![]()
Пос-ку
g(x)
полож. g(x)≤M
![]()
![]()
Последнее неравенство означает, что число
A- 1/M мажоранта Е(f),но это невозможно, пос-ку число А будучи Sир Е (f) яв-ся самой маленькой из мажорант. Это противоречие доказывает теорему.
5. Опр-ие производ. ф-ии в точке. Ариф-ие св-ва произв-й. Геометр-ий смысл производной.
О![]() 1.Пусть
ф-ия f(x)
опред.на неккот интервале, содерж-ий
т.t,
т.е. t
- внутренняя точка D(f)
Если существует конечный предел ,
1.Пусть
ф-ия f(x)
опред.на неккот интервале, содерж-ий
т.t,
т.е. t
- внутренняя точка D(f)
Если существует конечный предел ,
, то он наз-ся производной ф-ии f в точке t и обозначается через f’(t). Ф-ия f называется дифференцируемой в точке t. Если произв-ая Ǝ в кажд.точке мн-ва Е, то ф-ия наз-ся диффер-ой на Е.
Т\о f’в точке t (f’(t))-число.
Если же ф-ия диффер-ма на мн-ве Е, то сопоставляя каждому числу хЄЕ произв-ю f’(х) мы получаем производную ф-ию f’(х),определенную на Е.
Лемма. Если ф-ия f дифференцируема в точке t, то она и непрерывна в этой точке t.
Док-во: Т.к. при х≠t
![]() еханике
принято считать, что точки в момент
материальной точки на это материальная
точка движется прямолинейно по закону
еханике
принято считать, что точки в момент
материальной точки на это материальная
точка движется прямолинейно по закону
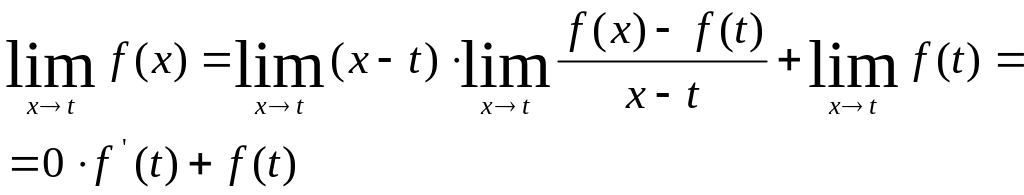
Геометрический смысл производной:
⊔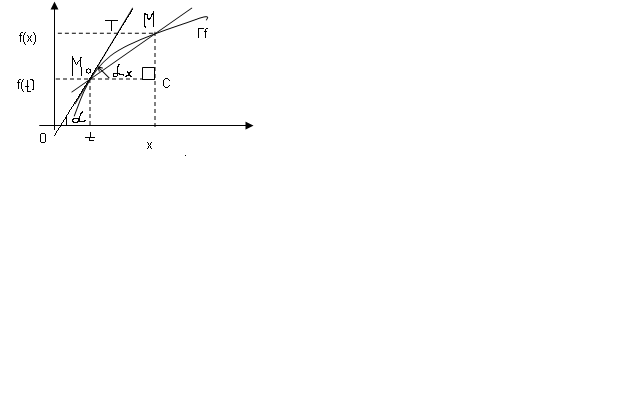 задана
некот.кривая и на ней т.М0.
Возьмем М и проведем секущую. Б\м двигать
т.М по направ. К т.М0
по кривой. Секущая М0М
поворачивается в т.М0.
задана
некот.кривая и на ней т.М0.
Возьмем М и проведем секущую. Б\м двигать
т.М по направ. К т.М0
по кривой. Секущая М0М
поворачивается в т.М0.
Если при стремлении т.М к т.М0 вдоль кривой секущая занимает предельное положение М0T, то МТ наз-ся касательной.
⊔ теперь задана ф-ия f(x), про ктр известно, что Ǝ f’(t). Возьмем х≠t. M0(t, f(t)), M(x, f(x)). Обе лежат на кривой y=f(x)
Проведем секущую М0М и ⊔ обозначен ч\з αх – угол наклона М0М к оси ОХ. Заметим, что МС=f(x)-f(t). M0C=x-t.
Из треуг-ка М0МС мы получ.что tgαx=МС/М0С=(f(x)-f(t))/(x-t), де х→t.
Тогда ясно:
М→М0 вдоль кривой у=f(x)
М0М поворачивается в точке М
αх меняется
По
условию дано. Что Ǝ
f’(t),
значит
Ǝ
f’(t)=
![]()
С![]() ущ-ие
предела
ущ-ие
предела
Означает, что сам угол αх→k
Предельному положению, а именно к углу α, определенному α═arctgk
По вышесказанному это значит, что гафик ф-ии имеет в т.М0 касательную, наклоненную к оси ОХ под углом α, а потому имеющую угловой коэф-т k=tgα=f’(t).
Получили след.геом-ий смысл произв.: производная ф-ии f в точке t равна тангенсу угла наклона касательной L к графику функции f в точке M0 с координатами (t, f(t)):
Т.1.
Пусть функции f
и g
дифференцируемы в точке t
и пусть t
– внутренняя точка мн-ва D(f)∩D(g).
Тогда в точке t
дифференцируемы ф-ии f+g,
f-g,
f*g,
а при g(t)≠0
и ф-ия f/g.
При этом выполняются следующие равенства: Док-ва во всех 4 случаях сходны. Остановимся
подробнее на примере ф-ии f*g.
Док-во: Чтобы док-ть существование
(f*g)’(t)
и вычислить ее заметим, что.
Док-ва во всех 4 случаях сходны. Остановимся
подробнее на примере ф-ии f*g.
Док-во: Чтобы док-ть существование
(f*g)’(t)
и вычислить ее заметим, что.
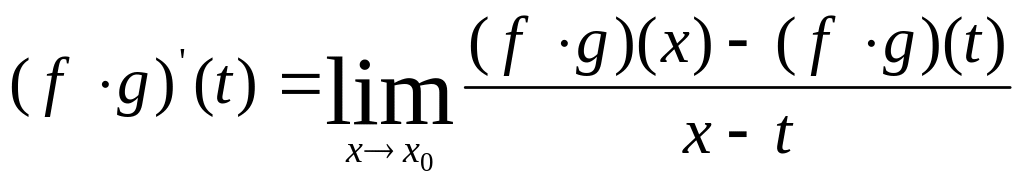 .
.
D(fg)=D(f)∩D(g)
X0-
внутренняя точка D(f)=>
δ1
– окрестность точки х0:![]()
t
– внутренняя точка D(g)=>
δ2
– окрестность точки t:![]()
Рассмотрим δ=min{δ1; δ2}
(t- δ;t+ δ)c(t-δ1;t+ δ)cD(f)|
(t- δ;t+ δ)c(t- δ;t+ δ)cD(g)| =>(t- δ;t+ δ)cD(f)∩D(g)
Представим выражение под знаком предела в удобной форме:
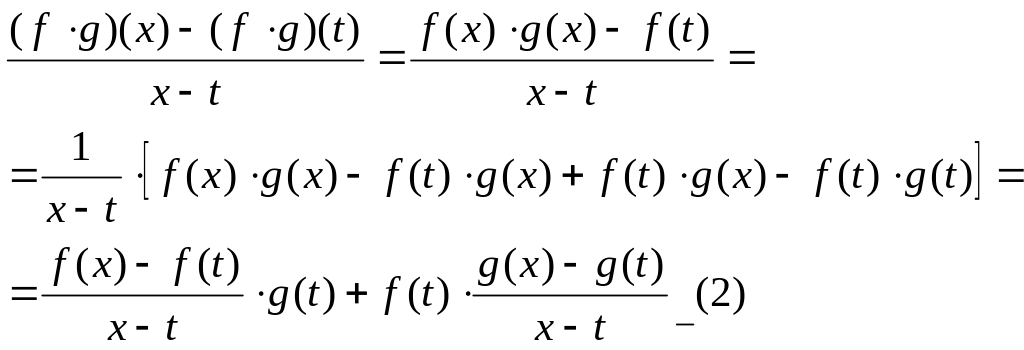 Т.к.
при х→t,
в силу лемме, g(x)→g(t),
а из дифференцируемости ф-ий f
и g
в точке t,
следует
Т.к.
при х→t,
в силу лемме, g(x)→g(t),
а из дифференцируемости ф-ий f
и g
в точке t,
следует![]() , то по Т.( Если существуют конечные
пределы ф-ий f
и g
в точке t,
причем t
– точка прикосновения мн-ва D(f)∩D(g),
то в ней существуют пределы функций
f+g,
f-g,
f*g)
существует предел выражения (2), причем
он равен именно правой части доказываемой
формулы 3.
, то по Т.( Если существуют конечные
пределы ф-ий f
и g
в точке t,
причем t
– точка прикосновения мн-ва D(f)∩D(g),
то в ней существуют пределы функций
f+g,
f-g,
f*g)
существует предел выражения (2), причем
он равен именно правой части доказываемой
формулы 3.
//Для док-ва 4.:![]()
По условию
![]() по Лемме: y=g(x)
непрерывна в точке t
т.е.
по Лемме: y=g(x)
непрерывна в точке t
т.е.![]()
Рассмотрим
g(t)>0=>![]() по
Т. о локальном сохранении знака(если
предел в точке >0, то существует
окрестность этой точки, во всех точках
которой знак тоже положительный)=>
по
Т. о локальном сохранении знака(если
предел в точке >0, то существует
окрестность этой точки, во всех точках
которой знак тоже положительный)=>
![]() δ=min{δ1,δ2,δ3}
δ=min{δ1,δ2,δ3}
(t-δ;t+δ)c(D(f)∩D(g))\{x:g(x)=0}//
Т.2. Пусть функция f дифференцирована в т.x0, причем f(x0)≠0. Пусть Т=f(x0) и на некотором интервале, содержащем Т определена обратная функция F(х), непрерывная в т. Т. Тогда эта функция дифференцирована в т. Т, причем F'(Т)=1/f(x0).
Т.3. Пусть функция f дифференцирована в т. x0 и пусть в некотором интервале, содержащем т. x0 определена следующая функция
S(x)=g◦f(x)=g(f(х)). Обозначим Т=f(x0). Если внешняя функция g дифференцирована в т.Т, то сложная функция S(х) дифференцирована в т. x0, причем S’(x0)=g’(T)*f ’(x0)=
=g’(f(x0))*f ’(x0), т.е. производная композиции равна произведению производных, составляющих эту функцию.
 6.
Диф-сть ф-и и ее диф-л.Геом-кий смысл
диф-ла ф-и в точке.
6.
Диф-сть ф-и и ее диф-л.Геом-кий смысл
диф-ла ф-и в точке.
y=f(x).
t
– внутренняя точка ее обл.опр. Если
взять х≠t,
хЄD(f),
то мы обозн.ᇫx=x-t
и б\м наз-ть приращением аргумента, а
ᇫy=f(x)-f(t)
б\м наз-ть приращением ф-и. Заметим, если
Ǝ
![]()
О1. Если Ǝ такая постоянная А=const, что вып-ся ᇫy=Aᇫx+αᇫx (1), где α→0 приᇫx→0, то говорят, что ф-я y=f(x), диф-ма в т.t.
Само же выр-е Аᇫx наз-ся диф-лом ф-и в т.t и обозн.dy или df(t).
Мы выясним связь м\у диффер-тью ф-и в т.t и сущ-ем произв-й ф-и в этой т.
Теорема 1. Для того, чтобы ф-я y=f(x) была диф-ма в т.t необх-мо и дост-но, чтобы в этой т. Ǝ произв-я y’=f’(t), причем при вып-ии этого условия рав-во (1) имеет место титтк А= y’=f’(t)
Док-во: 1.Необх-ть.
⊔ ф-я диф-ма в т.t,
то есть вып-но рав-во (1). Считая, чтоᇫx≠0
разделим обе части рав-а (1) наᇫx:
ᇫy/ᇫx=А+α.
Устремимᇫx→0,
тогда
![]()
f’(t)=А+0=>A=f’(t)
2.Дост-ть.
⊔![]() Ǝ
f’(t),
тогда
Ǝ
f’(t),
тогда
Поскольку разность м\у ф-ей и ее пределом яв-ся беск-но малой мы м\м написать ᇫy/ᇫx=f’(t)+α, где α→0 приᇫx→0.
Умн-м части последнего рав-ва на ᇫx≠0: ᇫy=f’(t) ᇫx+αᇫx.
Мы получили рав-во (1), в ктр.А=f’(t). Читд.
ОЗ. Дифференциалом независимой переменной наз. произвольное приращение независимой переменной (аргумента) d(х)= Δх.
О4. Дифференциалом функции f(х) наз. произведение ее производной на дифференциал аргумента dу = df(x)=f ‘(х)d(х). Дифференциал аргумента совпадает с приращением аргумента, а дифференциал функции в общем случае не совпадает с ее приращением.
Пример: y=x => y’=1 => dy=1*∆x=∆x
Геом.смысл дифференциала функции. Функция предполагается дифференцированной в т. х0 d(x)=Δх=МС Δf(x)=AC f ‘(x)=tg∟BMC
Но df(x)=f(x)∆х=MC*tg∟BMC=BC
Д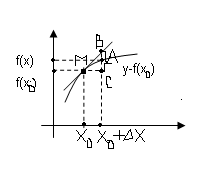 ифференциал
функции изображается BC≠AC,
изображающий приращение функции, т.е.
если ∆f(x)
– приращение ординаты кривой y=f(x),
то df(x)
– это приращение ординаты касательной
к кривой в точке A.
Это и есть геометрический смысл
дифференциала.
ифференциал
функции изображается BC≠AC,
изображающий приращение функции, т.е.
если ∆f(x)
– приращение ординаты кривой y=f(x),
то df(x)
– это приращение ординаты касательной
к кривой в точке A.
Это и есть геометрический смысл
дифференциала.
Т.к.dy=y’dx, то умножая функции таблицы производных на dx мы получим таблицы дифференциалов.
Т.2. Если функции f и g дифференцированы в точке x0, то в этой точке дифференцированы функции f±g,f·g,f/g при g(x0)≠0, c·f при c –const, причем выполняются равенства:
1.d(f±g)=df±dg;
2. d(f·g)=gdf+fdg;
3. d(f/g)=(gdf-fdg)/g2;
4. d(cf)=cdf, при c-const.
Док-во(3): f дифференцирована в точке х0 => существует f’(x0)
g дифференцирована в точке х0 => существует g’(x0), т.о.существует (f/g)’(x0), g(x0)≠0 (f/g)’=(f’g-fg’)/g2
Теперь xdx
![]()
(остальные аналогично).
