24. Предел последовательности. Арифметические св-ва пределов.

Опр.1. Числовой послед-тью наз-ся всякое отображение f: N→R при этом для краткости записывают а_n=f(n) и наз-т n-м членом послед-ти, а сама посл-ть изображ-ся (а_n).

Опр.2. Число а€R наз. пределом числовой послед-ти (a_n), если для каждого положительного действительного числа ε найдется натуральное число n, такое, что как только n≥n₀ так сразу Іa_n-aІ<ε.

Символическая запись опр.:

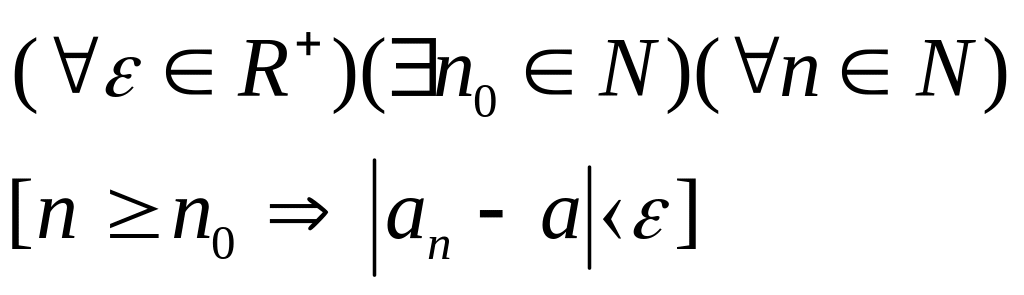
Послед-ть (a_n), имеющая пределом число а, наз. Сходящейся к а. В этом случае пишут

или a_n→a при .

Св-ва:

Т.1. Если посл-ть имеет предел, то он единственный..

Док-во:

Пусть lim a_n=a и lim b_n=b необходимо док-ть что a=b. Пусть ε>0 произвольно по опр. 2. сущ-т n₁:n≥n₁=>|a_n-a|<ε/2, сущ-т n₂:n≥n₂=>|a_n-b|<ε/2. Обозначим n₀=max(n₁;n₂), тогда n≥n₀. Будем выполнять оба неравенства. Оценим при таких номерах |a-b|=|(a-a_n)+(a_n-b)|≤|a_n-a|+|a_n-b|<ε/2+ε/2=ε. Получим, что любая ε>0:0≤|a-b|<ε=>|a-b|=0 => a=b

Т2. Если lim х_n=х, lim у_n=у, то lim(х_n + у_n)=х+у, lim(х_n - у_n)=х-у.

Док-во:

Пусть ε>0 произвольно, по опр.2: сущ-т n₁:n≥n₁=>|х_n-х|<ε/2, сущ-т n₂:n≥n₂=>|у_n-у|<ε/2, n₀=max(n₁;n₂), пусть n≥n₀ =>|( х_n у_n)-(х у)|=| (х_n-х) (у_n-у)| ≤|х_n-х| |у_n-у|<ε/2+ε/2=ε.

Опр.3.Посл-ть (a_n) наз-ся БМП, если для любого ε>0 сущ-т n₀:n≥n₀ =>|а_n|<ε

Из опр.2 и опр.3 видим, что БМП сход-ся при чем lim a_n=0.

Из Т.2 получаем БМП БМП=БМП.

Сопоставление опр2 и опр3 показ-т, что lim a_n=a(a_n)= (a_n-a) – БМП.

Отсюда получаем след. представление сход-ся посл-ти lim a_n=a a_n=a+ a_n , где(a_n) - БМП

Опр.4. Посл-ть (a_n) наз-ся ограниченной сущ-т М>0 |а_n|<М для любого n.

Т.3. Каждая сходящаяся послед-ть (в частности и БМП) ограничена.

Т.4. Произведение БМП на ограниченную пос-ть есть БМП.

Следст-е: Произведение двух БМП и произведение БМП на число есть БМП.

Т.5. Предел произведения двух сход-ся посл-й равен произведению их пределов.

lim a_n=a и lim b_n=b => lim a_n b_n =a b.

Док-во:

a_n=a+ a_n , b_n=b+ b_n , где (a_n ) и (b_n ) – БМП. a_nb_n =ab+ab_n+ba_n +a_n b_n =ab+Y_{n .}

(Y_n )-БМП.

Лемма: Если lim b_n=b 0, то (1/ b_n ) – ограниченная посл-ть.

Т.6. Предел частного двух сход-ся посл-й равен частному от деления пределов, при условии что предел знаменателя не ноль.

Док-во:

a_n=a+ a_n , b_n=b+ b_n , где (a_n ) и (b_n ) – БМП.

a_n / b_n –а/b=(1/ b_n )(1/b)( a_nb-a b_n )=(1/ b_n )(1/b)(ab+ a_nb-ab-a b_n)=( Y_n) -БМП

25. Существование верней грани ограниченного сверху множества. Теорема о пределе монотонной послед-ти.

Принцип разделяющей точки: Пусть А и В – не пустые числовые мн-ва, причем для всех и всех выполняется неравенство а≤b. Тогда существует хотя бы одна точка с разделяющая мн-ва А и В, которая обладает след. св-вом (1)

Опр.1.Пусть А-числовое мн-во, число М наз-ся можарантой (минорантой) мн-ва А, если ( ) . Мн-во А имеющее хотя бы одну можаранту (миноранту) наз. ограниченным сверху (снизу).

Опр.2. Если сущ-т наименьшая из можарант (наибольшая из минорант) мн-ва А, то она наз-ся supA (infA).

Т.1. Каждое непустое ограниченное сверху числовое мн-во А имеет наименьшую верхнюю границу (supA).

Док-во: Пусть В – мн-во всех можарант мн-ва А.

В не пустое, т.к. по усл. А ограниченно сверху.

По опр.можаранты .

.Тогда, по ПРТ, найдется хотя бы одно с:

Покажем, что с= supA. Поскольку

-можаранта, -наименьшая можаранта.

Теоремы о гранях применяются в док-ве важной Т. Вейерштрасса о существовании предела у монотонной ограниченной послед-ти чисел. Изложим эту часть материала только для случая возрастающей послед-ти.

Опр.3. Послед-ть (х_n) наз. Возрастающей, если .

Опр.4.Числовая послед-ть (х_n) наз. ограниченной сверху, если существует число М такое, что

Т.2.(Вейштрасса) Каждая возрастающая ограниченная сверху послед-ть (х_n) имеет предел.

Док-во:

В силу ограниченности сверху послед-ти (х_n), получаем что ограниченно сверху мн-во её членов

Тогда по т-ме о гранях последнее мн-во имеет sup: х=sup .

Пусть ε>0 – произвольное положительное число. sup – наименьшая из можарант , поэтому число х-ε уже не будет можарантой для мн-ва . Поэтому

Т.к. посл-ть по усл. Возр-т, то при

Итак имеем Но тогда непременно будет вып-ся или по св-ву модуля х=limx_n.

Двойственным образом док-ся т-ма о том, что сход-ся огранич. Снизу убыв. Посл-ть.