
- •24. Предел последовательности. Арифметические св-ва пределов.
- •25. Существование верней грани ограниченного сверху множества. Теорема о пределе монотонной послед-ти.
- •26. Отображения мн-в (функции). Предел функции в точке. Арифметические св-ва пределов.
- •28. Определение производной функции в точке. Геометрический и механический смысл производной. Правила дифференцирования.
- •29. Дифференцируемость функции и ее дифференциал.
- •30.Теорема Лагранжа и ее применения к исследованию функции.
- •31.Точки mах и min функции. Необходимое условие экстремума. Достаточное условие экстремума.
29. Дифференцируемость функции и ее дифференциал.
Геометрический смысл дифференциала функции в точке.
Пусть
имеем некот. функцию y=f(x)
и пусть t
внутренняя точка её области определения,
если взять
![]() ,
,![]() ,то
мы обозн.
,то
мы обозн.![]() и
будем наз-ть приращением аргумента, а
Δу=f(x)-f(t)
будем называть приращением ф-ии. Заметим
сразу, что если сущ-т
и
будем наз-ть приращением аргумента, а
Δу=f(x)-f(t)
будем называть приращением ф-ии. Заметим
сразу, что если сущ-т
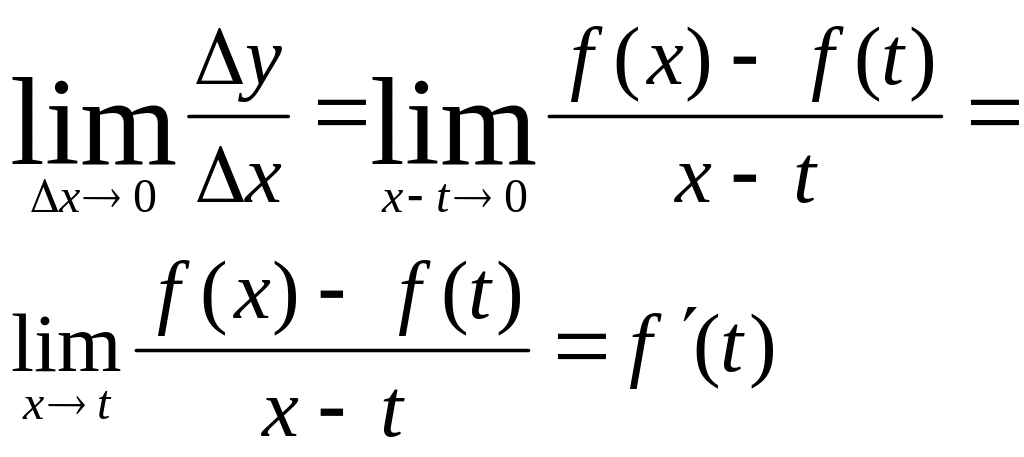
Опр..
Если сущ-т такая постоянная А=const,
что вып-ся рав-во![]() (1), где
(1), где
![]() при
при
![]()
То
говорят что ф-ия y=f(x)
дифференцируема в точке t,
само же выражение
![]() при
этом наз-ся дифференциалом ф-ии в точке
t
и обозн. dy
или df(t).
при
этом наз-ся дифференциалом ф-ии в точке
t
и обозн. dy
или df(t).
Теорема
1.
Для того чтобы ф-ия y=f(x)
была дифференцируемой в точке t
необх. И достат. Чтобы в этой точке сущ-ла
производная
![]() при
чем при выполнении этого условия
р-во(1)имеет место тогда и только тогда,
когда
при
чем при выполнении этого условия
р-во(1)имеет место тогда и только тогда,
когда
![]()
Док-во:
Необходимость.
Пусть
ф-ия диф-ма в точке t,
т.е. выполнено р-во (1). Считая, что
![]() разделим
обе части р-ва (1) на Δх
:
разделим
обе части р-ва (1) на Δх
:![]() .
Устремим
.
Устремим
![]()
![]() и
неоходимость док-на.
и
неоходимость док-на.
Достаточность.
Пусть сущ-т
![]() ,
тогда
,
тогда
![]() .Поскольку
разность между ф-ей и её пределом яв-ся
бесконечно малой
.Поскольку
разность между ф-ей и её пределом яв-ся
бесконечно малой
![]() ,
где
при
.
Умножим все три части последнего р-ва
на
,
где
при
.
Умножим все три части последнего р-ва
на
![]() .Мы
получили р-во (1), в кот.
.Мы
получили р-во (1), в кот.![]() .
.
Произвольное
приращение аргумента принято называть
дифференциалом аргумента
![]() .
Поскольку по опр-ю диф-ла ф-ии
.
Поскольку по опр-ю диф-ла ф-ии
![]()
![]() - дифференциал ф-ии.
- дифференциал ф-ии.
Геом.смысл дифференциала функции.
Выясним
геом-й
смысл диф-ла ф-ии dy
и его связь с приращением ф-ии
![]() .
.
Обозн.![]() и пусть ф-ия диф-ма в точке t.
и пусть ф-ия диф-ма в точке t.
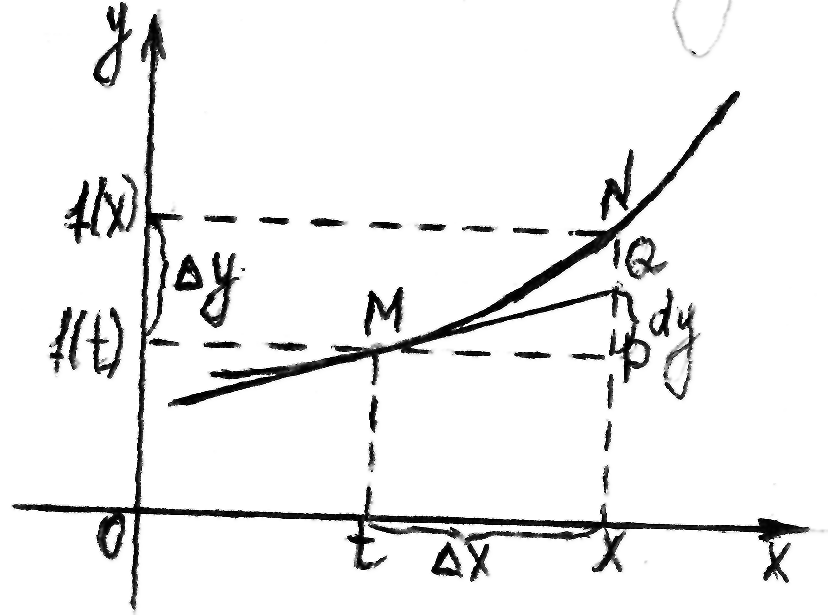
Поскольку
по т-ме ф-ия диф-ма в точке t,
то сущ-т касательная в этой точке. Из
геом. Смысла производной
![]() .
Из
.
Из
![]() MQP:
MQP:
![]() =>
=>
PQ=dy. Т.о. если есть приращение ординаты кривой, то dy есть приращение ординаты касательной к этой кривой проведенной в точке М с абсциссой t.
30.Теорема Лагранжа и ее применения к исследованию функции.
Т. Ролля. Пусть функция f определена на отрезке [а;b] и удовлетворяет трем условиям:
1. функция непрерывна на этом отрезке;
2. функция дифференцируема в интервале (а,b);
3. функция
на концах отрезка имеет одинаковые
значения
f(а)=f(b). Тогда
существует т. с в интервале (а,b)
со св-вом
![]() .
.
Теорема Лагранжа. Если функция f задана на [а;b] и удовлетворяет усл. 1 и 2 теоремы Ролля. Тогда существует т. с в (а,b):
![]()
Док-во:
Мы должны док-ть, что
![]() Составим вспомогательную функцию
Составим вспомогательную функцию![]() .Проверим,что
g(x)
на [а;b]
удов-т усл-м Роля:
.Проверим,что
g(x)
на [а;b]
удов-т усл-м Роля:
1) Эта функция непрерывна на [а;b] как разность непрерывных функций.
2)
![]() в (а;b)
в (а;b)
3)
![]()
![]()
По т-ме
Роля сущ-т с:![]() ,
но
,
но
![]() .
.
Геометрический смысл Т.Лагранжа:
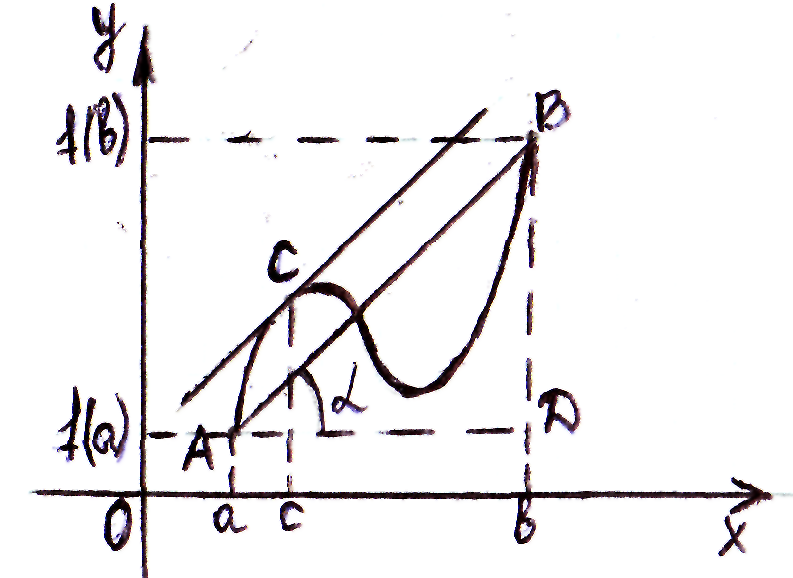
Из
чертежа видно, что
![]() с другой стороны
с другой стороны
![]() -
угловой коэф-т касательной проведенной
в точке С. Рав-во этих двух величин
означает, что касательная параллельна
секущей АВ.
-
угловой коэф-т касательной проведенной
в точке С. Рав-во этих двух величин
означает, что касательная параллельна
секущей АВ.
Итак, на кривой найдется точка в которой касательная параллельна секущей АВ.
Применение теоремы Лагранжа:
Т.1. (Условие постоянства функции):
пусть функция f задана на [а;b] и выполнены условия 1 и 2 т-мы Ролля.
Для
того, чтобы функция была постоянной на
[а;b], необходимо
и достаточно, чтобы![]() для любого х из (а,b).
для любого х из (а,b).
Док-во:
Необходимость.
f(x)=c
=>
![]()
![]()
Достаточность.
Пусть
.
Возьмем произвольно
![]() и
рассмотрим [a,x].
Легко проверяется, что ф-я f
удов-т усл-м т-мы Лагранжа на [a,x]
и
рассмотрим [a,x].
Легко проверяется, что ф-я f
удов-т усл-м т-мы Лагранжа на [a,x]
![]() :
:
![]() Поскольку
Поскольку
![]() =>
=>
![]() =>
=>![]() тогда
f(x)=f(a)=const
тогда
f(x)=f(a)=const
![]()
Т.2. ( условие строгой монотонности )
Пусть функция f задана на [а;b] и выполнены условия 1 и 2 т-мы Ролля.
![]()
![]() Док-во
(для строгого возр-я):
Док-во
(для строгого возр-я):
Возьмем х1,
х2:
![]() и
рассмотрим [х1,
х2 ],
т.к
и
рассмотрим [х1,
х2 ],
т.к
![]() то
усл-я т-мы Лагранжа выполнены на [х1,
х2 ].
Значит
то
усл-я т-мы Лагранжа выполнены на [х1,
х2 ].
Значит
![]() :
:![]() Поскольку
Поскольку
![]() =>
=>
![]() ,
но тогда и
,
но тогда и
![]() .
.
Аналог т-мы 2 яв-ся критерием нестрогой монотонности.
Т.3.(критерий монотонности)
П усть
функция f
задана на [а;b]
и выполнены условия 1 и 2 т-мы
Ролля.
усть
функция f
задана на [а;b]
и выполнены условия 1 и 2 т-мы
Ролля.
![]()
![]()

