3. Отображения мн-в (ф-ии). Предел ф-ии в точке. Арифметические св-ва пределов.
Понятие отображения мн-в в курсе матана вводится чаще всего на основе понятия соответствия, кот. считается первичным и опр-ия не имеет.
О1. Отображением мн-ва А во мн-во В наз. соответствие f, в кот. каждому эл-ту а из А сопост-ся ед. эл-т b из В.
Символ-ая запись:
(отображение “в”) или, коротко f:
A→B.
Мн-во А при этом наз. областью определения отображения f, а эл-ты мн-ва А наз. аргументами отображения f. Элемент b=f(a) из мн-ва В наз. значением отображения f на аргументе а или образом элемента а в отображении f.
Термин ”ф-ия”
применяется как синоним термину
”отображение”. В том случае, когда
мн-ва А и В состоят из ВЧ, т.е.
(подмножества
числовой прямой) вместо термина
“отображения” применяют термин
“числовая ф-ия” или “вещ-ая ф-ия”. Мы
же в этом случае будем говорить: просто
”ф-ия”.
Ф-ии м\т быть заданы таблично, графически, аналитически. В случае аналитического способа задания иногда обл-ть опр-я А не указывается явно. При этом подразумевается, что ф-ия задана на мн-ве всех тех x из R, для кот. данное аналитическое выражение имеет смысл и приводит после выполнения всех указанных операций к числу из R. Область определения ф-ии f в подобном случае будем обозначать D(f).
Например, для фун-и
D(f)=[1;
О2.
Пусть А – непустое числовое мн-во.
Говорят, что а – точка прикосновения
мн-ва А, если существует хотя бы одна
п-ть (an)
со св-ми:
О3.
(Гейне)
Пусть a
– точка прикосновения D(f)
ф-ии f.
Число A
наз. пределом ф-ии f
в точке a,
если для каждой послед-ти аргументов
(хn),
, соответ-щая послед-ть значений функции
Это опр-е позволяет сводить док-во ариф-х св-в пределов ф-и к аналогичным и уже известным ариф-м св-м предела посл-ти.
Обозначение предела
функции f
в точке а:
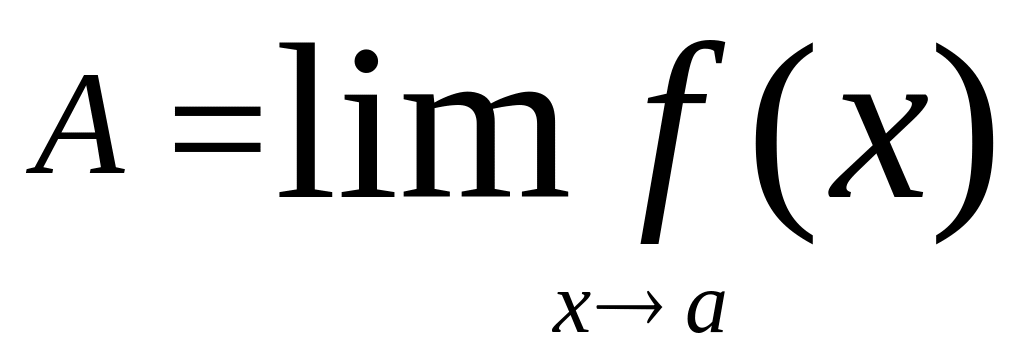
Пример:
Т.1. Если ф-ия имеет предел в точке а, то он ед-ый.
Кр запись:
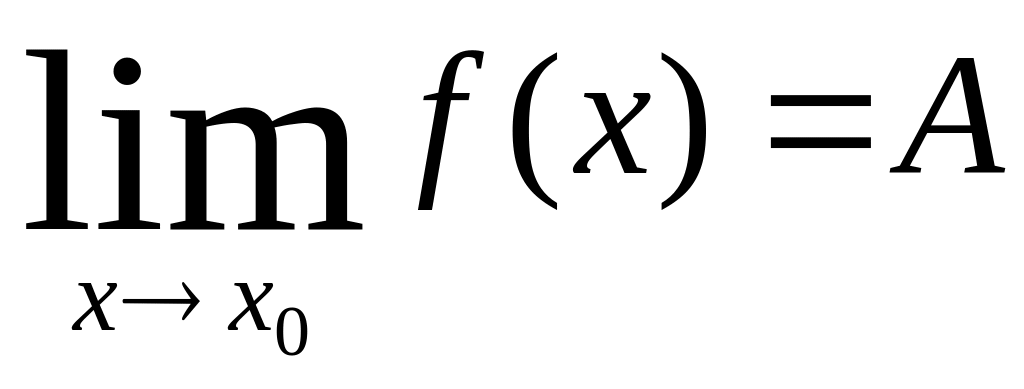
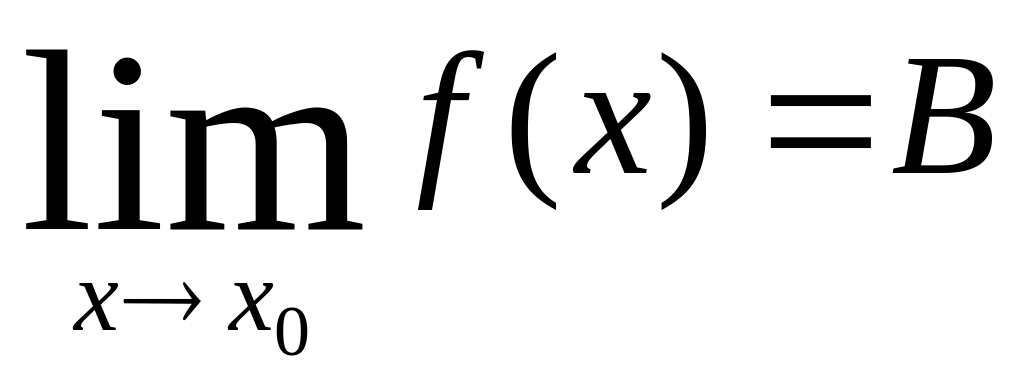
Д-ть, что А=В.
Д-во: Возьмем люб.п-ть (xn), xnЄD(f), xn→а. Тогда по опр.Гейна б\т одновр-но вып-ся f(xn)→А, f(xn)→В. В силу ед-ти предела п-ти А=В.
Т.2.
Пусть
Тогда:
10
Если а – точка прикосн-ия D(f±g)=D(f)∩D(g),
то
20 Если а-точка прикосн-ия D(fg)=D(f)∩D(g), то
30Если
х0-точка
прик-ия D(f/g)=[D(f)∩D(g)]\{x:
g(x)=0},
B≠0,
тогда
Д-во св-в 10 и 30 сходны.
Д-во: Пусть (xn), xnЄD(f/g), xn→а
xnЄD(f)=>f(xn)→A
xnЄD(g)=>g(xn)→B
g(xn)≠0 для люб n
lim(f(xn)/g(xn))=limf(xn)/limg(xn)=A/B чтд.
Т.3. (о локальном сох-и знака)
Если
То найдется такое δ>0: |x- а|<δ, xЄD(f)=>f(x)>0
Опр.4.(Коши) Пусть А точка прикосновения D(f). Число А наз. пределом функции f в точке а, если для любого сколь угодно малого числа ε>0 если вып-но след-е условие:
Т4. Опр-ия пределов ф-ии в точке по Гейне и Коши равносильны.
Д-во: 1) (необх-ть)
По
Гейне, тогда
Пусть ε>0 произвольно,
рассм-м ф-ю g(x)=ε-|f(x)-A|,
тогда
По теор. О локальном сохр-ии знака сущ-ет δ>0: |x-х0|<δ, xЄD(f)=>g(x)=ε-|f(x)-A|>0=>|f(x)-A|<ε
Мы получим, что для люб. ε >0 сущ-ет δ>0: |x-х0|<ε, xЄD(f)=>|f(x)-A|<ε – это опр-е Коши. (Г)=>(K)
2
)
Дост-ть.
По Коши: для любого ε>0 сущ-ет δ>0:|x-х0|<δ, xЄD(f)=>|f(x)-A|<ε
Возьмем для люб. (xn), xnЄD(f), xn→а
По опр-ю предела посл-ти сущ-ет n0: n≥ n0=>|xn- х0|<δ
Из опр-я Коши получим n≥ n0=>|f(xn)-A|<ε=> f(xn)→A
Получаем, для люб. (xn), xnЄD(f), xn→а=> f(xn)→A – это и есть Ур-е Гейне.
(К)=>(Г) чтд