16. Изучение производ-ной функции в средней школе.

Цели темы:

1.Ввести понятие произ-водной функции в точке.

2.Изучить геом-кий и физ-кий смысл производной. 3.Познакомить учащихся с основными правилами дифференцирования. 4.Научить находить производную сложной функции.

5.Ввести формулы произ-водных тригоном-х ф-ций, степенных функций.

6.Научить применять производную при исследо-вании функций.

Содержание: Приращение функции, по-нятие о производной, пра-вила вычисления произ-водной и т.д.

Различные подходы к определению: 1.Логический-(1868-1968)-Определение с помощью предела функции в точке. Вводим определение предела на языке и на языке последова-тельностей. . 2.Исторический(с 1986)

Не изучается понятие пре-дела, но символ может использоваться как замена слову «стремле-ние». Данный подход реа-лизуется в школе.

Введение понятия произ-водной:

1.Башмаков в определении производной использует знак .

2.Колмогоров не исполь-зует этот знак.

Схеме введения и изучение производной.

1.Рассмотреть подводя-щую задачу, раскрыва-ющую физический смысл производной. 2.Сформулировать опр-ие понятия производной. 3.Конкретизировать поня-тие производной (примеры вычисления производной по определению физичес-кого смысла).

4.Рассмотреть приложе-ния производной.

Пример подводящей задачи.

Задача о нахождении мгновенной скорости.

Дано:S=S(t)-зависимость пути от времени.”?”Как охарактеризовать(найти)V в каждый данный момент времени. Для этого воспользуемся понятием средней скорости на АВ: , уменьшаем,

Мгновенная скорость- это число, к которому стремится отношение при стремлении к 0.

1. -фиксированная, выбираем .

2.Находим

3.Путь, пройденный телом

4.

5.

y=f(x),V изменения f в точке-?

1.х₀- фиксированная, возьмем - приращение аргумента:

2.Вычислим

3.Приращение функции

4.Средняя скорость изменения функции

5. называемое производной функции в точке.

Опред: Производной функции f в точке x₀ называется число, к которому стремится разностное отношение

Геометрический смысл производной функции связан с понятием касательной к графику функции в этой точке.

Пусть у=f(x), MN- секущая к графику, k- угловой коэффициент касательной равен .

Применение производной к исследованию функции. Схема:

1.D(f)

2.Исследование на четность. 3.Вычислить производную. 4.Критические точки( ). 5.Промежутки монотонности ( )

6.Точки экстремума

7.График.

Приложения производной:

1.Уравнение касательной:

2.Нахождение числа корней уравнения.

3.Приближенные вычисления:

Следует разделять понятия: производная функции в точке- это число, а производная функции- это некоторая функция, которая обозначается , D₁- мн-во точек, где функция дифференцируема.

17. Изучение первообразной и интеграла в средней школе.

Первообразная и интеграл изучаются в 11 классе.

Содержание:

1.Понятие первообразной функции

2.Основное свойство первообразной

3.Правила нахождения первообр-й.

4.Изучение площади криволинейной трапеции. 5.Интеграл, вычисление, приложение.

Цели:

1.Познакомить учащихся с новой операцией- интегри-рованием.

2.Научить вычислять первообразные.

3.Научить вычислять площадь криволинейной трапеции.

4.Познакомить с понятием интеграла, показать его применение.

Схема изучения первообразной.

1) рассмотрение примеров взаимообратных операций (сложение, вычитание; умножение, деление; возведение в квадрат)

Рассмотрим физическую задачу:

Пусть дано:S=S(t)- прямая. Требуется найти V(t). Ответ: V(t)=S’(t)- операция дифференцирования.

Теперь: пусть дано: V=V(t). Найти S(t). Обратная.

Операция нахождения пути по скорости или нахождение функции по ее производной наз. операци-ей интегрирования. Результатом интегрирова-ния является новая функция- первообразная.

2)Введение интегрирования.

3)Опред: функция F наз. первообразной для ф-ции f на промежутке Х, если

4)Упражнения для закрепления: 1.док-ть, что F(x)первообразная для f(x)(по опред-ю); 2.Какие из данных функций являются первообразными для у=4х³:а)у=х⁴,б)у=х⁴+4, в)у=х⁴-4, г)у=х^-4

Теорема: Множество всех первообразных для функции f на Y имеет вид F(x)+C, где F(x)- одна из первообразных, C-const.

5)Ознакомление учащихся с основным свойством первообразной.

6)Геометрический смысл основного свойства первообразной: графики любых двух первообраз-ных для f получаются друг из друга параллельным переносом вдоль оси (Оу).

7)Составление таблицы первообразных: делают сами учащиеся с опорой на таблицу производных.

8)Ознакомление с правилами первообразной: сумма, разность.

9)Примеры нахожде-ния первообразных.

Изучение теоремы о площади криволинейной трапеции.

у=f(x)- непрерывная, не имеет знака. Опред.: Фигура, ограниченная [a,b] и прямыми х=а и х=b, наз. криволинейной трапецией.

Фрагмент урока:

«Площадь криволинейной трапеции»

1.Подготовительные упражнения(устные): 1упр: дать определение криво-линейной трапеции; 2упр: показать криволинейную трапецию с основанием [a,x], показать ее площадь. «?»Как изменится площадь трапеции, если аргументу х придать приращение .(увеличивается). От выбора точки х зависит площадь. Вывод: на рисунке площадь трапеции представлена как функция S=S(x).

Теорема: Пусть f-непрерывная и неотрица-тельная на [a,b]. S- площадь соответствующей криволинейной трапеции с основанием [a,b], если F- первообразная для f на [a,b], то S=F(b)-F(a) (площадь криволинейной трапеции равна прираще-нию первообразной на [a,b]).

Затем идет док-во этой теоремы.

Введение интеграла.

Рассмотрим другой подход к задаче вычисления площади криволинейной трапеции.

Пусть f- неотрицатель-ная и непрерывная на [a,b] функция. Подсчитаем пло-щадь криволинейной тра-пеции приблизительно следующим образом:

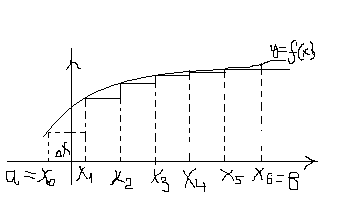
Разобьем [a,b] на n равных частей или n равных отрезков:a=x₀<x₁<x₂<x₃<…<x_n-1<x_n=b; , на каждом из отрезков [x_n-1,x_n] построим прямоугольник со стороной и высотой f(x_n-1). Найдем площади каждого прямоугольника:

При - площадь криволинейной трапеции равна сумме площадей S_n при , стремящейся к некоторому числу. В математике его называют интегралом от функции f.

Получение формулы Ньютона-Лейбница:

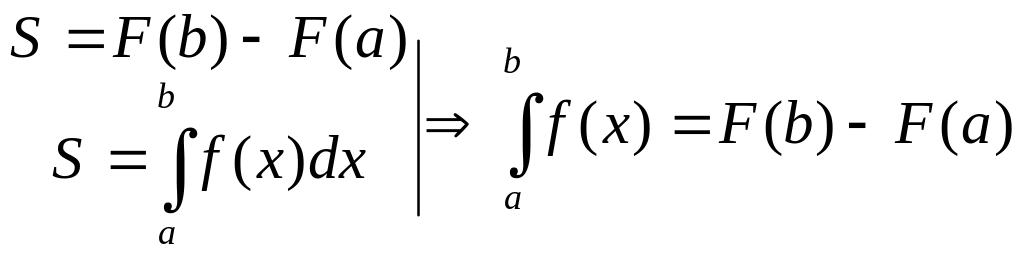Применение интеграла

1.Вычисление объемов тел.

Приложения интеграла (Башмаков).