3.6. Принцип резолюции для логики предикатов

Если в логике высказываний нахождение контрарных пар не вызывает трудностей, то для логики предикатов это не так. Действительно, если мы имеем дизъюнкты типа C₁: P(x)  R(x),

C₂: P(g(y))  Q(y), то резольвента может быть получена только после применения к С₁ подстановки g(y) вместо х.

Имеем C₁: P(g(y))  R(g(y)),

C₂: P(g(y))  Q(y),

C: R(g(y))  Q(y).

Однако для случая

C₁: P(a)  R(x),

C₂: P(g(y))  Q(y), очевидно, никакая подстановка в контрарную пару неприменима и никакая резольвента не образуется. Дадим определение того, что является подстановкой.

Подстановкой будем называть конечное множество вида {t₁/x₁, t₂/x₂, …, t_n/x_n}, где любой t_i – терм, а любая x_i – переменная (1  i  n), отличная от t_i.

Подстановка называется фундаментальной, если все t_i (1  i  n), являются фундаментальными термами. Подстановка, не имеющая элементов, называется пустой подстановкой и обозначается через .

Пусть  = {t₁/x₁, t₂/x₂, …, t_n/x_n} – подстановка и W – выражение. Тогда W будем называть примером выражения W, полученного заменой всех вхождений в W переменной x_i (1  i  n), на вхождение терма t_i. W будет называться фундаментальным примером выражения W, если  – фундаментальная подстановка.

Например, применив к W = {P(x, f(y))  Q(z)} фундаментальную подстановку  = {a/x, g(b)/y, f(a)/z}, получим фундаментальный пример W = {P(a, f(g(b)))  Q(f(a))}.

Пусть  = { t₁/x₁, t₂/x₂, …, t_n/x_n} и  = {u₁/y₁, u₂/y₂, …, u_m/y_m} – две подстановки. Тогда композицией ◦ двух подстановок  и  называется подстановка, состоящая из множества { t₁/x₁, t₂/x₂, …, t_n/x_n, u₁/y₁, u₂/y₂, …, u_m/y_m}, в котором вычеркиваются все t_i/x_i в случае t_i = x_i и u_j/y_j, если y_j находится среди x₁, x₂, …, x_n.

Пример 3.19.  = {g(x, y)/x, z/y} и  = {a/x, b/y, c/w, y/z}. ◦ = {g(a, b)/x, y/y, a/x, b/y, c/w, y/z} = {g(a, b)/x, c/w, y/z}.

Можно показать, что композиция подстановок ассоциативна, т.е. (◦)◦ = ◦(◦).

Подстановку  будем называть унификатором для множества выражений {W₁, W₂, …, W_k}, если W₁ = W₂ = … = W_k. Будем говорить, что множество выражений {W₁, W₂, …, W_k} унифицируемо, если для него имеется унификатор. Унификатор  для множества выражений {W₁, W₂, …, W_k} называется наиболее общим унификатором (НОУ) тогда и только тогда, когда для каждого унификатора  для этого множества выражений найдется подстановка  такая, что  = ◦.

Пример 3.20. W = {P(x, a, f(g(w))), P(z, y, f(u))}. Тогда  = {z/x, a/y, g(w)/u} есть НОУ, а  = {b/x, a/y, g(c)/u, b/z, c/w} есть унификатор, т.е. {b/x, a/y, g(c)/u, b/z, c/w} = {z/x, a/y, g(w)/u} ◦ {b/z, c/w}.

Опишем теперь алгоритм унификации, который находит НОУ, если множество выражений W унифицируемо, и сообщает о неудаче, если это не так.

1. Установить k = 0, W_k = W, _k = . Перейти к пункту 2.

2. Если W_k не является одноэлементным множеством, то перейти к пункту 3. В противном случае положить  = _k и окончить работу.

3. Каждая из литер в W_k рассматривается как цепочка символов, и выделяются первые подвыражения литер, не являющиеся одинаковыми у всех элементов W_k, т.е. образуется так называемое множество рассогласований типа {x_k, t_k}. Если в этом множестве x_k – переменная, а t_k – терм, отличный от x_k, то перейти к пункту 4. В противном случае окончить работу: W_k не унифицируемо.

4. Пусть _k+1 = _k◦{t_k/x_k} и W_k+1 = W_k {t_k/x_k}.

5. Установить k := k + 1 и перейти к пункту 2.

Пример 3.21. Найти НОУ для W = {P(y, g(z), f(x)), P(a, x, f(g(y)))}.

1. k = 0, ₀ =  и W₀ = W.

2. Так как W₀ не является одноэлементным множеством, то перейти к пункту 3.

3. {y, a}, т.е. {a/y}.

4. ₁ = ₀ ◦ {a/y} =  ◦ {a/y} = {a/y}. W₁ = W₀ {a/y} = {P(a, g(z), f(x)), P(a, x, f(g(a)))}.

5. Так как W₁ опять неодноэлементно, то множество рассогласований будет {g(z), x}, т.е. {g(z)/x}.

6. ₂ = ₁ ◦ {g(z)/x} = {a/y, g(z)/x}. W₂ = W₁ {g(z)/x} = {P(a, g(z), f(g(z))), P(a, g(z), f(g(a)))}.

7. Имеем {z, a}, т.е. {a/z}.

8. ₃ = ₂ ◦ {a/z} = {a/y, g(a)/x, a/z}. W₃ = W₂ {a/z} = {P(a, g(a), f(g(a))), P(a, g(a), f(g(a)))} = {P(a, g(a), f(g(a)))}.

₃ = {a/y, g(a)/x, a/z} есть НОУ для W.

Можно показать, что алгоритм унификации всегда завершается на шаге 2, если множество W унифицируемо, и на шаге 3 – в противном случае.

Если две или более одинаковые литеры (одного и того же знака) дизъюнкта С имеют НОУ , то С называется фактором дизъюнкта С.

Пример 3.22. Пусть C = P(x)  P(g(y))  R(x). Тогда НОУ  = {g(y)/x} и фактор дизъюнкта С = P(g(y))  R(g(y)).

Пусть С₁ и С₂ – два дизъюнкта, не имеющие общих переменных (это всегда можно получить переименованием переменных). И пусть L₁ и L₂ = L₁ – литеры в дизъюнктах С₁ и С₂ соответственно, имеющие НОУ . Тогда бинарной резольвентой для С₁ и С₂ является дизъюнкт вида C = (C₁ - L₁)  (C₂ - L₂). Бинарная резольвента может быть получена одним из четырех способов:

1. резольвента для С₁ и С₂;

2. резольвента для С₁ и фактора дизъюнкта С₂;

3. резольвента для фактора дизъюнкта С₁ и С₂;

4. резольвента для фактора дизъюнкта С₁ и фактора дизъюнкта С₂.

Пример 3.23. Пусть C₁= P(f(g(a)))  R(b), C₂ = P(x)  P(f(y))  Q(y). Тогда C₂ = C₂ = P(f(y))  Q(y) и резольвентой для С₁ и С₂ будет С = R(b)  Q(g(a)) ( = g(a)/y).

Принцип резолюции обладает важным свойством – полнотой, которое устанавливается следующей теоремой.

Теорема 3.7. (Теорема о полноте Дж. Робинсона). Множество дизъюнктов S невыполнимо тогда и только тогда, когда существует вывод принципом резолюции из S пустого дизъюнкта.

Так как исчисление предикатов первого порядка полуразрешимо, то для выполнимого множества дизъюнктов S в общем случае процедура, основанная на принципе резолюции, будет работать бесконечно долго.

Приведем два примера, иллюстрирующих принцип резолюции для логики предикатов.

Вернемся опять к примеру 3.4. Посылку и отрицание заключения представим в виде следующего набора дизъюнктов:

1. S(y)  C(y),

2. S(b),

3. V(a, b),

4. C(z)   V(a, z).

Дерево вывода имеет следующий вид (Рис.3.4.)

.

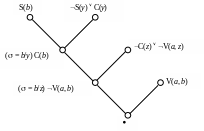
Рис. 3.4.

Пример 3.24. Существуют студенты, которые любят всех преподавателей. Ни один из студентов не любит невежд. Следовательно, ни один из преподавателей не является невеждой.

Запишем эти утверждения на языке логики предикатов и приведем их к виду дизъюнктов:

x (C(x) & y (P(y)  L(x, y)))

x (C(x)  y(H(y)  L(x, y)))

y (P(y)  L(y))

Здесь C(x) – x есть студент;

P(x) – x есть преподаватель;

H(x) – x есть невежда;

L(x, y) – x любит у.

ССФ первой посылки имеет вид: y (C(a) & (P(y)  L(a, y))).

ССФ второй посылки имеет вид: xy (C(x)  H(y)  L(x, y)).

ССФ отрицания заключения имеет вид: y (P(y)  H(y)) =

y (P(y)  H(y)) = y (P(y) & H(y)) = P(b) & H(b).

Таким образом, имеем следующий набор дизъюнктов:

1. C(a),

2. P(y)  L(a, y),

3. C(x)  H(y)  L(x, y),

4. P(b),

5. H(b).

Дерево вывода представлено на Рис. 3.5.

Рис. 3.5 .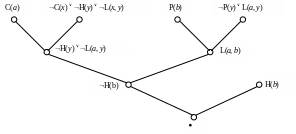

Принцип резолюции является более эффективной процедурой, нежели процедура вывода Эрбрана. Но и он страдает существенными недостатками, заключающимися в формировании всевозможных резольвент, большинство из которых оказывается ненужными. Многочисленные модификации принципа резолюции направлены на нахождение более эффективных стратегий поиска нужных дизъюнктов.

Отметим, что основными способами устранения причин «экспоненциального взрыва», имеющего место при доказательстве теорем практической сложности, являются использование семантики, различных эвристик и встраивание в правила вывода и алгоритмы унификации специфики конкретной предметной области.

Как правило, будем удалять из рассмотрения порождаемые дизъюнкты типа тавтологий, так как невыполнимое множество дизъюнктов, содержащее дизъюнкт-тавтологию, остается снова невыполнимым после его удаления.

Аналогично будем вычеркивать поглощенные дизъюнкты, которые также не меняют невыполнимость множества дизъюнктов. Дизъюнкт С₁ поглощает дизъюнкт С₂ тогда и только тогда, когда имеется подстановка , такая, что С₁  С₂. Дизъюнкт С₂ называется поглощенным дизъюнктом. Например, пусть C₁ = P(x) и C₂ = P(а)  R(y). Если  = {a/x}, то С₁ = P(a). Тогда P(a)  P(a)  R(y), и С₁ поглощает С₂, т.е. С₂ можно без ущерба для вывода вычеркнуть.

Также будем удалять так называемые чистые (pure) дизъюнкты. Литера, чье отрицание отсутствует во множестве дизъюнктов, называется чистой. Дизъюнкт, содержащий чистую литеру, естественно, не может участвовать в выводе пустого дизъюнкта и поэтому он может быть удален из множества дизъюнктов.

В настоящее время известно огромное число модификаций принципа резолюции. Приведем некоторые из них:

• семантическая резолюция (положительная гиперрезолюция, отрицательная гиперрезолюция, стратегия множества поддержки);

• линейная резолюция (её частный случай : входная резолюция для хорновских дизъюнктов);

• OL-резолюция;

• резолюция Connection-Graph (граф соединений)

и т. д.

Все модификации принципа резолюции направлены на уменьшение числа порождаемых лишних дизъюнктов в процессе получения пустого дизъюнкта и на нахождение более эффективных стратегий поиска нужных дизъюнктов.

Задачи. Доказать утверждения п.2.3.(II), используя принцип резолюции для логики предикатов. Построить деревья вывода.