3.5. Принцип резолюции для логики высказываний

Основная идея принципа резолюции заключается в проверке, содержит ли множество дизъюнктов S пустой (ложный) дизъюнкт . Если это так, то S невыполнимо. Если S не содержит , то следующие шаги заключаются в виде новых дизъюнктов до тех пор, пока не будет получен  (что всегда будет иметь место для невыполнимого S). Таким образом, принцип резолюции рассматривается как правило вывода, с помощью которого порождаются новые дизъюнкты из S.

По существу принцип резолюции является расширением modus ponens на случай произвольных дизъюнктов с любым числом литер. Действительно, имея P и P  Q, что равносильно P  Q, можно вывести Q путем удаления контрарной пары P и P. Расширение состоит в том, что если любые два дизъюнкта С₁ и С₂, имеют контрарную пару литер (P и P), то, вычеркивая ее, мы формируем новый дизъюнкт из оставшихся частей двух дизъюнктов. Этот вновь сформированный дизъюнкт будем называть резольвентой дизъюнктов С₁ и С₂.

Пример 3.16. Пусть

C₁: P  Q  R,

C₂: P  Q.

Тогда резольвента С: Q  R.

Обоснованность получения таким образом резольвенты вытекает из следующей теоремы.

Теорема 3.6. Резольвента С, полученная из двух дизъюнктов С₁ и С₂, является логическим следствием этих дизъюнктов.

Если в процессе вывода новых дизъюнктов мы получим два однолитерных дизъюнкта, образующих контрарную пару, то резольвентой этих двух дизъюнктов будет пустой дизъюнкт .

Таким образом, выводом пустого дизъюнкта  из невыполнимого множества дизъюнктов S называется конечная последовательность дизъюнктов С₁, С₂, …, С_k такая, что любой C_i (i =  ) является или дизъюнктом из S, или резольвентой, полученной принципом резолюции, и С_k  = .

Вывод пустого дизъюнкта может быть наглядно представлен с помощью дерева вывода, вершинами которого являются или исходные дизъюнкты, или резольвенты, а корнем – пустой дизъюнкт.

Пример 3.17. Пусть S: 1. P  Q,

2. P  Q,

3. P  Q,

4. P  Q.

Тогда резольвентами будут: 5. Q (1, 2),

6. Q (3, 4),

7.  (5, 6).

Дерево вывода представлено на Рис. 3.1.

Р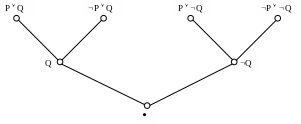 ис. 3.1.

В заключение приведем пример вывода формулы из множества посылок принципом резолюции. Напомним, что доказательство вывода формулы G из множества посылок F₁, F₂, …, F_n сводится к доказательству противоречивости формулы F₁ & F₂ & … & F_n & G (процедура опровержения).

Снова рассмотрим пример 3.10. Имеем следующее множество дизъюнктов:

1. P  Q,

2. Q  R,

3. R  L,

M  L, и отрицание заключения (P  M)

4. P,

5. M.

Д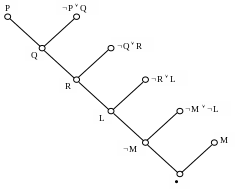 ерево вывода представлено на Рис. 3.2.

Рис. 3.2.

Пример 3.18.

Докажем заключение примера 2.3, используя принцип резолюции.

Доказательство вывода формулы G из множества посылок F₁, F₂, ... , F_n сводится к доказательству противоречивости формулы F₁&F₂&...&F_n&G (процедура опровержения).

Напишем посылки и заключение в форме дизъюнктов.

1. (A&B)(AB)

2. A(B(AB) разъединение посылок

3. A,B (AB) теорема дедукции

Получим следующее множество дизъюнктов.

1. A

2. B

_____________________

3.  (AB)= AB

4. B (1,3)

5.  (2,4)

Дерево вывода представлено на рис. 3.3.

A AB

В

B



Рис. 3.3.

Задачи. Доказать утверждения п.2.2.2. (IV), используя принцип резолюции для логики высказываний. Построить деревья вывода.