3.4. Процедура вывода Эрбрана

Ранее мы установили, что множество дизъюнктов S невыполнимо тогда и только тогда, когда оно принимает значение ложь при всех интерпретациях на любых областях. Однако в силу невозможности рассмотрения всех интерпретаций на любых областях хорошо бы найти такую специальную область интерпретации, установив на которой факт невыполнимости множества дизъюнктов, можно было бы сделать вывод о невыполнимости этого множества на любых других областях интерпретаций.

Такая область, к счастью, имеется, и она называется универсумом Эрбрана. Определим его.

Пусть Н₀ – множество констант, появляющихся во множестве дизъюнктов S. Если в S нет констант, то в Н₀ включается некоторая константа, например, Н₀ = {a}. Для i = 1, 2, … H_i+1 = H_i  {fⁿ(t₁, t₂, …, t_n)}, где fⁿ – все n-местные функциональные символы, встречающиеся в S, а t₁, t₂, …, t_n – элементы множества H_i. Тогда будем Н = Н_ называть универсумом Эрбрана для S, а H_i – его уровнем i.

Пример 3.11. Пусть S = {P(x, a, g(y))  Q(x), P(f(x), a, y)  Q(a)}. Тогда H₀ = {a};

H₁ = {a, f(a), g(a)};

H₂ = {a, f(a), g(a), f(f(a)), f(g(a)), g(f(a)), g(g(a))};

…

H_ = {a, f(a), g(a), f(f(a)), …}.

Пример 3.12. Пусть S = {Q(x)  R(y), P(y)  Q(x)}. Тогда H = H₀ = H₁ = … = H_ = {a}.

Если под выражением понимать терм, множество термов, атом, множество атомов, литеру, множество литер, дизъюнкт или множество дизъюнктов, то под фундаментальным выражением будем понимать выражение, в котором все переменные заменены элементами универсума Эрбрана. Так, фундаментальным примером дизъюнкта будем называть дизъюнкт, полученный заменой всех переменных в этом дизъюнкте элементами универсума Эрбрана таким образом, что все вхождения одной и той же переменной в дизъюнкт заменяются одним и тем же элементом универсума.

Множество фундаментальных атомов вида Pⁿ(t₁, t₂, … t_n), где Pⁿ – все n-местные предикатные символы, встречающиеся во множестве дизъюнктов S и t₁, t₂, … t_n – элементы универсума Эрбрана, называется атомарным множеством или эрбрановской базой для S. Обозначим Эрбрановскую базу через А.

Пример 3.13. Пусть S = {Q(x), P(f(x))  Q(x)}. Тогда H = {a, f(a), f(f(a)), …}, A = {Q(a), P(a), Q(f(a)), P(f(a)), Q(f(f(a))), …}.

Фундаментальные примеры: Q(a), P(f(a))  Q(a) и т.п.

Определим теперь интерпретацию на универсуме Эрбрана и назовем ее Н-интерпретацией. Говорят, что интерпретация I_H является Н-интерпретацией для множества дизъюнктов S, если выполнены следующие соответствия:

• каждому предикатному символу соответствует некоторое n-местное отношение в Н;

• каждому функциональному символу 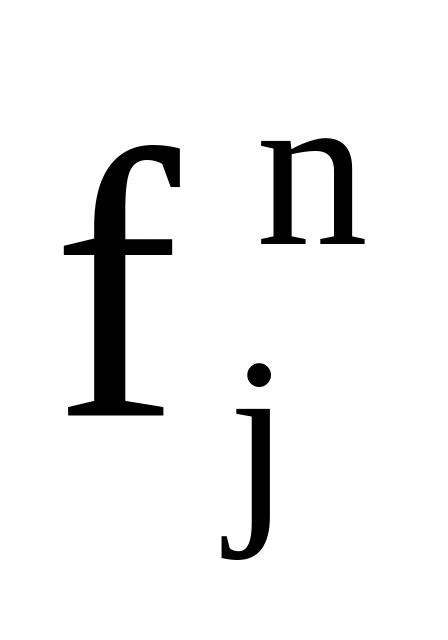соответствует некоторая n-местная функция в Н (т.е. функция отображающая Нⁿ в Н);

• каждой предметной константе a_i из S соответствует некоторая константа из Н (т.е. все константы отображаются на самих себя).

Пусть A = {A₁, A₂, …, A_k, …} является эрбрановской базой для S. Тогда Н-интерпретация I_H может быть представлена множеством I_H = {m₁, m₂, …, m_k, …}, в котором m_j есть A_j или A_j для j = 1, 2, … При этом, если m_j есть A_j, то A_j имеет значение И, в противном случае – Л.

Пример 3.14. Пусть S= {P(f(x))  Q(x), R(x)}. Тогда H = {a, f(a), f(f(a)), …}. A = {P(a), Q(a), R(a), P(f(a)), Q(f(a)), R(f(a)), …}.

Примеры Н-интерпретаций: = {P(a), Q(a), R(a), P(f(a)), Q(f(a)), R(f(a)), …}, = {P(a), Q(a), R(a), P(f(a)), Q(f(a)), R(f(a)), …}, = {P(a), Q(a), R(a), P(f(a)), Q(f(a)), R(f(a)), …}.

При оба дизъюнкта выполнимы, при первый дизъюнкт выполним, второй нет, при оба дизъюнкта невыполнимы, т.е. принимают значение Л.

В случае если интерпретация задана не на универсуме Эрбрана, а на произвольной области D, то можно установить следующее соответствие между этими интерпретациями. Пусть дана интерпретация I на некоторой области D. Говорят, что Н-интерпретация I_H соответствует интерпретации I, если имеет место следующее: пусть h₁, h₂, …, h_n, … – элементы Н и пусть каждый h_i отображается на некоторый элемент d_i области D, тогда, если любой P(d₁, d₂, …, d_n) принимает значение И (Л) при интерпретации I, то P(h₁, h₂, …, h_n) также принимает значение И (Л) при I_H. Имеет место следующая теорема.

Теорема 3.4. Множество дизъюнктов S невыполнимо тогда и только тогда, когда S ложно при всех Н-интерпретациях.

Доказательство «тогда» очевидно, а «только тогда» легко доказывается от противного введением соответствия между Н-интерпретацией и некоторой произвольной интерпретацией. В дальнейшем будем рассматривать только Н-интерпретации, и называть их просто интерпретациями I.

Таким образом, для установления невыполнимости множества дизъюнктов необходимо и достаточно рассмотреть только Н-интерпретации.

Процедура вывода Эрбрана основывается на его теореме.

Теорема 3.5. (теорема Эрбрана). Множество дизъюнктов S невыполнимо тогда и только тогда, когда существует конечное невыполнимое множество S фундаментальных примеров дизъюнктов S.

Таким образом, для установления невыполнимости множества дизъюнктов необходимо образовать множества S₁, S₂, …, S_n фундаментальных примеров дизъюнктов и последовательно проверять их на ложность. Теорема Эрбрана гарантирует, что, если множество дизъюнктов S невыполнимо, то данная процедура обнаружит такое n, что S_n является ложным.

Процедура вывода Эрбрана состоит из двух этапов: сначала находится множество всех фундаментальных примеров дизъюнктов и затем, используя мультипликативный метод, из КНФ получают ДНФ.

Пример 3.15. Пусть S = {P(x)  Q(x, g(x)), P(f(a)), Q(y, z)}. Находим H = {a, f(a), g(a), f(f(a)), f(g(a)), g(f(a)), g(g(a)), …} и фундаментальные примеры дизъюнктов: S₁₀ = {P(f(a))  Q(f(a), g(f(a))), P(f(a)), Q(f(a), g(f(a)))}. Затем с помощью мультипликативного метода убеждаемся в невыполнимости S: (P(f(a))  Q(f(a), g(f(a)))) & P(f(a)) & Q(f(a), g(f(a))) = P(f(a)) & P(f(a)) & Q(f(a), g(f(a)))  Q(f(a), g(f(a))) & P(f(a)) & Q(f(a), g(f(a))) =    = .

Недостаток процедуры вывода Эрбрана состоит в экспоненциальном росте множестве фундаментальных промеров S_i при увеличении i. Мультипликативный метод, использованный Гилмором при машинной реализации этой процедуры, также неэффективен. Как легко видеть, даже для малого множества из десяти двухлитерных фундаментальных промеров дизъюнктов существует 2¹⁰ конъюнкций в ДНФ. Вот почему Гилмор смог доказать только простые теоремы. Иной поход предложил Дж. Робинсон, который ввел принцип резолюции, являющийся теоретической базой для построения большинство методов автоматического доказательства теорем.