1.6. Целочисленное линейное программирование. Метод Гомори

Если управляющие переменные в задаче линейного программирования определяют количество единиц неделимой продукции, то оптимальное решение должно быть получено в целых числах. К задачам такого типа относится большое число экономических задач, например распределение производственных заказов между предприятиями, оптимальный раскрой материалов, определение загрузки оборудования, распределение транспортных средств по рейсам, задачи производства и реализации неделимой продукции. Если единица составляет малую часть от общего количества, например при планировании массового и крупносерийного производства, то для нахождения оптимального решения применяют обычный симплекс-метод и округляют полученное решение до целого. В противном случае, например при планировании производства или реализации автомобилей, округление может привести к решению, далекому от оптимального. Линейные задачи, решение которых должно быть получено в целых числах, называют задачами целочисленного программирования (ЦЛП).

Математическая модель задачи ЦЛП имеет следующий вид:

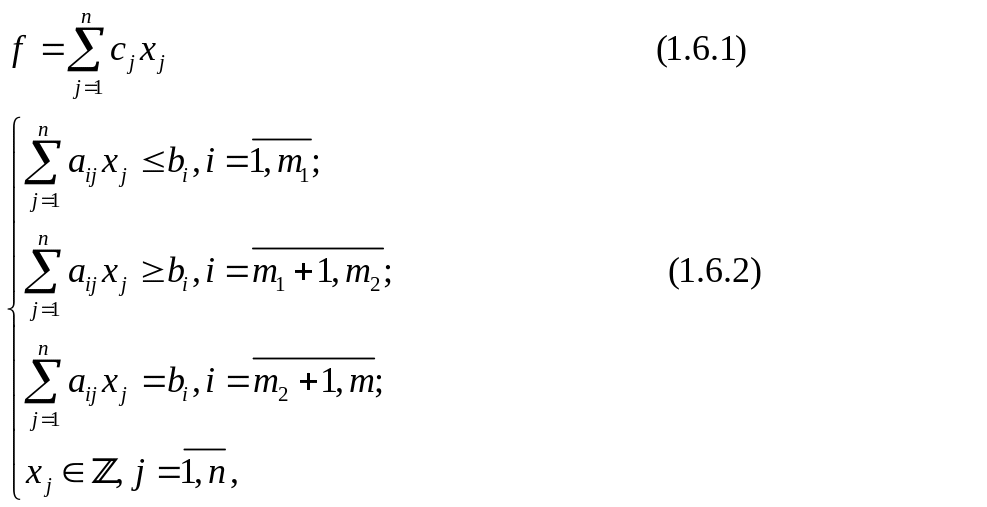
где — множество целых чисел.

Для решения задачи ЦЛП может быть применен метод Гомори. Метод Гомори содержит два этапа.

1. Решение исходной задачи обычным симплекс-методом и проверка решения на целочисленность. Если решение содержит хотя бы одно дробное значение, то переходят к этапу 2, в противном случае расчет заканчивается.

2. Составление дополнительного ограничения (сечения) и решение расширенной задачи обычным симплекс-методом. Дополнительное ограничение отсекает целочисленные решения.

Сечение обладает следующими двумя свойствами:

1. любое целочисленное решение ему удовлетворяет;

2. любое нецелочисленное решение задачи ему не удовлетворяет.

Объясним, как составляется сечение.

Пусть выполнен этап 1.

— дробное число.

Рассмотрим -ое ограничение:

.

Так как — дробное число, а в правой части все переменные целые, то хотя бы одно значение должно быть дробным.

Возьмем дробную часть от левой и правой частей ограничения. Обозначим через дробную часть числа .

Дробная часть суммы не превосходит суммы дробных частей слагаемых, поэтому .

Дробная часть произведения не превосходит произведения целого на дробную часть, следовательно:

В результате имеем: .

Обозначим

Тогда из последнего неравенства получаем:

.

Отняв от левой части неравенства дополнительную неотрицательную переменную, переходим к уравнению

При дополнении этого ограничения к исходной задаче мы получили задачу большей размерности. Эту задачу решают обычным симплекс-методом, т.е. переходят к этапу 1. Если при решении задачи симплекс-методом имеется несколько дробных решений, то дополнительные ограничения следует составлять для значения, имеющего максимальную дробную часть.

Глава 2. Специальные задачи линейного программирования

2.1 Построение транспортной модели

Построим транспортную модель для конкретной задачи.

Пример 2.1.1

Четыре предприятия данного экономического района для производства продукции используют некоторое сырье. Спрос на сырье каждого из предприятий соответственно составляет: 120, 50, 190 и 110 усл. ед. Сырье сосредоточено в трех местах. Предложения поставщиков сырья равны: 160, 140 и 170 усл. ед. На каждое предприятие сырье может завозиться от любого поставщика. Тарифы перевозок известны и задаются матрицей:

.

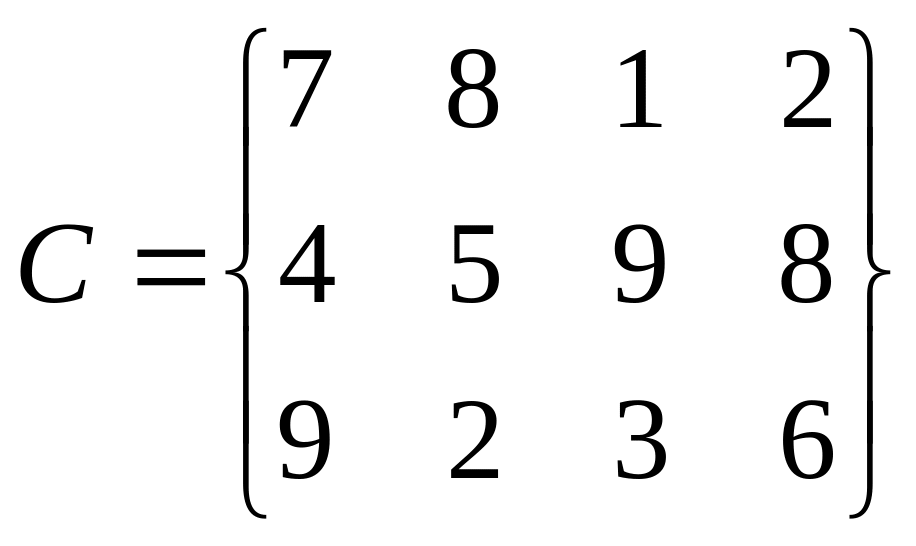В -ой строке -ом столбце матрицы стоит тариф на перевозку сырья от -ого поставщика -ому потребителю, . Под тарифом понимается стоимость перевозки единицы сырья.

Требуется составить план перевозок, при котором общая стоимость перевозок минимальна.

Построение математической модели.

Цель задачи состоит в минимизации суммарной стоимости на перевозки. Эта цель может быть достигнута с помощью оптимальной организации перевозок сырья. Следовательно, за неизвестные можно принять количество сырья, перевозимого от каждого поставщика каждому потребителю.

Пусть — количество сырья, перевозимого от -ого поставщика -ому потребителю. Параметры задачи — число поставщиков и потребителей, предложение и спрос сырья в каждом пункте, тарифы на перевозки.

Ограничения задачи — это ограничения на предложение и спрос сырья. Предложения сырья всех поставщиков не должны быть меньше суммарного спроса на него во всех пунктах потребления. В данной задаче имеет место точное равенство между предложением и спросом.

120+50+190+110=160+140+170=470.

Количество сырья, вывозимого от каждого поставщика, должно быть равно наличному количеству сырья. Количество сырья, доставленное каждому потребителю, должно равняться его спросу. Последнее ограничение — условие неотрицательности .

Критерием эффективности (целевой функцией) являются суммарные затраты на перевозку, равные сумме произведений тарифов на перевозку на количество перевозимого сырья от каждого поставщика каждому потребителю.

Окончательно математическая модель задачи имеет вид:

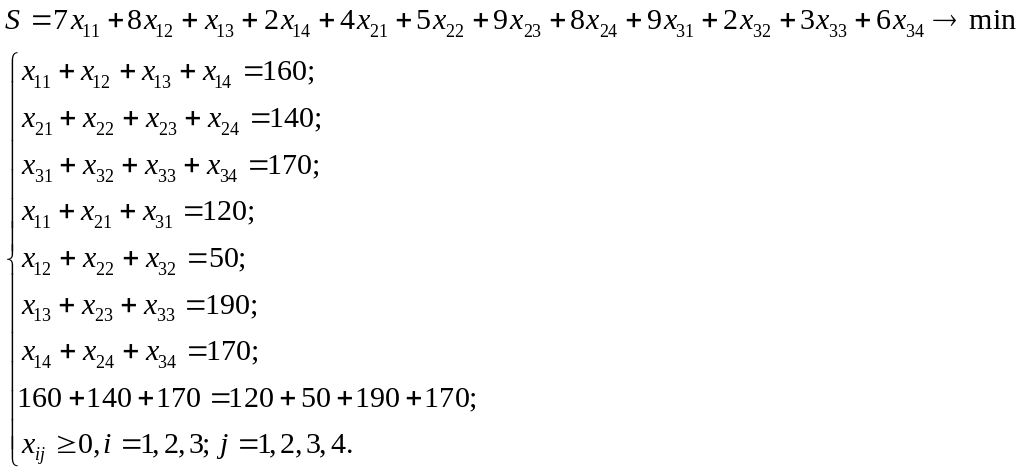
Целевая функция и ограничения линейны, т.е. данная задача относится к задачам линейного программирования, однако, благодаря особой структуре, эта задача получила специальное название: транспортная задача или транспортная модель.