Принцип отражения и числа Каталана
Попробуем применить принцип отражения для вычисления значений чисел Каталана. Для этого нам нужно оценить количество хождений по треугольнику Паскаля до линии c номером 2n, при которых выигрыш первого игрока всегда не меньше нуля, а в конце равен нулю.
Сделать это непосредственно не получается, так как все три “выигрыша” — и начальный, и конечный, и промежуточный, соответствующий границе, которую мы не должны пересекать, одинаковы и равны нулю.
Решить задачу можно следующим образом. В любом интересующем нас случае первое бросание монеты должно оканчиваться выпадением орла, поэтому достаточно рассматривать лишь пути, выходящие из точки, находящейся на первом (а не на нулевом) ряду правее начальной. Наша задача описывается хождениями по треугольнику Паскаля, начинающимися в точке справа в первом ряду. Но можно представить себе, что эта точка является началом своего (нового) треугольника Паскаля, по которому мы и ходим. Тогда наша задача легко сводится к следующей задаче.
Задача. Сколько существует возможных исходов (2n-1) бросаний монеты, после которых второй игрок, не выигрывая по ходу игры двух или более рублей, в конце игры будет иметь выигрыш один рубль?
Эта задача уже напрямую решается с помощью метода отражений. Для этого нужно посчитать количество всех исходов, при которых второй игрок выиграет рубль, и вычесть количество исходов, при которых второй игрок выиграет три рубля. Оба этих числа стоят в (2n-1)–й строке треугольника Паскаля.
В итоге получим еще одну формулу для чисел Каталана:
(7)
И действительно, 1=1-0, 2=3-1, 5=10-5, 14=35-21, 42=126-84, 132=462-330, …
Теперь можно легко вывести “старую формулу” для чисел Каталана:
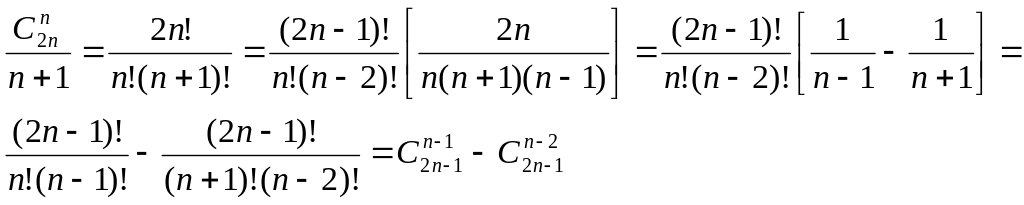
Упражнение.
Покажите, что верна формула
Распределение времени выигрыша
Зададим читателю один естественный и на первый взгляд очень простой вопрос. Пусть двое играют в орлянку и бросают монету достаточно много раз (N). Какую–то часть времени выигрывает первый игрок, какую–то часть времени второй. Для большей точности скажем, что между двумя последовательными моментами бросания монеты в выигрыше находится тот игрок, который либо до, либо после бросания монеты выигрывал (т.е. если сначала у первого игрока выигрыш был ноль, а затем стал равен единице, то считается, что на таком промежутке времени выигрывает первый игрок). Будем считать, что игра длится одну единицу времени, а монета бросается с одинаковой частотой. Получим некоторое отношение выигрышей: время t в выигрыше находится первый игрок, время 1-t в выигрыше находится второй игрок. При всевозможных N–кратных бросаниях монеты будут выпадать разные пары (t,1-t). Какие распределения выигрыша по времени встречаются наиболее часто?
Неискушенный в теории вероятностей и игре в орлянку читатель возможно скажет, что скорее всего примерно половину времени в выигрыше будет находиться один игрок и примерно половину времени другой.
И будет не прав! На самом деле ответ прямо противоположный. Наиболее вероятно, что почти все время в выигрыше находится один из игроков — либо первый, либо второй. Смена лидерства — очень редкое явление.
Процитируем здесь фразу из предисловия к знаменитому учебнику по теории вероятностей В. Феллера [2]:
“Результаты, связанные со случайными колебаниями при бросании монеты, показывают, что широко распространенное представление о законе больших чисел ошибочно. Эти результаты столь неожиданны и в такой степени не согласуются с обычной интуицией, что даже искушенные люди сомневались, что монета ведет себя в самом деле так плохо, как предсказывает теория”.
Приведем лишь одно утверждение, из которого все станет ясно. Пусть бросание монеты происходит 2n раз (без ограничения общности можно считать, что наше очень большое число бросаний является четным).
Какова вероятность того, что все время первый игрок будет находиться в выигрыше?
Всего
количество различных исходов бросания
монеты равно
.
Количества исходов, соответствующие
постоянному выигрышу первого игрока
считаются с применением принципа
отражения. Если его конечный выигрыш
будет равен нулю, то, как мы знаем, мы
получим число Каталана, равное
.
Если конечный выигрыш первого игрока
равен единице, то по тому же принципу
отражения нам нужно рассмотреть разность
двух других чисел в (2n-1)–й
строке треугольника Паскаля:
.
Если окончательный выигрыш равен двум,
то мы получим
,
и так далее. В итоге получим сумму
элементов (2n+1)–й
строки треугольника Паскаля, при которой
все элементы, кроме двух центральных,
сокращаются по симметричности, а эти
центральные и дают искомую сумму:
.
Таким
образом, количество исходов, при которых
первый игрок выигрывает все время, равно
.
При различных исходах 2n–кратного
бросания монеты первый игрок может
находиться в выигрыше все время (т.е.
1),
часть времени,
частей времени (нетрудно заметить, что
количество долей времени, в течении
которых выигрывает один игрок, обязательно
четно). Все эти случаи встречаются с
некоторой частотой. Как мы только что
сосчитали, первый игрок постоянно
выигрывает в
случаях.
Из соображений симметричности то же
можно сказать и о случаях постоянного
лидерства второго игрока.
Пусть
для четного числа 2k<2n
число A(k)
означает количество случаев, когда
первый игрок выигрывает в течении
единиц времени и проигрывает оставшееся
время.
Чуть более сложно можно доказать следующую формулу (мы этого делать не будем, желающие могут найти подробное доказательство в учебнике Феллера):
(8)
Покажем, что величина A(k) достигает максимума при k=0 и k=n, т.е. когда один из игроков выигрывает все время. Действительно, при значениях k, отличных от нуля, формула (8) показывает, что A(k) равно количеству путей на треугольнике Паскаля, идущих от начала до середины (2k)–й строки, умноженное на количество путей, идущих от начала до середины (2n-2k)–й строки. Это же количество, очевидно, можно трактовать как число путей, выходящих из начала и идущих в середину (2n)–й строки, проходящих через середину (2k)–й строки. В то же время A(0)=A(n) означает число всех путей, идущих из начала и доходящих до середины (2n)–й строки, что очевидно, больше, чем A(k).
Заметим, что число A(k) тем больше, чем дальше находится k от n, и достигает своего максимума при k=0 и k=n.
На
самом деле верно и более сильное
утверждение: функция A(k)
имеет минимум при
если n
четно.
И вообще:
наименее вероятными являются ситуации, при которых игроки выигрывают в течение примерно одинакового времени.