Производящие функции

Мы расскажем о том, как получать явные формулы для последовательностей, определяемых рекуррентными соотношениями, в частности, для чисел Фибоначчи и для чисел Каталана.

Пусть имеется некоторая последовательность чисел a(n), n=0,1,… Запишем формальный ряд (бесконечную сумму) , где t обозначает некоторую формальную переменную, т.е. букву, удобную для записи формальных выражений и произведения операций с ними. Такой ряд называется производящей функцией или генератрисой для последовательности a(n). Так, для чисел Фибоначчи мы получим производящую функцию , а для чисел Каталана — ряд Оказывается, что вычислять такие ряды в целом легче, чем каждый их член по отдельности. Проиллюстрируем это на примере чисел Фибоначчи.

Числа Фибоначчи, золотое сечение и цепные дроби Явная формула для чисел Фибоначчи

Итак, для чисел Фибоначчи (мы их будем обозначать через F(n), нулевой и первый члены равны единице) имеем: F(n+1)=F(n)+F(n-1).Попробуем теперь записать это равенство в терминах S, где S—производящая функция от переменной t для F. Нетрудно заметить, что оно будет выглядеть так:

.

Действительно, умножение на степень переменной t означает сдвиг последовательности вправо, а единица в левой части равенства — свободный член последовательности S(t). Это равенство можно записать еще так:

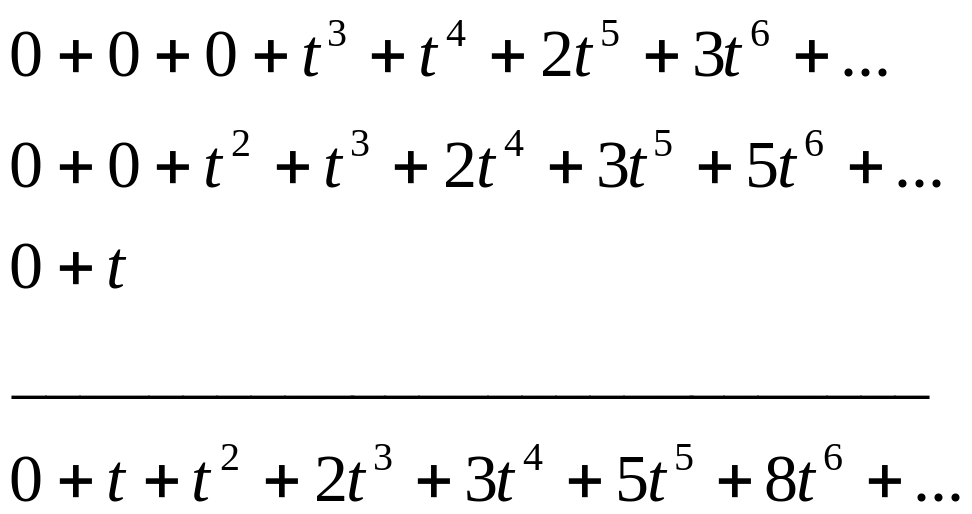
Теперь рассмотрим S(t) как обычную функцию от переменной t и проделаем следующие преобразования:

.

Квадратное уравнение легко решается. Его решения равны . Отсюда следует, что Таким образом,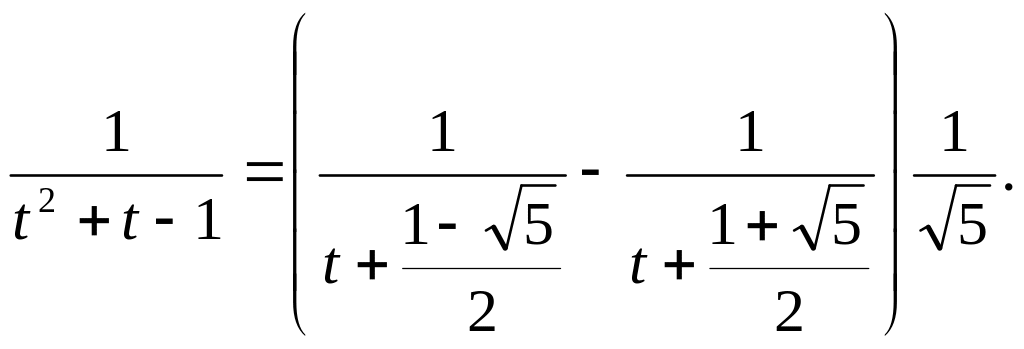

Итак, в правой части у нас стоят дроби, а нам нужен ряд. Как получить этот ряд? Предположим, что k—некоторое малое число. Тогда, как известно, имеет место формула Предположим теперь, что переменная t в производящих функциях — как раз очень маленькое число. Следовательно, мы можем расписать интересующие нас дроби как ряды: .

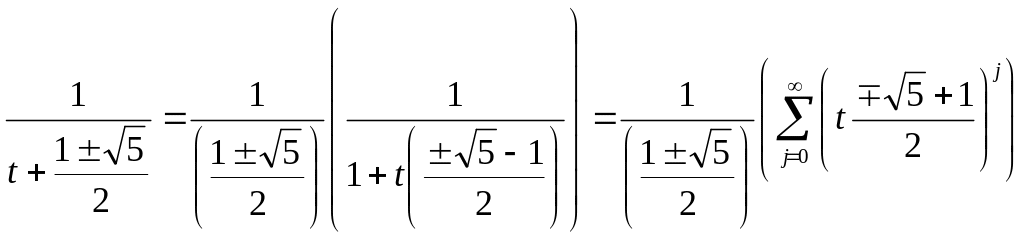Таким образом, получаем окончательную явную формулу для S(t):

,

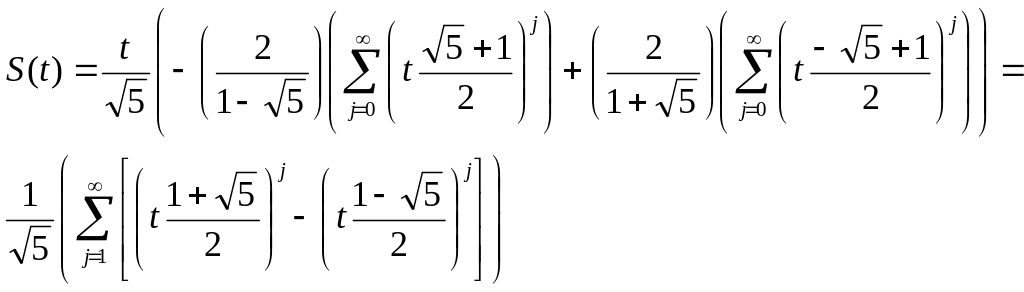которая дает нам явную формулу для вычисления чисел Фибоначчи F(n), где F(n) — коэффициент при n–й степени переменной t для ряда S(t).

Итак, (2).

При этом все числа Фибоначчи являются целыми, т.е. какое бы n мы ни подставили в эту формулу, мы получим целое число, несмотря на присутствующие в формуле корни из пяти.

У чисел Фибоначчи есть замечательное свойство. Давайте напишем первые несколько чисел (нулевое число Фибоначчи по определению считается равным нулю). 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10949, 17711, 28657, 46368, 75625, 121393 … Как видно, каждое пятое число (они выделены красным) делится на пять. Это красивое и простое свойство легко проверяется, если перейти от чисел Фибоначчи к их остаткам от деления на пять. В этом случае мы легко увидим, что они чередуются с периодом двадцать, причем на каждом пятом месте остаток от деления на пять равен нулю: 0,1,1,2,3,0,3,3,1,4,0,4,4,3,2,0,2,2,4,1,0,1,1… Тот факт, что дальше последовательность будет всегда повторяться, объясняется тем, что она полностью определена любыми двумя соседними членами.

При этом свойство делимости на пять каждого пятого члена последовательности Фибоначчи достаточно несложно выводится из (2). Более того, верно и гораздо более сильное утверждение: каждое 25–е число Фибоначчи делится на 25, каждое 125–е — на 125 каждое 625–е — на 625, и т.д, которое также можно проверить, используя явную формулу (2).

Действительно, зафиксируем число n, делящееся на некоторую степень пятерки . Рассмотрим формулу (2). Она состоит из двух слагаемых, каждое из которых — n-я степень некоторого иррационального числа, деленная на . При этом можно считать, что выражения, возводимые в степень, не имеет двойки в знаменателе: умножая выражение (2) на , мы получим некоторое целое число, которое делится на ту же степень пятерки, что и F(n), так как числа Фибоначчи все целые, а два и пять — взаимно простые числа. Для того, чтобы сосчитать эти суммы, воспользуемся известной формулой разложения по биному Ньютона:

,

где в качестве a и b в первом случае будут фигурировать 1 и , а во второй будут 1 и . Для каждого члена каждого из двух биномиальных разложений будем следить за степенью пятерки. Эта степень пятерки складывается из двух степеней, одна из которых происходит от корня из пяти, а вторая — из числа сочетаний из n по m, где m пробегает значения от 0 до l. Легко видеть, что при суммировании биномиальных разложений все члены при четных степенях переменной b сократятся, т.к. для четных значений переменной p. В том числе сократятся и члены при нулевой степени переменной b, которые равны единице каждый. Будем следить за оставшимися членами.

В обоих разложениях каждый член будет представлять собой целое число, умноженное на , а после деления на все числа станут целыми. Вспомним теперь, что наше число n делится на степень пятерки .

Заметим следующий факт. Пусть m — число, делящееся на k–ю степень пятерки (k<l), но не делящееся на (k+1)–ю. Тогда число делится на .

Действительно, по формуле мы имеем . Запишем теперь число . Это число является числом сочетаний, и, следовательно, оно — целое. При этом оно отличается от первого числа ( ) лишь одним сомножителем в числителе: в нем вместо n стоит n-m. Таким образом, (максимальная) степень пятерки, на которую делится ровно настолько больше степени пятерки, на которую делится , насколько степень пятерки, на которую делится n больше степени пятерки, на которую делится число n-m. По определению в n пятерка входит в качестве сомножителя l раз. Число n-m, как и число m, делится лишь на k–ю степень пятерки. Таким образом, количество вхождений пятерки в качестве сомножителя в число не меньше l-k.

Это означает, что в обоих разложениях по биному степеней слагаемое будет равно корню из пяти, умноженному на целое число, делящееся на . Таким образом, эти члены дают вклад, делящийся на . Рассмотрим теперь числа Ясно, что первое из них, не делящееся на , будет , первое число, не делящееся на будет , и т.д. Однако в каждой из двух сумм эти числа, не делящиеся на ту или иную степень пятерки, будут коэффициентами при большой степени корня из пяти. Так, для пятого члена мы получим , для двадцать пятого получим . Следовательно, степень пятерки растет очень быстро за счет корня из пяти, а убывание степени пятерки в числе сочетаний — очень медленное, поэтому каждый член нашей суммы, а, следовательно, и вся сумма, будет делиться на .

Упражнение. Напишите явную формулу, для чисел, каждое следующее из которых равно разнице двух предыдущих, и которые начинаются с 1, 1.

Аналогичным образом можно вычислять явные формулы для последовательностей чисел, в которых каждое следующее выражается через три, четыре предыдущих с некоторыми коэффициентами. Однако для этой цели придется находить корни уже не квадратного уравнения, а кубического или четвертой степени.