Золотое сечение

С древних времен известна задача архитектурного происхождения о нахождении золотого сечения — такого вещественного числа a, чтобы при приклеивании к кирпичу с отношением сторон, равным a, квадратного кирпича мы снова получали кирпич с отношением сторон, равным a,см. рис. 3.

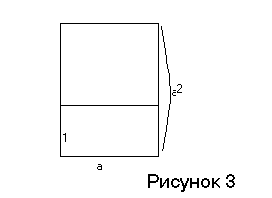
Без труда можно сообразить, что искомое число будет решением квадратного уравнения Корни этого уравнения нам хорошо известны в связи с изучением чисел Фибоначчи. Они равны , а так как число является отрицательным и поэтому длиной кирпича служить не может, то единственным решением этой задачи остается

Рассмотрим последовательные отношения соседних чисел Фибоначчи: Нетрудно заметить, что возрастание этих чисел чередуется с убыванием: При этом интуитивно понятно, что эти отношения к чему–то стремятся. Из рекуррентной формулы (2) для чисел Фибоначчи видно, что числа Фибоначчи являются суммами двух геометрических прогрессий со знаменателями и . При этом знаменатель первой геометрической прогрессии по модулю больше единицы, значит, прогрессия стремится к бесконечности. Знаменатель второй прогрессии, напротив, убывает, следовательно, прогрессия стремится к нулю. Поэтому начиная с некоторого момента последовательность чисел Фибоначчи ведут себя как эта прогрессия, следовательно, искомый предел соотношений равен золотому сечению . Это можно трактовать еще и так: каждый раз прибавляя одно число Фибоначчи к соседнему, мы стремимся получить золотое сечение, и все ближе и ближе к нему подходим, см. рисунок 4.

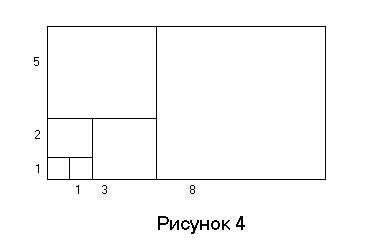
Кстати, приближение золотого сечения числами Фибоначчи дает нам возможность найти сколь угодно точную оценку для числа .

Цепные дроби

Предположим, что у нас есть два взаимно простых натуральных числа p и q — два числа, не имеющих общих делителей. Тогда существуют целые числа r и s такие, что pr+qs=1. Эти числа обычно ищутся с помощью алгоритма Евклида . Берется большее из чисел p и q и с остатком делится на меньшее. Остаток является суммой двух изначальных чисел с целыми коэффициентами. Затем берется меньшее число и остаток и с ними проделывается то же самое. Так как изначальные два числа были взаимно простые, то на каждом шаге мы будем получать два взаимно простых числа и алгоритм можно продолжать. В конце концов, мы дойдем до единицы. Оказывается, этот алгоритм можно формализовать и сделать более наглядным с помощью так называемых цепных дробей. Рассмотрим два взаимно простых числа, например, 100 и 31. Попытаемся найти целые числа r и s такие, что 100r+31s=0. Для этого рассмотрим дробь и будем ее преобразовывать следующим образом: как только возникает дробь, большая единицы, будем выделять из нее целую часть, а остаток обращать. Число, обратное к остатку, снова будет больше единицы, и мы с ним проделаем то же самое. Процесс закончится, когда мы получим целое число. Итак,

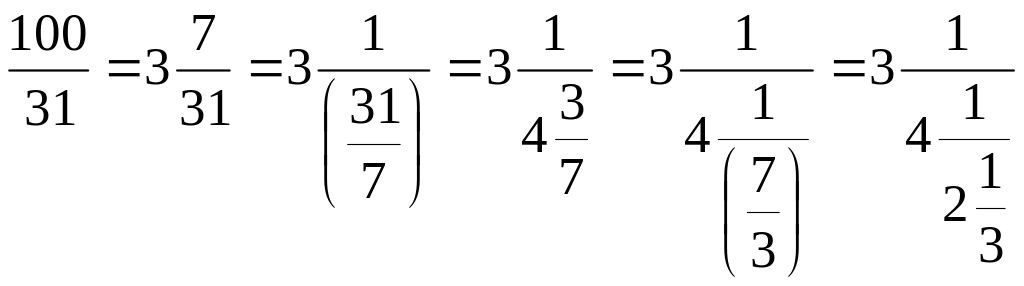
Получившуюся цепную дробь можно обрубить, откинув последний член . Тогда мы получим дробь . Понятно, что мы нашу дробь изменили совсем немного, т.е. . Попытаемся оценить близость этих дробей. Для этого умножим 100 на 9, а 31 на 29. Получим: . Вот и решение! Положив r=9, s=-29, мы в точности получим 100r+31s=1. На самом деле, если действовать так и обрубать последнюю дробь, то изначальная дробь будет либо немного уменьшаться, либо немного увеличиваться, в зависимости от того, на каком “ярусе” мы ее обрубаем — на четном или на нечетном. Так, уменьшение числителя уменьшает дробь, а уменьшение знаменателя — увеличивает. Поэтому, действуя так, как указано выше, мы будем получать pr+qs=1 или pr+qs=-1. В последнем случае решением будет являться пара (-r,-s): -pr-qs=1.

Упражнение. Найдите решение уравнения в целых числах 21r+8s=1.

Как мы видим, любую дробь можно разложить в цепную дробь; при этом процесс завершится. Оказывается, точно так же можно разлагать в цепные дроби и иррациональные числа. В этом случае, очевидно, мы будем получать бесконечную цепную дробь.

Рассмотрим, например, такую дробь:

Она будет стремиться к некоторому числу (иррациональному). Если вычесть из этой дроби единицу, а затем обратить, то получим снова эту же дробь. Обозначим ее через x. Тогда для нахождения значения x нужно решить уравнение или . Ответом будет то самое золотое сечение . Теперь уже видно, что если обрубить эту дробь в каком-нибудь конечном месте, мы получим дробь, выражающую отношение двух соседних чисел Фибоначчи.

Упражнение. Покажите, что для чисел Фибоначчи справедливо равенство для любого натурального n.