8. Представление операторов в матричной форме.

Пусть некоторый оператор А переводит переводит  в :

или .

Разложим обе функции в ряд по собственным функциям _i эрмитова оператора L:

и . Тогда

Ну, а теперь привычно домножим все это слева на какую-нибудь _m* и проинтегрируем:

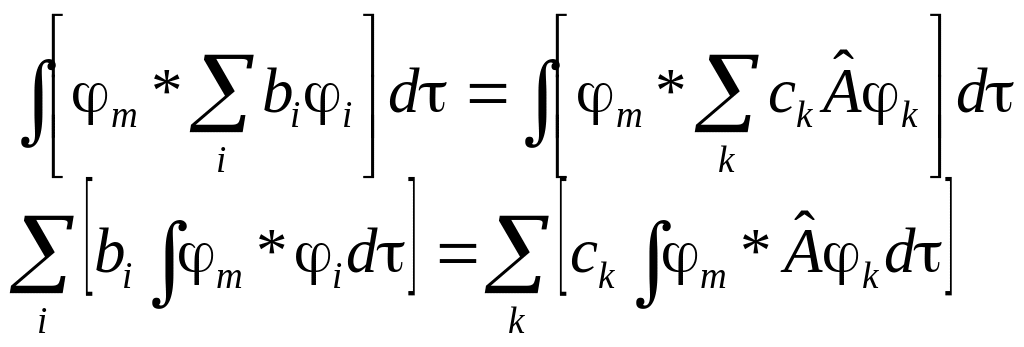
Обозначим

Обратите внимание: наши A_mk не зависят ни от каких переменных: они все уже проинтегрированы, и поэтому они – просто числа.

И теперь оставшееся выражение

описывает переход от функции  в L-представлении к функции  в L-представлении. Оказывается, этот переход можно описать набором чисел A_mk, который определяет оператор А в L-представлении.

Набор A_mk обычно записывают в виде матрицы:

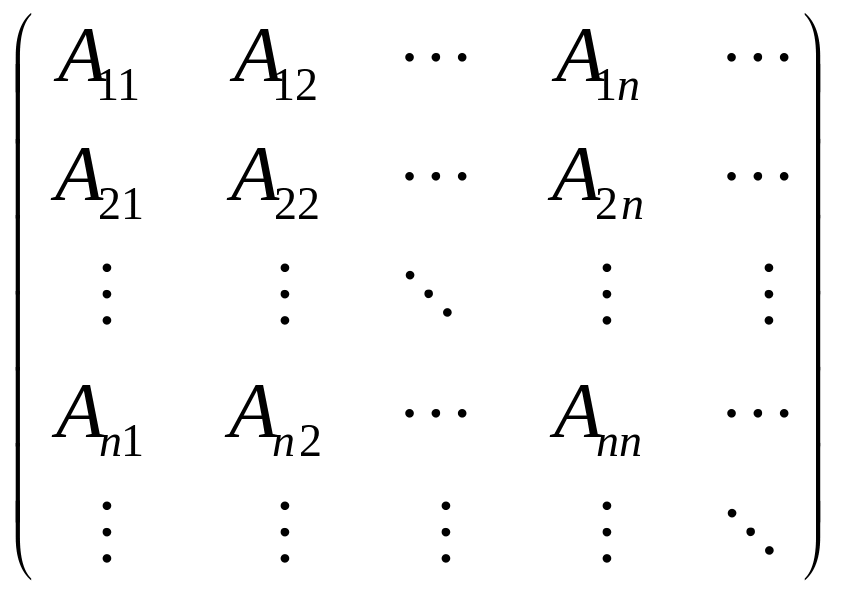
Эта матрица – всегда квадратная, число строк и число столбцов в ней равно числу базисных функций. При этом она может быть (и в общем случае обычно бывает) бесконечной. Элементы A_mk называют матричными элементами. Первый индекс нумерует строку, а второй – столбец.

9. Некоторые особые случаи

Мы рассмотрели, как выглядит произвольный оператор А в представлении другого оператора L. А как будет выглядеть оператор в своем собственном представлении? Что изменится в нашем рассмотрении?

Изменится то, что теперь функции _i будут собственными функциями оператора A, отвечающими собственным значениям а_i. Что произойдет с матричными элементами A_mk?

Рассмотрим сначала случай m  k. Все внедиагональные матричные элементы

Останутся только те элементы, для которых m = k, расположенные на главной диагонали. Матрицы такого вида называют диагональными. Чему же будут равны эти матричные элементы? Полагая базис ортонормированным, запишем:

Полученный результат (его можно даже сформулировать в виде теоремы) показывает: оператор в своем собственном представлении диагонален, причем на диагонали стоят его собственные значения.

Матрицы А и В равны, если A_kl = B_kl для всех k и l.

Матрица М* называется комплексно сопряженной М, если (M*)_kl = (M_kl)*.

Транспонированной называется матрица М^Т, для которой М^Т_kl = M_lk, т.е. такая матрица, у которой строки и столбцы меняются местами.

Пусть оператор М – эрмитов. Как будут выражаться матричные элементы матрицы М* через элементы матрицы М?

Эрмитово-сопряженной (или просто сопряженной) матрице М называют матрицу М⁺, для которой М⁺_kl = (M_lk)*. Если М⁺= М, такая матрица М называется самосопряженной или эрмитовой.

Будут ли вещественными диагональные элементы эрмитовой матрицы?

Будет ли эрмитова матрица симметричной?

Единичный оператор оставляет любую функцию неизменной. Как будет выглядеть его матрица?

15