Математический аппарат квантовой механики
1. Регулярные функции
Со школьных времен
вам знакомо понятие функции:
функция – это правило, согласно которому
всякому числу
x
(из области определения) ставится в
соответствие число
y.
Нам в нашем курсе понадобятся функции,
вообще говоря, комплексные, отвечающие
требованиям регулярности:
они должны быть конечны
во всей области определения, однозначны
и непрерывны.
Эти условия необходимы (хотя и недостаточны)
для выполнения еще одного важного
требования: эти функции должны быть
квадратично
интегрируемы,
т.е. если
– регулярная функция, а *
– ее комплексно сопряженную, то интеграл
должен
иметь конечное значение.
Если такой интеграл равен единице, функцию называют нормированной.
Пару функций, для
которых
,
называют ортогональными.
2. Операторы
При обсуждении законов квантовой механики наряду с функциями удобно ввести еще один класс математических объектов – операторы.
Оператор – это
правило, согласно которому уже каждой
функции f
ставится в соответствие другая функция
.
(обратите внимание:
операторы часто обозначают такой
«шляпкой»). Пусть, например, оператор
задает дифференцирование функции. Тогда
для функции
действие
такого оператора даст
,
т.е. наш оператор переводит функцию sin
x
в новую функцию cos
x.
Все ли понимают, что на другую функцию этот оператор будет действовать по-другому? Например, во что превратится функция u(x) = sin 2x?
Понятно, что не на всякую функцию можно подействовать оператором. Так, наш оператор дифференцирования можно применять только к дифференцируемым функциям.
Кстати, а кто-нибудь может привести пример недифференцируемой функции? Ну, например, y(x) = | x |. Заодно запомним: Не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непрерывна.
Поэтому, задавая
оператор, определяют класс функций, на
которые он действует. Говорят, что
оператор
определен
на классе
дифференцируемых функций.
Приведем еще несколько примеров.
Пусть f(x) – функция одной переменной, а оператор
.
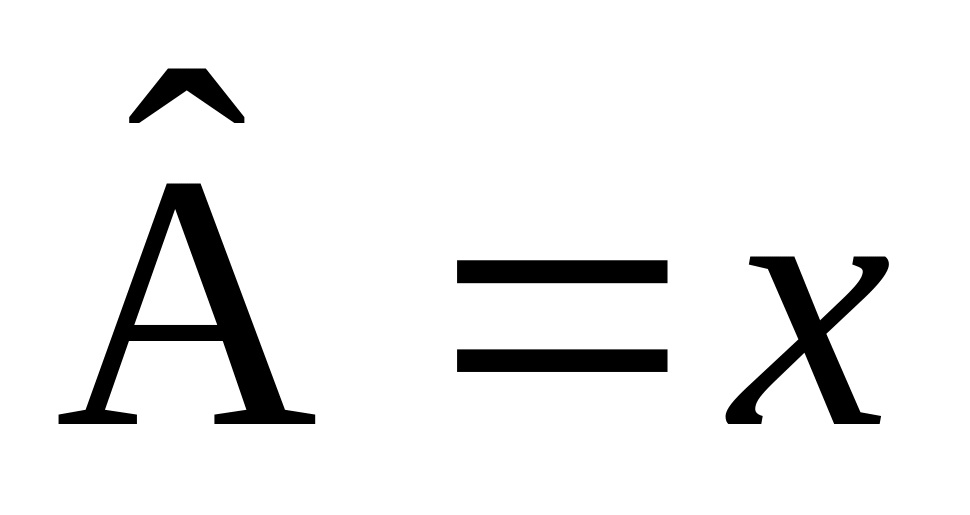Тогда
.
Действие оператора сводится к умножению
функции на аргумент.Действие оператора
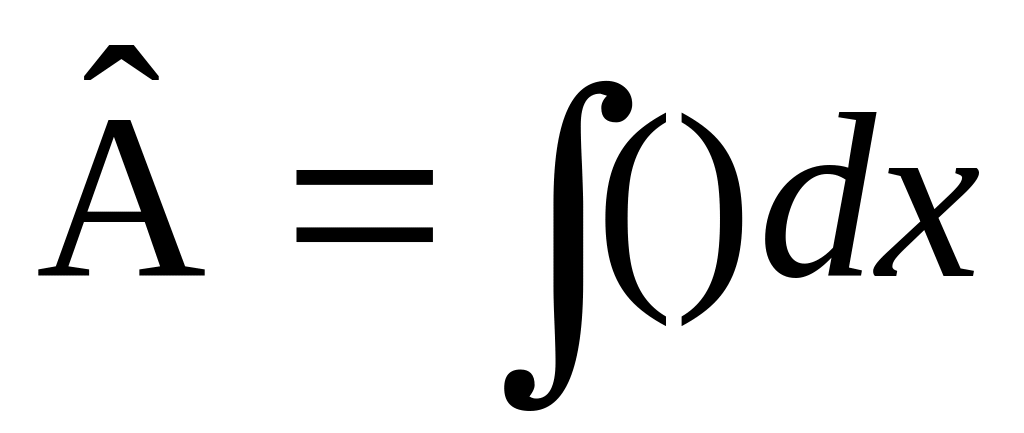приводит
к
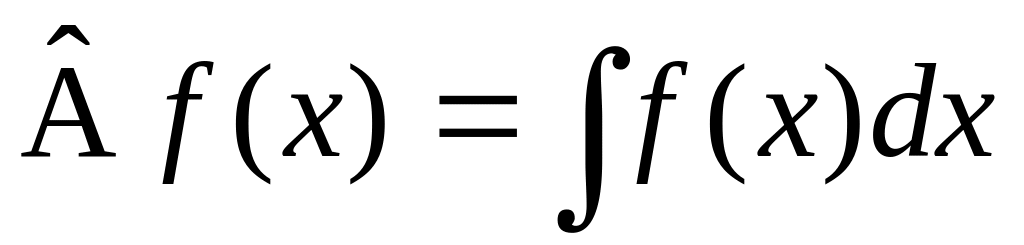.Заметим, что наша функция может быть функцией многих переменных, тогда
,
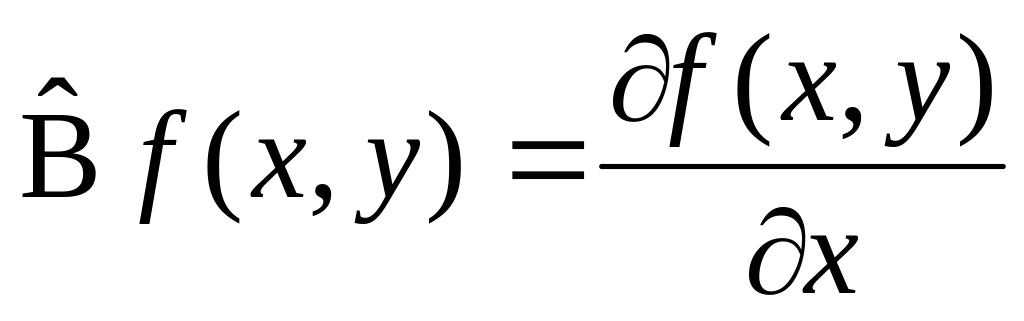оператор
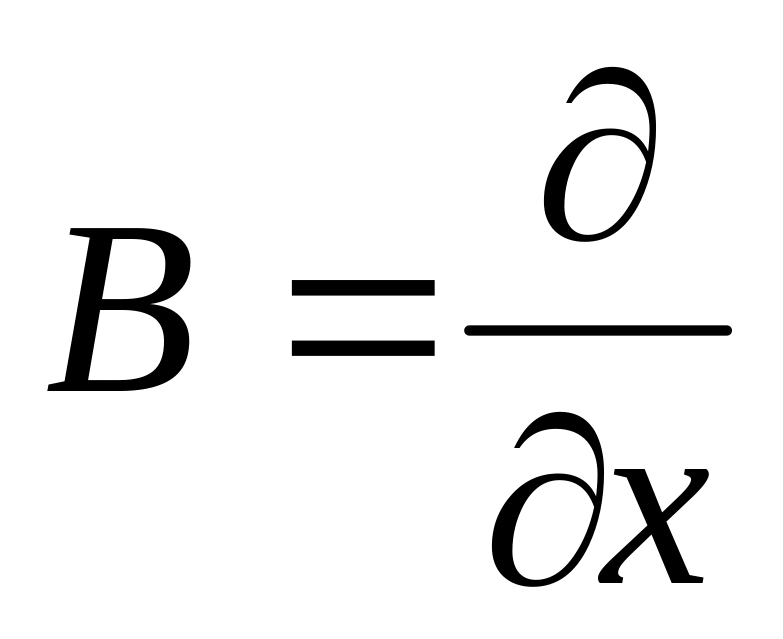задает
дифференцирование по переменной x.
Вы, наверное,
догадываетесь, что функцию можно
подвергнуть и нескольким преобразованиям.
Определим сумму
операторов как
.
Под произведением
операторов будем понимать
.
Пусть, например,
,
,
тогда
.
При этом произведение
,
т.е. умножение операторов некоммутативно.
Оператор (AB – BA), обозначаемый [A,B], называется коммутатором. Если [A,B] = 0, то говорят, что операторы коммутируют.
Найдем коммутатор
наших операторов
:
.
Таким
образом, коммутатор равен 1.
Полезно ввести
понятия единичного
оператора, такого, что для любой функции
,
и обратного
оператора А–1,
такого что А–1А
= AA–1
= I.
3. Линейные операторы.
В квантовой механике нам придется иметь дело только с линейными операторами, т.е. с такими, что
и
Эти условия можно объединить, и записать:
Легко видеть, что оператор дифференцирования линеен, а оператор возведения в квадрат – нет.