
- •1.Натуральні та цілі числа
- •Цілі числа
- •Алгебраїчні властивості
- •Ознаки подільності чисел в десятковій системі
- •2.Метод математичної індукції
- •Формулювання
- •Принцип повної математичної індукції
- •Розклад натуральних чисел на добуток простих
- •Тести простоти
- •Скільки існує простих чисел?
- •Найбільше відоме просте число
- •Деякі властивості
- •Відкриті питання
Деякі властивості
Якщо
 —
просте, і
ділить
—
просте, і
ділить
 ,
то
ділить
,
то
ділить
 або
або
 .
Цю властивість довів Евкліда, і відома
вона як лема
Евкліда. Її
використовують при доведенні основної
теореми арифметики.
.
Цю властивість довів Евкліда, і відома
вона як лема
Евкліда. Її
використовують при доведенні основної
теореми арифметики.Кільце остач
 є
полем
тоді і тільки тоді, коли
є
полем
тоді і тільки тоді, коли
 —
просте.
—
просте.Характеристика кожного поля — нуль або просте число.
Якщо — просте, — натуральне, то
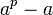 ділиться
на
(мала
теорема Ферма).
ділиться
на
(мала
теорема Ферма).Якщо
 —
скінченна група з
—
скінченна група з
 елементів,
то
містить
елемент порядку
.
елементів,
то
містить
елемент порядку
.Якщо — скінченна група, і — максимальний ступінь , який ділить
 ,
то
має
підгрупу порядку
,
яку називають підгрупою Силова, більше
того, кількість підгруп Силова дорівнює
,
то
має
підгрупу порядку
,
яку називають підгрупою Силова, більше
того, кількість підгруп Силова дорівнює
 для
деякого цілого
для
деякого цілого
 (теореми
Силова).
(теореми
Силова).Натуральне
 є
простим тоді і тільки тоді, коли
є
простим тоді і тільки тоді, коли
 ділиться
на
(теорема
Вільсона).
ділиться
на
(теорема
Вільсона).Якщо
 —
натуральне, то існує просте
,
Таке, що
—
натуральне, то існує просте
,
Таке, що
 (постулат
Бертрана).
(постулат
Бертрана).Ряд чисел, зворотних до простих, розходиться. Більш того, при

![]()
Будь-яка арифметична прогресія виду
 ,
Де
,
Де
 —
цілі взаємно-прості
числа, містить
нескінченно багато простих чисел
(Теорема
Діріхле про прості числах в арифметичній
прогресії).
—
цілі взаємно-прості
числа, містить
нескінченно багато простих чисел
(Теорема
Діріхле про прості числах в арифметичній
прогресії).Будь-яке просте число більше 3, можна представити у вигляді
 ,
або у вигляді
,
або у вигляді
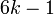 ,
де
—
деяке натуральне число.
,
де
—
деяке натуральне число.Якщо
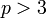 —
просте, то
—
просте, то
 кратне
24.
кратне
24.Множина додатніх значень многочлена
![]()
![]()
![]()
![]()
![]()
при невід'ємних цілих значеннях змінних збігається з множиною простих чисел.[4][5][6] Даний результат є окремим випадком доведеною Юрієм Матіясевічем діофантності будь-якої ефективно зліченної множини.
Відкриті питання
Досі існує багато відкритих запитань відносно простих чисел, найвідоміші з яких були перераховані Едмундом Ландау на П'ятому Міжнародному математичному конгресі:
Проблема Гольдбаха (перша проблема Ландау): довести або спростувати, що кожне парне число, більше двох, може бути представлено у вигляді суми двох простих чисел, а кожне непарне число, більше 5, може бути представлено у вигляді суми трьох простих чисел.
Друга проблема Ландау : чи нескінченна множина «простих близнюків» — простих чисел, різниця між якими дорівнює 2?
Гіпотеза Лежандра (третя проблема Ландау) чи вірно, що між
 і
і
 завжди
знайдеться просте число?
завжди
знайдеться просте число?Четверта проблема Ландау: чи нескінченна множина простих чисел виду
 ?
?
Відкритою проблемою є також існування нескінченної кількості простих чисел у багатьох цілочисельних послідовностях, включаючи числа Фібоначчі, числа Ферма і т. д.
Застосування
Великі прості числа (порядка
![]() )
використовують
в криптографії
з відкритим
ключем. Прості
числа також використовують в хеш-таблицях
і для генерації псевдовипадкових
чисел (зокрема,
в генераторі
псевдовипадкових чисел
Вихор
Мерсенна).
)
використовують
в криптографії
з відкритим
ключем. Прості
числа також використовують в хеш-таблицях
і для генерації псевдовипадкових
чисел (зокрема,
в генераторі
псевдовипадкових чисел
Вихор
Мерсенна).
4.Найбільший спільний дільник(НСД),найменше спільне кратне(НСК)
Найбільший спільний дільник
Найбі́льший спі́льний дільни́к (НСД) двох або більше невід'ємних цілих чисел - це найбільше натуральне число, на яке ці числа ділиться без остачі.
Позначення
Найбільший спільник дільник двох чисел a і b позначається як НСД(a, b), деколи (a, b). В англомовній літературі прийнято вживати позначення gcd(a, b).
Приклад
Число 54 може бути виражене як добуток двох інших цілих чисел кількома способами:
![]()
Отже дільники числа 54 є:
![]()
Аналонічно дільники числа 24 є:
![]()
Числа, які є у обох цих списках, є спільними дільниками чисел 54 та 24:
![]()
Найбільшим серед них є число 6. Воно найбільшим спільним дільником чисел 54 та 24. Можна записати:
![]()
Скорочення дробів
Найбільший спільний дільник використовується для скорочення дробів. Наприклад, НСД(42, 56) = 14, тому,
![]()
Властивості
НСД є комутативною функцією: НСД(a, b)= НСД(b, a).
 НСД(a, b)
НСД(a, b)

НСД(a, b, c, d) = НСД(НСД(a, b), НСД(c, d))
НСД(a, b) =|ab|/НСК(a, b), де НСК(a, b) найменше спільне кратне чисел a, b.
Обчислення НСД методом розкладу на прості множники
Нехай розклад чисел на прості множники:
![]()
![]()
Тоді
НСД![]()
Приклад
Визначимо НСД![]() .
Розклад на прості множники:
.
Розклад на прості множники:
![]()
![]() ,
,
або, подаючи для наглядності нульові степені,
![]()
![]() ,
,
Отже,
НСД![]()
Ефективним алгоритмом обчислення НСД є алгоритм Евкліда
НСД в кільці многочленів
В кільці
многочленів
![]() над
довільним полем
над
довільним полем
![]() найбільшим
спільним дільником многочленів
найбільшим
спільним дільником многочленів
![]() і
і
![]() ,
принаймі один з яких є відмінний від
нуля, називаємо нормований многочлен
найвищого степеня, який ділить обидва
многочлени
і
Обчислити
НСД можна розкладаючи
многочлен на нескоротні множники.
Можна застосувати також алгоритм
Евкліда.
,
принаймі один з яких є відмінний від
нуля, називаємо нормований многочлен
найвищого степеня, який ділить обидва
многочлени
і
Обчислити
НСД можна розкладаючи
многочлен на нескоротні множники.
Можна застосувати також алгоритм
Евкліда.
Приклад
Обчислимо НСД двох многочленів над полем дійсних чисел:
![]()
![]()
Розкладаючи многочлени на нескоротні множники
![]()
![]() ,
,
отримуємо
НСД
![]() .
.
Найменше спільне кратне
Найменше спільне кратне (НСК) двох цілих чисел a, b називаємо найменше натуральне число, яке є кратним обох цих чисел. Позначаємо НСК(a, b), в англомовній літературі LCM(a, b). Отже НСК(a, b) є найменшим натуральним числом, яке ділиться без залишку на обидва числа a, b. Означення можна – очевидним способом – узагальнити на довільну кількість аргументів.
Властивості
НСК(a, b)= НСК(b, a) (перестановка аргументів не змінює НСК).
НСК(a, b, c, d) = НСК(НСК(a, b), НСК(c, d) )
НСК(a, b) =|ab|/НСД(a, b), де НСД(a, b) найбільший спільний дільник чисел a, b.
Обчислення НСК методом розкладу на прості множники
Нехай розклад чисел на прості множники:
Тоді
НСК![]()
Приклад
Визначимо НСК . Розклад на прості множники:
,
або, подаючи для наглядності нульові степені,
,
Отже,
НСК![]()
НСК можна теж обчислити за допомогою рівності НСК(a, b) =|ab|/НСД(a, b), використавши для обчислення НСД ефективний алгоритм Евкліда
5.Ділення з остачею
Ділення з остачею (ділення по модулю, ділення націло) — арифметична операція, результатом якої є два числа: неповна частка та остача.
Визначення
Поділити з остачею ціле
число
на натуральне
число
![]() означає
представити його у вигляді:
означає
представити його у вигляді:
![]()
![]() —
називають неповною часткою,
—
називають неповною часткою,
![]() —
остачею від ділення.
—
остачею від ділення.
Якщо
![]() то:
то:
кажуть, що ділиться на
 Позначається
Позначається
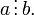
є дільником
 Визначення
дільника відрізняється від визначення
дільника
в звичайному діленні.
Визначення
дільника відрізняється від визначення
дільника
в звичайному діленні.
Наприклад, при діленні з остачею
![]() на
на
![]() отримаємо
неповну частку
отримаємо
неповну частку
![]() та
остачу
та
остачу
![]()
![]()
Також можливе ділення з остачею дійсних чисел на додатні дійсні числа.
При діленні на від'ємне число, навідь
для цілих чисел, результат не є однозначно
інтерпретуємим. В теорії чисел прийнято,
що
![]() в
мовах програмування, здебільшого, це
не виконується.
в
мовах програмування, здебільшого, це
не виконується.
