17

Федеральное агентство по образованию

Рыбинская государственная авиационная технологическая академия им. П. А. Соловьева

Кафедра «Вычислительные системы»

В. М. Комаров

Исследование резонансных свойств

параллельного колебательного контура

Лабораторная работа по дисциплине

«Основы электротехники и электроники»

Рыбинск 2008

Введение

Параллельный колебательный контур представляет собой резонансную или колебательную электрическую цепь, являющуюся неотъемлемой частью многих радиотехнических устройств. Успешное применение колебательных контуров в практике проектирования этих устройств основывается на четком представлении их свойств.

Цель работы

Целью настоящей работы является изучение резонансных свойств параллельного колебательного контура.

1. Краткие теоретические сведения

1.1. Параллельный колебательный контур и его основные характеристики

Параллельным колебательным контуром называется электрическая цепь, состоящая из двух параллельных ветвей, содержащих реактивные элементы противоположных знаков (рис. 1,а). В простейшем контуре x₁ = jL, x₂ = 1/jC, а роль активного сопротивления R₁ играет сопротивление потерь R_n реальной катушки индуктивности. В общем случае R_n = R_L + R_, где R_L – сопротивление катушки индуктивности постоянному току, а R_ – сопротивление потерь, вносимое сердечником катушки на рабочей частоте. При этом активным сопротивлением R₂, учитывающим потери в реальном конденсаторе, чаще всего можно пренебречь. Схема простейшего колебательного контура, построенная в соответствии с этим, приведена на рис. 1,б.

Важнейшими характеристиками контура являются его волновое или характеристическое сопротивление и добротность .

Параллельному колебательному контуру свойственно явление, называемое резонансом токов. Резонанс токов наступает на частоте ₀ гармонического сигнала, на которой реактивная проводимость контура b = 0.

Полная комплексная проводимость контура Y = q – jb есть сумма комплексных реактивных проводимостей его ветвей, т. е. Y = Y_L + Y_C.

а) б)

Рис. 1. Параллельный колебательный контур а) схема в общем виде; б) простейший параллельный контур

Комплексная проводимость ветви с индуктивностью

.

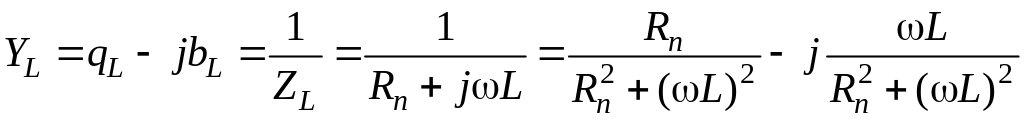Отсюда,

.

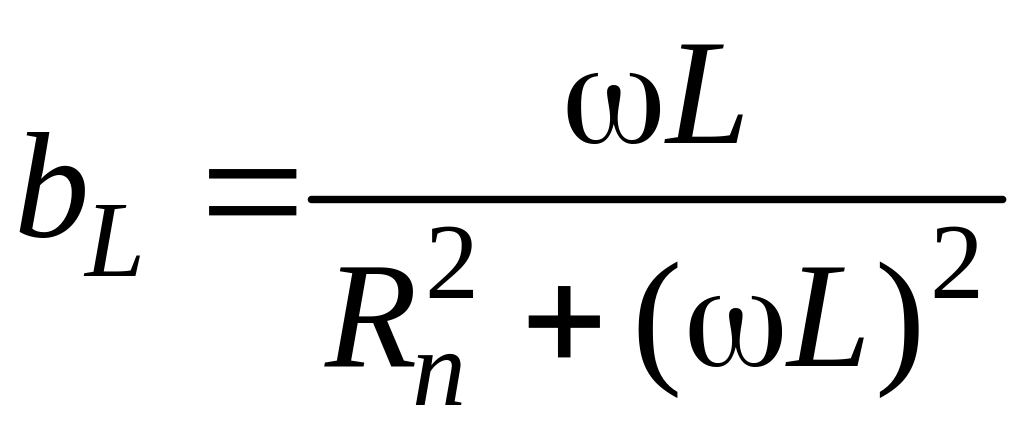Комплексная проводимость ветви с емкостью

.

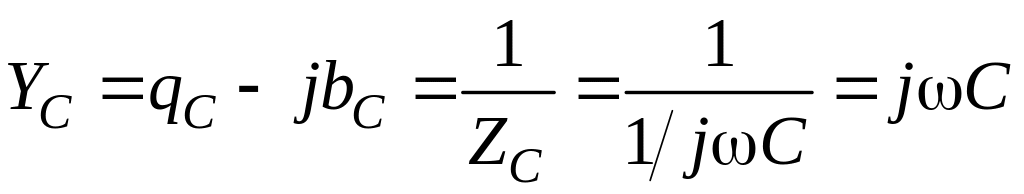Отсюда,

b_C = – C.

Таким образом, полная комплексная проводимость простейшего контура

.

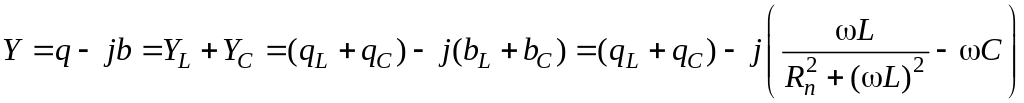Резонансная частота ₀ параллельного колебательного контура определяется из условия

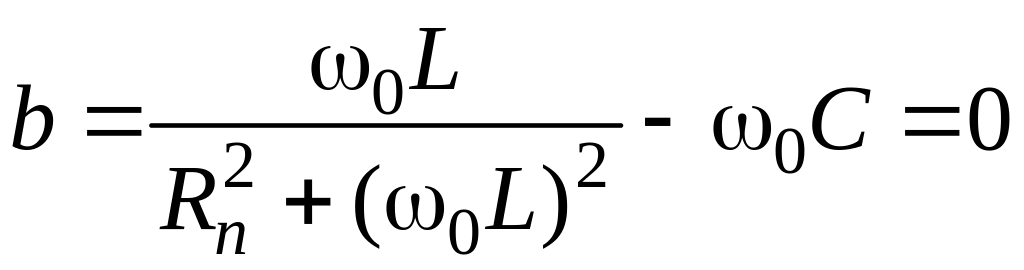
После простейших преобразований можно получить

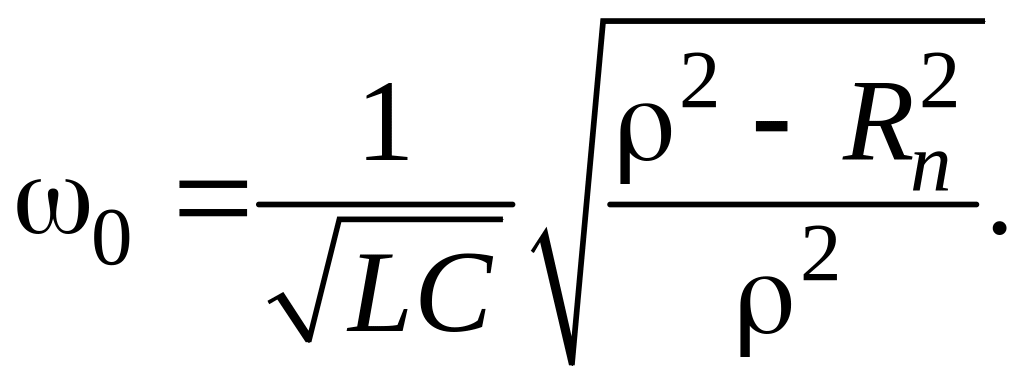
В практически используемых контурах R_n   и

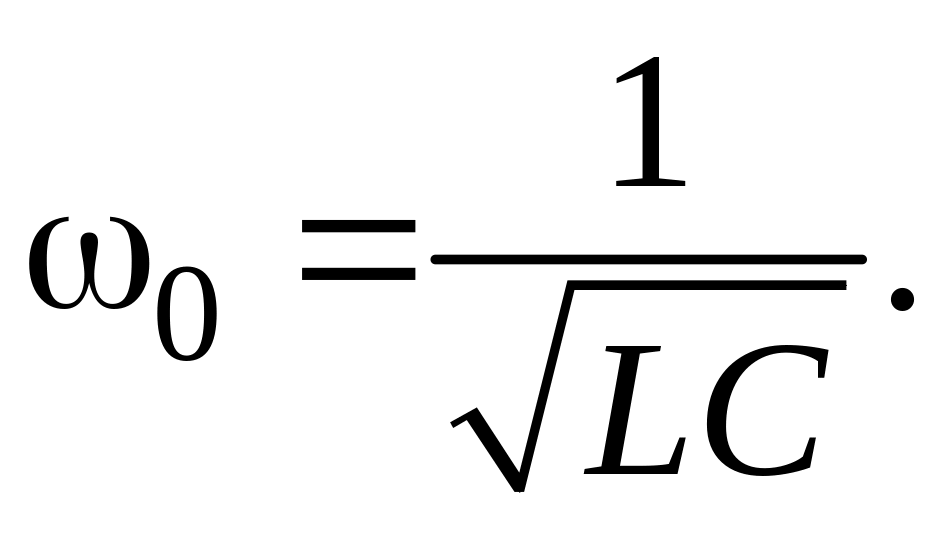
Отсюда следует, что

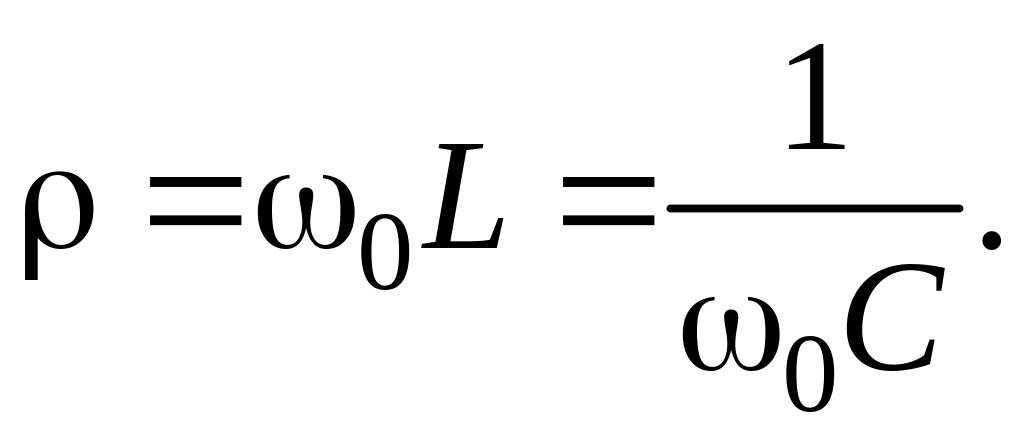
1.2. Резонансные кривые параллельного колебательного контура

Резонансной кривой параллельного колебательного контура называется зависимость напряжения на контуре от частоты U_mк().

Безразмерной резонансной кривой называется зависимость, определяемая отношением,

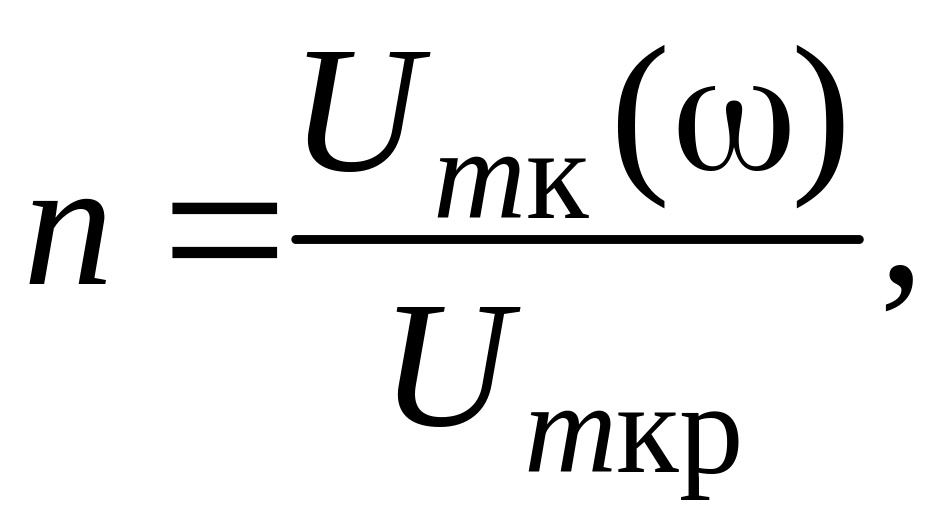
где U_mкр – напряжение на контуре при резонансе.

При питании параллельного колебательного контура от идеального источника гармонического тока (рис. 2) можно записать

(1)

(2)

где – ток идеального источника гармонического тока;

Z_э – эквивалентное сопротивление контура на частотах, не равных резонансной;

Z_эр – эквивалентное сопротивление контура на резонансной частоте.

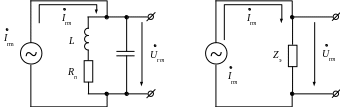
а) б)

Рис. 2. Включение параллельного колебательного контура в электрическую цепь а) схема с идеальным источником гармонического тока; б) эквивалентная схема включения

С учетом этого, уравнение безразмерной резонансной кривой приобретает вид

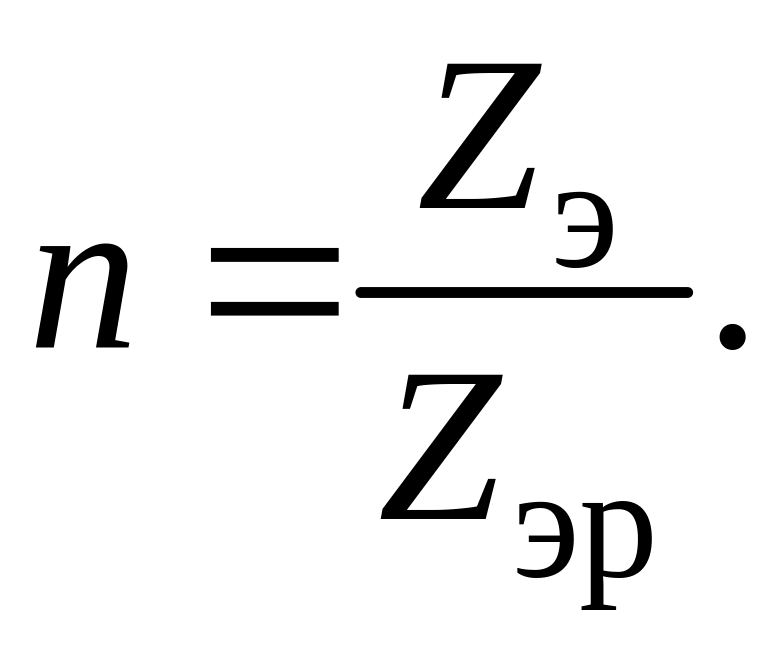
Эквивалентное сопротивление контура

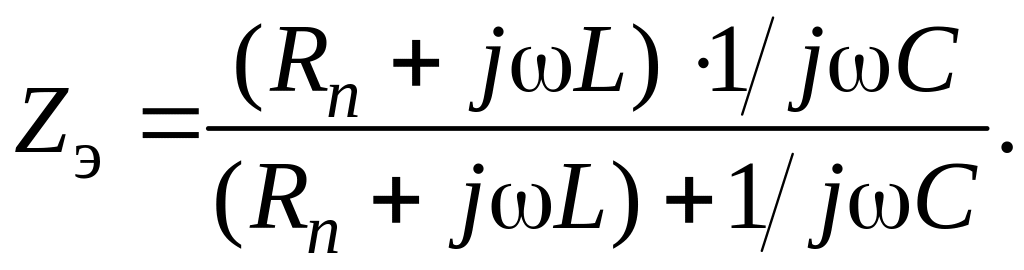
В практически используемых контурах на частотах, близких к резонансной, R_n  L. Отсюда,

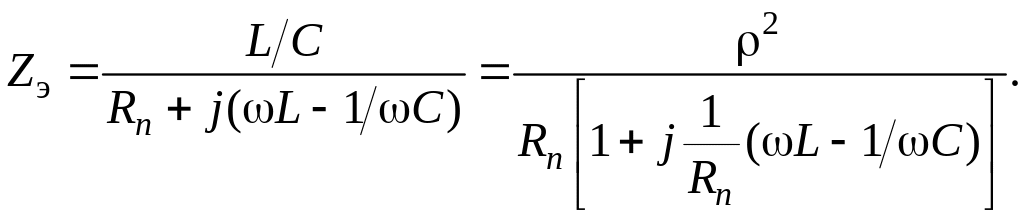(3)

Рассмотрим выражение

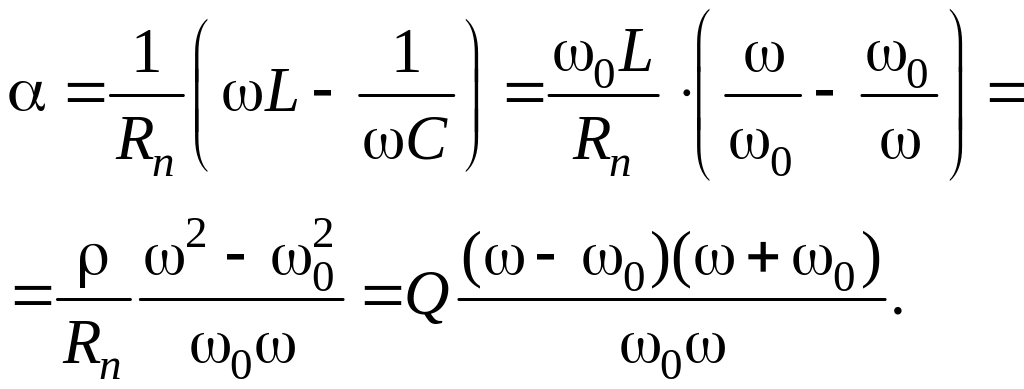
На частотах, близких к резонансной,  – ₀ = Δ,  + ₀ = 2.

Отсюда,

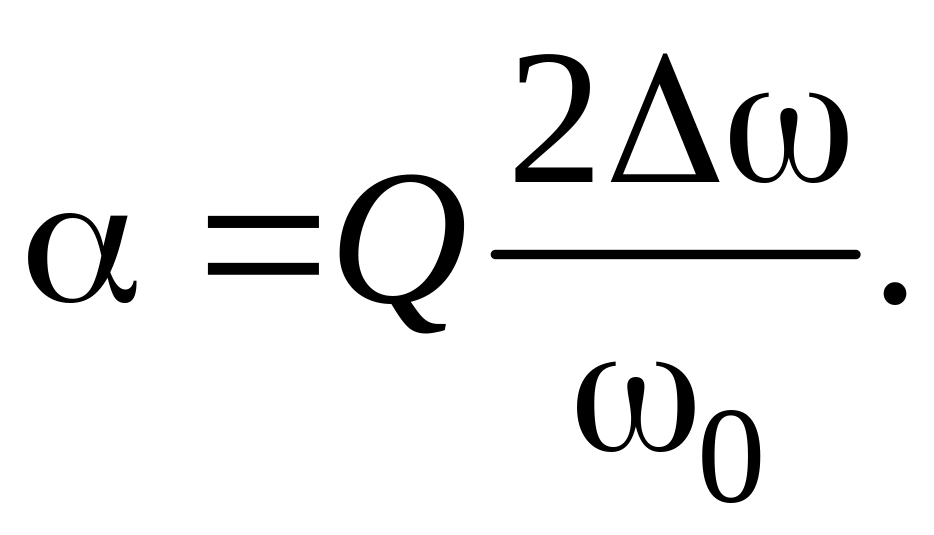(4)

Величина α называется обобщенной расстройкой колебательного контура. Подставляя α в выражение (3), можно получить

Модуль эквивалентного комплексного сопротивления контура

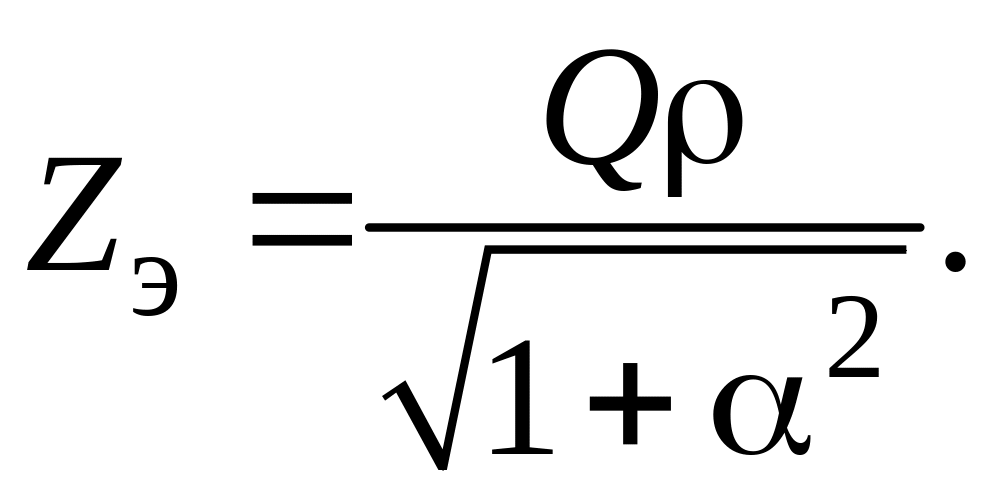
На резонансной частоте α =0 и Z_эр = Qρ. Следовательно,

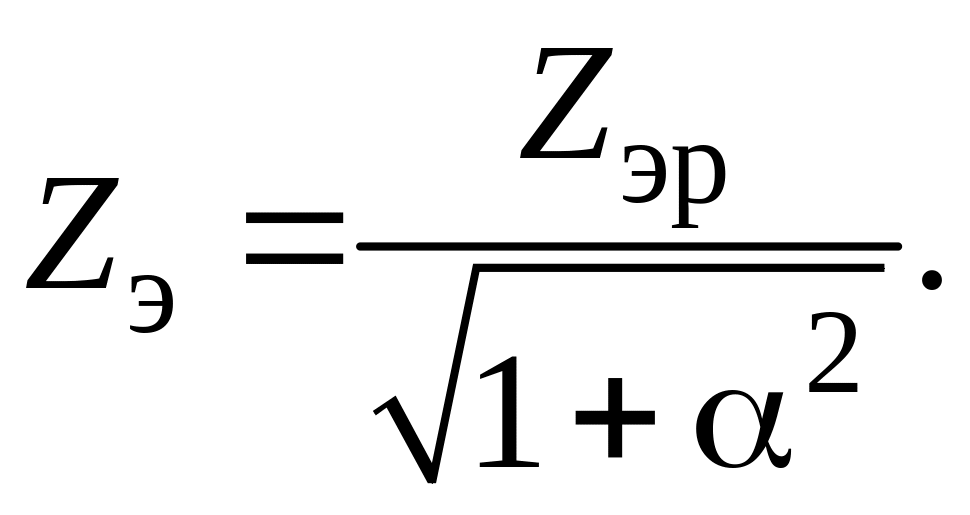(5)

Таким образом, уравнение безразмерной резонансной кривой имеет вид

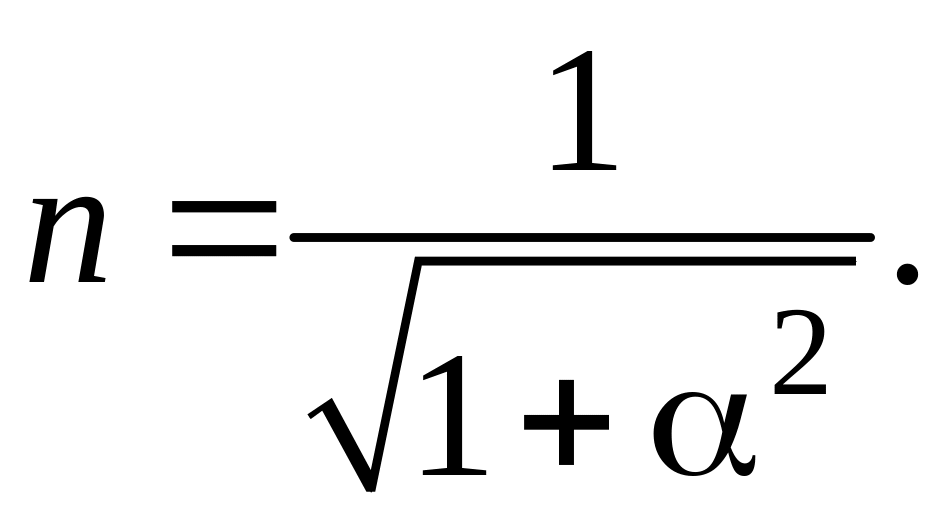(6)

Фазовую характеристику параллельного контура можно найти из выражения

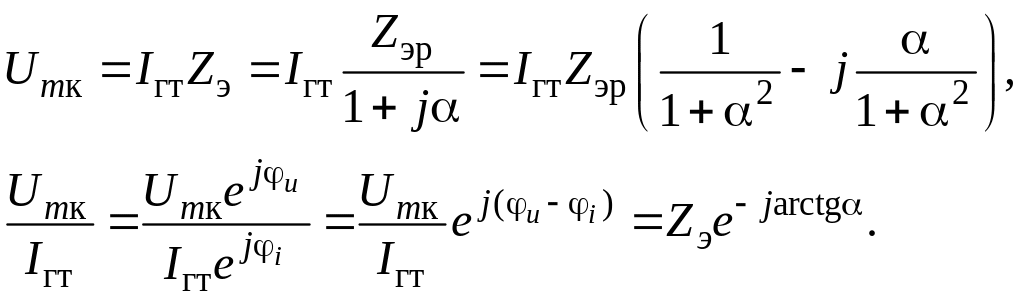
Отсюда, фазовая характеристика контура

φ = ψ_u – ψ_i = –arctgα, (7)

где ψ_u – начальная фаза напряжения;

ψ_i – начальная фаза тока.

Г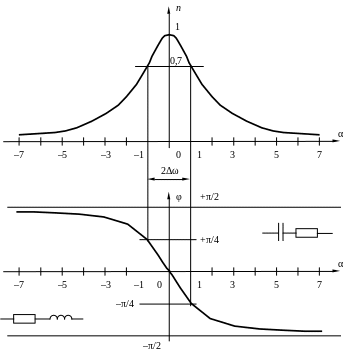 рафики n(α) и φ(α), построение по формулам (6) и (7), приведены на рис. 3.

а)

б)

Рис. 3. Резонансные кривые параллельного колебательного контура а) безразмерная резонансная кривая; б) фазовая характеристика

Из графика безразмерной резонансной кривой n(α) следует, что параллельный колебательный контур обладает свойством избирательности некоторой полосы частот, называемой полосой пропускания контура. Полосой пропускания является полоса частот, в которой n  [0,7;1] (см. рис. 3,а).

Из графика фазовой кривой φ(α) следует, что при α  0 (  ₀) α  0, т. е. напряжение на контуре опережает ток в неразветвленной цепи и контур носит индуктивный характер; при α   ( > ₀) φ < 0, т. е. напряжение на контуре отстает от тока и контур носит емкостный характер.

Уравнение резонансной кривой U_тк() может быть легко получено из (1) с учетом (5) и (4)

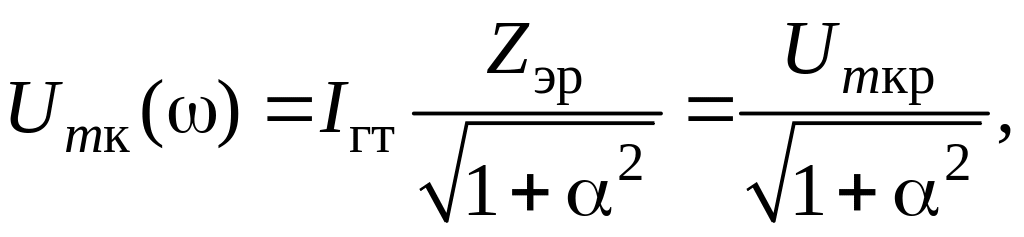(8)

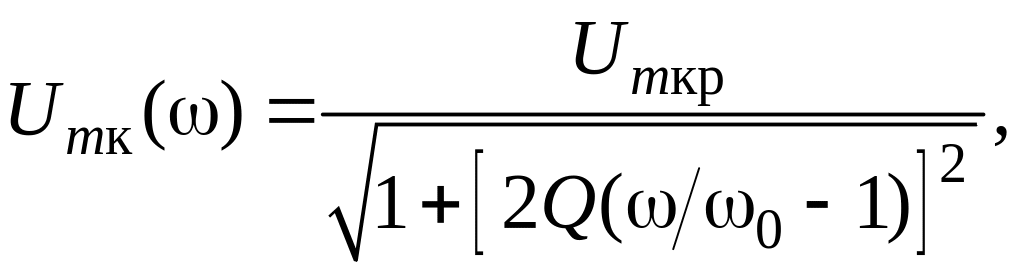
где

U_mкр = I_гтZ_эр = I_гтQρ

Аналогичным образом, подставляя значение α в формулы (6) и (7), можно получить зависимость от частоты безразмерного резонансного коэффициента n() и фазовой характеристики φ()

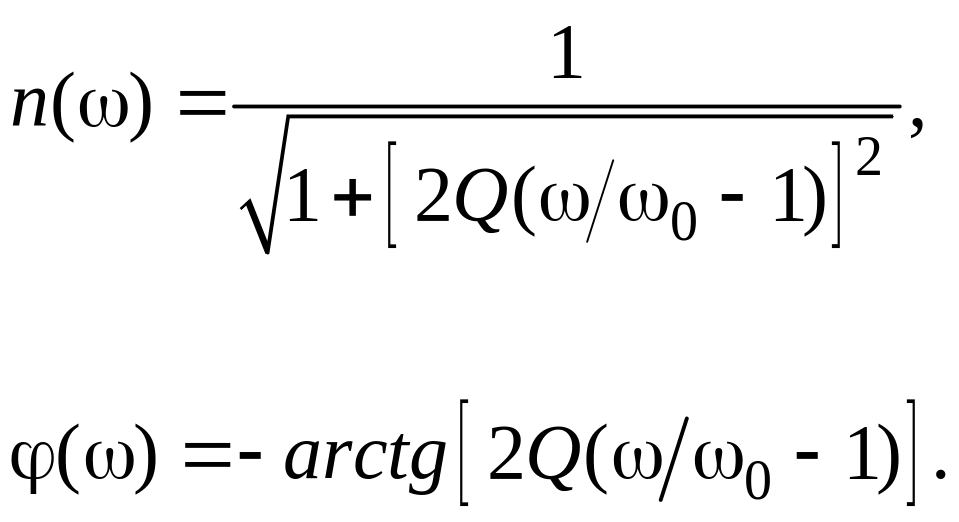
На границах полосы пропускания , U_тк() = 0,7U_ткр и из (6), (8) очевидно, что при этом α = ± 1.

Исходя из этого, легко найти значение реальной добротности Q_р колебательного контура по экспериментально полученным зависимостям U_тк() или n(). Действительно, определив по экспериментальной кривой значения полосы пропускания 2Δ и резонансной частоты ₀ контура, в соответствии с (4) можно получить

Учитывая, что = 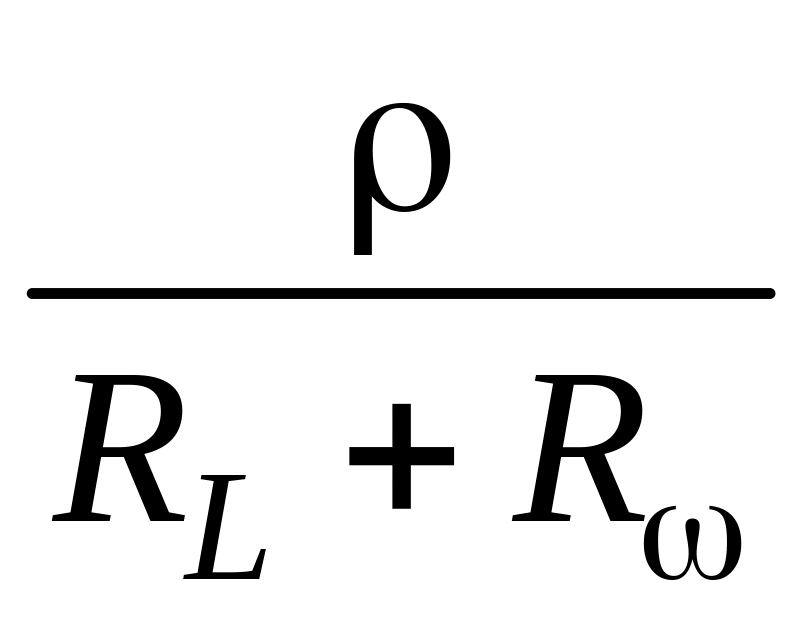, по найденному значению добротности и известным значениям ρ и R_L не представляет труда определить величину сопротивления потерь R_, вносимого сердечником катушки индуктивности на резонансной частоте

Для отыскания физического смысла добротности параллельного колебательного контура найдем отношение тока в контуре при резонансе к току в неразветвленной части цепи .

Ток в неразветвленной части цепи при питании контура от идеального источника гармонического тока (см. рис. 2,а) равен .

Определим значения токов в ветвях контура при резонансе, учитывая, что R_n  ₀L,

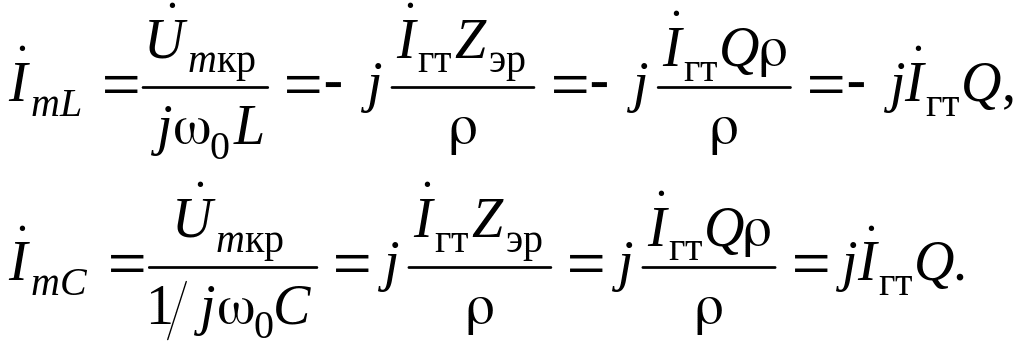
Отсюда следует, что токи в ветвях контура при резонансе равны по величине и противоположны по фазе, что позволяет рассматривать их как единый контурный ток , последовательно обтекающий все элементы контура.

Таким образом,

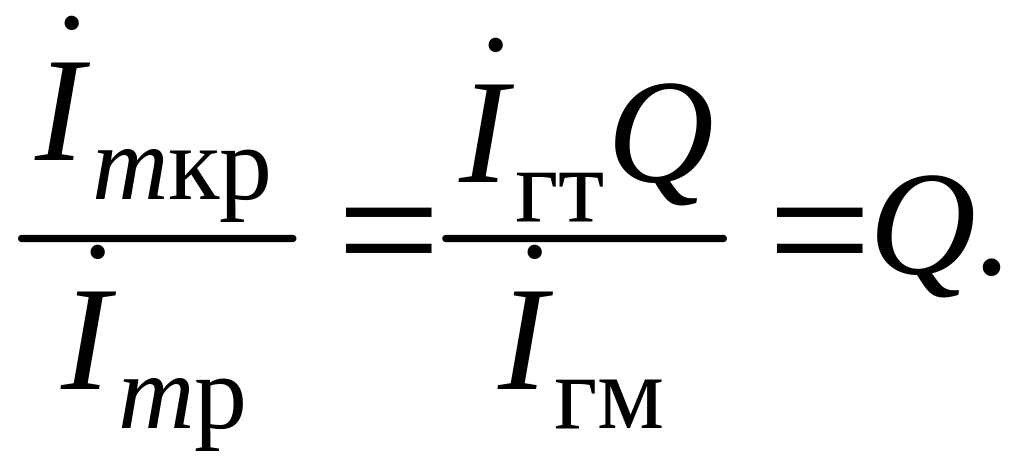
Добротность параллельного колебательного контура показывает во сколько раз ток в контуре при резонансе больше тока в неразветвленной части цепи.

В идеальном контуре R_n = 0 и Q → ∞. Следовательно, ток в идеальном параллельном контуре при резонансе I_mкр → ∞.