6. Определение устойчивости, управляемости и наблюдаемости исследуемой сау.

1. Определение устойчивости исследуемой системы.

Устойчивость характеризует свойство системы возвращаться в исходное состояние равновесия или вынужденного движения после снятия внешнего воздействия на систему. Устойчивость является обязательным условием работоспособности систем регулирования, проверяемым в первую очередь при их анализе и синтезе.

На основе методов, разработанных А.М.Ляпуновым, можно утверждать, что линейная стационарная динамическая система устойчива, если:

1. все собственные числа матрицы А имеют отрицательные значения;

2. все собственные числа с нулевыми вещественными частями (если таковые имеются) являются некратными корнями.

Сформулируем математический признак устойчиво­сти: для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицатель­ную действительную часть. Другими словами – чтобы все полюса системы были левыми. Корни полинома числителя передаточной функции (нули функции) на устойчивость системы не влияют.

Таким образом, чтобы определить устойчивость исследуемой системы, необходимо найти корни характеристического полинома. Для этого используем систему MatLab:

» p = [0.000000078 0.00009555 0.01843 1.008 131.9 1667 1440];

» r = roots(p)

r =

1.0e+002 *

- 999.96

- 207.22

- 2.06 + 0.86.54i

- 2.06 - 0.86.54i

- 12.75

Так как все корни характеристического полинома имеют отрицатель­ную действительную часть, исследуемая система устойчива.

2. Определение управляемости исследуемой системы.

Управляемость характеризует принципиальную возможность изменения состояния системы с помощью внешних воздействий.

Для проверки управляемости и наблюдаемости динамической системы существуют аналитические критерии, разработанные Р.Калманом.

Для того, чтобы динамическая система была полностью управляемой необходимо и достаточно, чтобы матрица управляемости системы

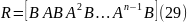
имела ранг равный .

Найдем матрицу управляемости исследуемой системы и определим ее ранг в системе MathCad:

Рис. 7. Определение управляемости исследуемой системы.

Ранг матрицы управляемости равен пяти, а порядок системы , то есть:

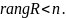
Используя граф системы для жордановой канонической формы (рис.6.) и ранг системы можно сделать следующий вывод: исследуемая система является частично управляемой.

3. Определение наблюдаемости исследуемой системы.

Наблюдаемость характеризует принципиальную возможность определения состояния системы по наблюдениям за ее выходными сигналами.

Для того, чтобы динамическая система была полностью наблюдаемой необходимо и достаточно, чтобы матрица наблюдаемости системы

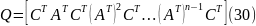
имела ранг равный .

Найдем матрицу наблюдаемости исследуемой системы и определим ее ранг в системе MathCad:

Рис. 8. Определение наблюдаемости исследуемой системы.

Так как ранг матрицы наблюдаемости равен порядку системы, исследуемая система является полностью наблюдаемой.

К такому же выводу приводит граф системы, который был построен при рассмотрении жордановой канонической формы (рис.6.).