Литература

1. Бартоломей Г.Г., Бать Г.А. и др. Основы теории и методы расчета ядерных энергетических реакторов: Учебное пособие для вузов. – М.: Энергоатомиздат, 1989.

2. Герасимов В.В., Монахов А.С. Материалы ядерной техники. – М.: Атомиздат, 1973.

3. Смиренский О.В. Физика и расчет ядерных реакторов: Учебное пособие.– Томск: Изд-во ТПУ, 1997.

Контрольные вопросы и задания

1. Нейтронные потоки в реакторах без отражателя.

2. Влияние отражателя на распределения нейтронных потоков в ядерном реакторе.

3. Почему в центре активной зоны ядерного реактора без отражателя плотность потока нейтронов выше, чем на периферии?

4. Определение и физический смысл коэффициента неравномерности.

5. Коэффициенты неравномерности потоков нейтронов реакторов различной формы.

6. Основные способы выравнивания нейтронных потоков в ядерном реакторе.

7. Физические принципы "работы" отражателя.

8. Гомогенный ядерный реактор с отражателем в одногрупповом и двухгрупповом приближениях.

9. В каком ядерном реакторе, с отражателем или без него, критические размеры меньше и почему?

10. Поставить задачу о гомогенном ядерном реакторе с отражателем в одногрупповом приближении (математическая и физическая постановка).

11. Определение понятия "эффективная добавка за счет отражателя", ее единицы измерения.

12. От чего зависит величина эффективной добавки за счет отражателя для толстых и тонких отражателей.

13. Почему аналитические решения не могут быть получены для ядерного реактора, окруженного со всех сторон отражателем?

14.Чем объясняется всплеск в распределении потока тепловых нейтронов в отражателе?

15. На каком расстоянии от активной зоны он примерно расположен?

16. Основные принципы расчета ядерного реактора, окруженного со всех сторон отражателем.

17. Условие критичности гомогенного ядерного реактора с отражателем в форме бесконечной пластины в одногрупповом приближении.

18. Условие критичности гомогенного ядерного реактора с отражателем в форме сферы в одногрупповом приближении.

19. Условие критичности гомогенного цилиндрического ядерного реактора с боковым отражателем в одногрупповом приближении.

20. Условие критичности гомогенного цилиндрического ядерного реактора с торцевым отражателем в одногрупповом приближении.

21. Условие критичности гомогенного ядерного реактора в форме параллелепипеда с боковым отражателем в одногрупповом приближении.

Метод Экспоненциальной призмы

Цель работы: изучение метода экспоненциальной призмы как одного из методов экспериментального определения критических параметров ядерных реакторов; определение нейтронно-физических характеристик слабопоглощающих сред

Теоретические основы

Для стационарного случая уравнение диффузии имеет вид:

, (1)

где Ф(r) – плотность потока нейтронов; D – коэффициент диффузии; – макроскопическое сечение поглощения нейтронов в среде; S(r) – функция, описывающая распределение потока нейтронов источника.

В общем случае при наличие делящихся ядер в системе процесс деления увеличивает число нейтронов в раз за 1 с в 1 см³ за каждый акт деления. При этом в процессе деления рождаются быстрые нейтроны, которые в результате замедления становятся тепловыми. Тогда функция источника тепловых нейтронов имеет следующий вид:

, (2)

где – вероятность того, что быстрый нейтрон, рожденный в точке замедлится до теплового в точке r. Интегрирование ведется по всему объему системы – V.

Если пренебречь поглощением нейтронов в процессе замедления, то вдали от источника существует область, в которой устанавливается единый для всех точек Максвелловский спектр тепловых нейтронов. Для этой области выражение (1) с учетом (2) принимает следующий вид:

. (3)

Преобразуя выражение (3), получаем:

. (4)

В случае, когда в среде отсутствует размножение нейтронов ( =0), зная, что (L – длина диффузии), уравнение (4) имеет следующий вид:

. (5)

Если положить , где параметр является материальным параметром размножающей системы, и положить , то уравнения (4) и (5) приобретут одинаковый вид. В этом смысле параметр является аналогом материального параметра размножающей системы.

Реальные ядерные реакторы характеризуются большой сложностью взаимосвязанных нейтронно-физических, теплофизических, теплогидравлических и др. процессов. Поэтому экспериментальное определение его параметров крайне затруднено. В связи с этим на стадии разработки реакторов используют ряд экспериментальных методов, позволяющих определять те или иные характеристики реакторов. Одним из таких является метод экспоненциальной призмы.

Под призмой подразумевается прямоугольный параллелепипед подкритических размеров. Для определения характеристик проектируемого реактора призму изготавливают таким образом, что внутренняя геометрия призмы и ее материальный состав соответствуют таким же характеристикам активной зоны проектируемого реактора.

Рассмотрим реализацию метода призмы на примере неразмножающей системы, поэтому воспользуемся исходным уравнением (5). В декартовой системе координат уравнение (5) [а при наличии делящихся материалов уравнение (4)] имеет вид:

. (6)

Пусть в уравнении (6) переменные разделяются следующим образом:

. (7)

Подставляя выражение (7) в (6) получаем:

. (8)

Каждое слагаемое из левой части уравнения (8) зависит только от одной переменной, причем эти переменные взаимно независимые. Поскольку тем не менее сумма этих слагаемых равна постоянной, то каждое из них должно быть равно также постоянной. Таким образом, уравнение (8) трансформируется в систему следующего вида:

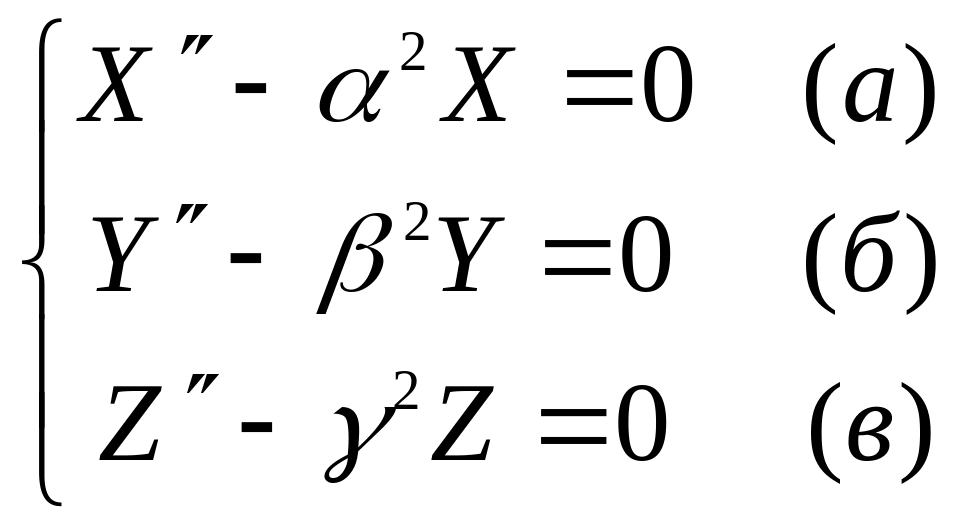, (9)

где , , – произвольные постоянные, причем:

. (10)

Решения системы (9) известны:

. (11)

При этом постоянные , , могут быть как действительными, так и мнимыми числами. Если, например, – мнимое число, т.е. , то уравнение (9а) примет вид: , а его общее решение записывается следующим образом:

. (12)

С другой стороны, если, например, постоянная – действительное число, т.е. , то уравнение (9в) имеет следующее общее решение:

. (13)

Так как дифференциальные уравнения линейны, то общие решения допускают суперпозицию. Поэтому представим общее решение уравнения (6) в следующем виде:

. (14)

Тогда условие (10), при котором выражения (9) действительно являются решениями уравнения (6), в данном случае преобразуется к виду:

(15)

Н

Рис. 1 Схема прямоугольной призмы.

а рис.1 приведена схема прямоугольной призмы в декартовой системе координат. Размеры a, b, c – экстраполированные размеры призмы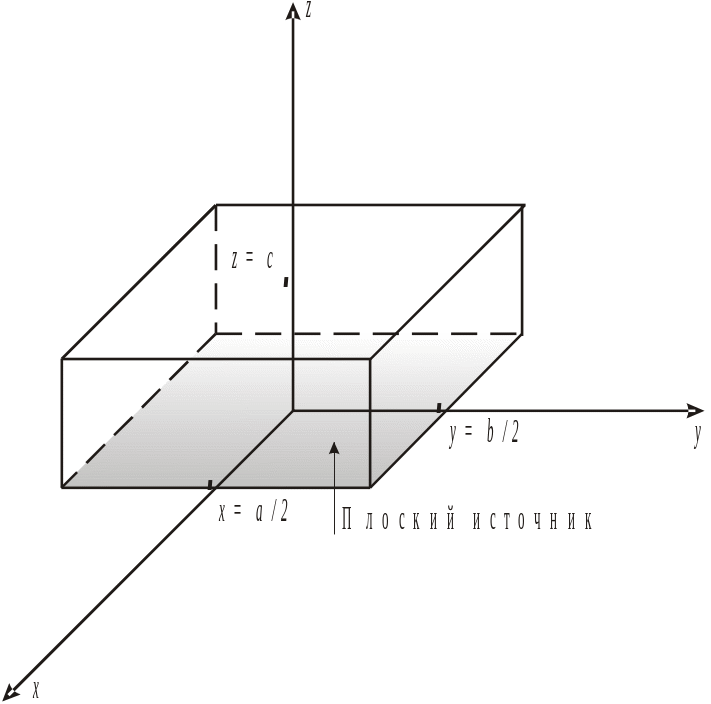: ; ; , где , , – реальные размеры призмы, d – длина экстраполяции. Предположим, что на нижнем торце призмы (на плоскости z=0) помещен источник тепловых нейтронов. В качестве источника, например, могут выступать замедлившиеся нейтроны от лабораторного нейтронного источника, причем источник должен быть расположен быть в замедлителе на некотором расстоянии (не менее 3 ) от основания сборки (z=0), чтобы нейтроны, входящие в сборку, были тепловыми. В этом случае граничные условия для уравнения (6) записываются в следующем виде:

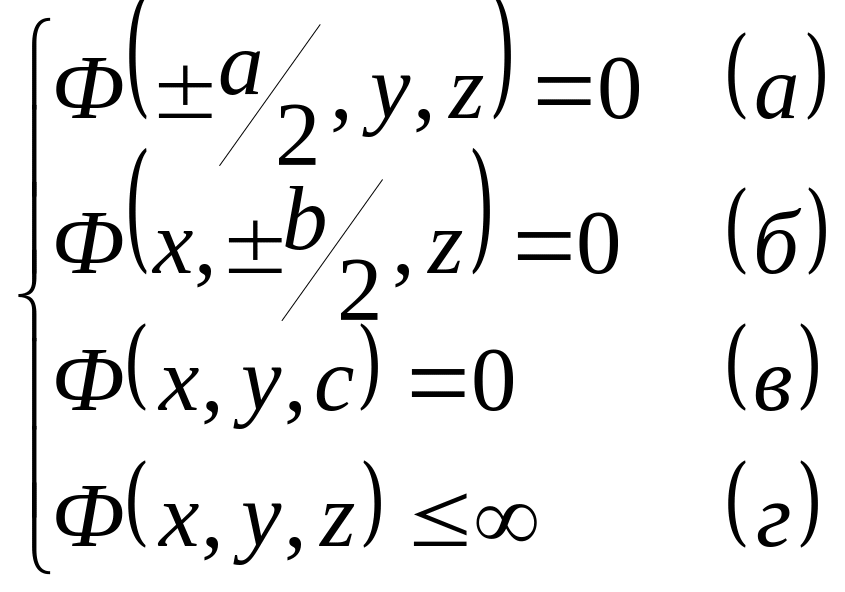. (16)

Ввиду условия (16а) из решения (14) следует, что:

,

т.е. решения X(x) симметричны относительно начала координат и на границах обращается в нуль. Это возможно, если постоянная – мнимое число, так как экспонента с действительным показателем нигде в нуль не обращается. При этом отсюда же следует, что число n должно быть положительным . Поэтому для функции X_n(x) необходимо использовать решение типа (12). Причем вследствие установленной симметрии функции X_n(x) постоянная должна обращаться в нуль:

где . (17)

По аналогии можно записать решение для функции Y_m(y):

где . (18)

При этом условие (15), при котором выражения (17) и (18) являются решением уравнения (6), примет вид:

,

отсюда, обозначив , имеем:

. (19)

Из условия (19) следует, что постоянная является действительным и положительным числом.

Значения , , , определяемые из условия (19), при которых решение (14) верно называются собственными значениями, т.е. только при определенных значениях указанных постоянных уравнение (6) имеет решение. Причем из (19) следует, что – наименьшее собственное значение постоянной .

Таким образом, решение для функции Z_k(z) применимо решение типа (13):

. (20)

Используя граничное условие (16в) можно записать:

.

Расписывая гиперболические функции в соотношении (20) по определению через экспоненты, записываем общее решение уравнения (6):

, (21)

где , Постоянная B_mn определяется мощностью реального источника нейтронов.

Из физических соображений ясно, что слагающие (гармоники) плотности потока нейтронов затухают при удалении от источника. Медленнее всего затухает первая гармоника с m=1 и n=1, обладающая наименьшим показателем экспоненты. Другими словами существует область , где все гармоники, кроме первой, практически не будут вносить вклад в плотность потока нейтронов. Тогда для этой области решение (21) принимает следующий вид:

.

Рассматривая только зависимость по координате z в конечном итоге получаем:

, (22)

где .

Анализируя выражение (22) видим, что множитель характеризует влияние, оказываемое утечкой нейтронов через верхний торец призмы. Если рассматривать распределение потока в точках, не слишком близких к дальнему концу призмы (z=c), то второе слагаемое в квадратных скобках мало, т.е. существует расстояние , на котором влияние торца призмы пренебрежимо мало. Таким образом, для области характер зависимости Ф(z) имеет экспоненциальный вид:

. (23)

Пусть экспоненциальный участок зависимости Ф(z) известен. Тогда экспериментальное определение постоянной сводится к измерению плотности потока нейтронов в двух точках этого участка. Предположим, что такие измерения были проведены и получены следующие результаты: в точке z₁ плотность потока нейтронов составляет величину Ф₁, а в точке z₂ – Ф₂. Запишем выражение (23) для каждого результата:

.

Логарифмируя оба результата, получаем:

.

Из второго соотношения выразим lnB и подставим в первое. В итоге окончательно получим:

. (24)

Определив постоянную можно, зная размеры призмы, рассчитать параметр , используя условие (19):

. (25)

Таким образом, метод призмы позволяет определить параметр , который в случае размножающей среды представляет собой материальный параметр, т.е. ядерный реактор, построенный из тех же материалов, будет иметь такой же материальный параметр. В критическом реакторе материальный параметр равен геометрическому. Зная же геометрический параметр, можно рассчитать критические размеры проектируемого реактора. Такой же эксперимент для неразмножающей среды позволяет измерить длину диффузии нейтронов в ней.