1. Числовые ряды: определение числового ряда, его суммы, сходящиеся и расходящиеся ряды. Свойство сход-ся рядов. Необходимый признак сходимости.

Пусть задана бесконечная последовательность, то есть бесконечное перенумерованное множество действительных чисел:

U₁, U₂, U₃, …, U_n, U_n+1, …

U₁ + U₂ + U₃ + … + U_n + … = ^∞∑ _n=1 U_n - называется рядом

!(здесь и далее ∞ пишется над ∑, а n=1 под ∑ - прим.)!

Ряд ^∞∑ _n=1U_n называют конечным, если начиная с некоторого числа n все его члены = 0. В противном случае – ряд бесконечен.

Пусть дан ряд ^∞∑ _n=1Un => S₁ = U₁; S₂ = U₁ + U₂; S₃ = U₁+ U₂ + U₃;

S _n = U₁ + U₂ + … + U _n =>

Сумма S _n – n-ая частичная сумма ряда

Если (n->∞)lim S _n = S говорят, что ряд сходится и имеет сумму, в противном случае ряд расходится и суммы не имеет. !(n->∞ - пишется под lim – прим.)!

S ≈ S _n => R _n = S – S _n “R _n” – остаток ряда

│R _n│ - показывает погрешность допустимую при замене S на S _n

а) произведение сходящегося ряда Un на число С ≠ 0 есть ряд сходящийся, причем если ^∞∑ _n=1U_n = U, то сумма ряда C ∙ ^∞∑ _n=1U_n = ^∞∑ _n=1 C ∙ U_n = C ∙ U

б) сумма (разность) двух сходящихся рядов есть ряд сходящийся, причем если (n->∞)lim S _n = S, а (n->∞)lim δ _n = δ => (n->∞)lim ( S _n ± δ _n ) = U ± V

Док-во:

^∞∑ _n=1 U_n = U₁ + U₂ + U₃ + … + U_n + … =>

S _n = U₁ + U₂ + U₃ + … + U_n

δ _n = C∙U₁ + C∙U₂ + C∙U₃ + … + C∙U_n = C∙S _n =>

^∞∑ _n=1 C ∙ U_n = C∙U₁ + C∙U₂ + C∙U₃ + … + C∙U_n + ... =>

(n->∞)lim δ _n = C∙S ; (n->∞)lim S _n = S

Теорема:

Если ряд ^∞∑ _n=1 U_n сходится, то его общий член стремится к 0, при n->∞ (n->∞)lim U _n = 0

Док-во:

^∞∑ _n=1 U_n - сходящийся => S _n = U₁ + U₂ + U₃ + … + U_n => (n->∞)lim S _n = S

S _{n - 1} = U₁ + U₂ + U₃ + … + U_{n - 1} => (n->∞)lim S _{n - 1} = S =>

(n->∞)lim S _n = (n->∞)lim(S _{n – 1} + U _n) = S + U _n => U _n = 0

2. Знакопеременные ряды. Теорема Лейбница о знакочередующемся ряде. Условная и абсолютная сходимость. Свойства условно и абсолютно сходящихся рядов.

Ряд вида ^∞∑ _n=1 (-1)ⁿ⁺¹ U_n называется знакочередующимся.

Теорема Лейбница - достаточный признак сходимости знакочередующегося ряда:

Если для знакочередующегося ряда ^∞∑ _n=1 (-1)ⁿ⁺¹ U_n выполняются условия:

1. абсолютные величины ряда убывают U₁ > U₂ > U₃ > …

2. (n->∞)lim │U _n│= 0

ряд сходится, причем его сумма положительна и не превосходит первого члена ряда.

Док-во:

Рассмотрим сумму первых членов ряда:

1) n – четное, то есть n = 2m => S _2m = U ₁ – U ₂ + U ₃ – U ₄ + … + U _2m-1 – U _2m = (U ₁ – U ₂) + (U ₃ – U ₄) + … + (U _2m-1 + U _2m) => согласно условию 1 мы получили, что S _2m > 0 ; S _2m = U ₁ – (U ₂ – U ₃) – (U ₄ – U ₅) - … - (U _2m-2 – U _2m-1) – U _2m => в силу 1-ого условия получим, что S _2m < U ₁ => последовательность частичных сумм (четных) возрастающая и ограничена сверху => по теореме Вейерштрасса

(n->∞)lim S _n = S.

2) n – нечетное => n = 2m + 1 => S _2m+1 = S _m + U _2m+1 => (m->∞)lim S _2m+1 = (m->∞)lim (S _2m + U _2m+1). (m->∞)lim S _2m = 0, (m->∞)lim U _2m+1 = 0 => 0 ≤ S _2m+1 ≤ U₁

Замечание:

Теорема Лейбница справедлива, если условие 1 выполняется, начиная с определенного элемента с номером N.

Замечание 2: Теорема Лейбница имеет следующий геометрический смысл

S₂ S₄ S S₃ S₁

Замечание 3: если знакочередующийся ряд удовлетворяет условию теоремы Лейбница, то можно оценить погрешность, кот. получим при замене S на Š. При замене S на Š мы отбрасываем все члены до U _n+1 . Эти члены образуют знакочередующийся ряд, кот. удовлетворяет теореме Лейбница => его сумма по модулю меньше первого члена ряда (U _n+1)

│S – S n│ < U n+1

Замечание 4: если знакочередующийся ряд не удовлетворяет условию 2 теоремы Лейбница, то ряд расходится.

Если знакочередующийся ряд удовлетворяет условию 2, но не удовлетворяет условию 1 т. Лейбница, то о его сходимости ничего сказать нельзя.

Пусть дан ряд ^∞∑ _n=1 U_n . Рассмотрим ряд ^∞∑ _n=1 │U_n │.

Теорема: если ряд ^∞∑ _n=1 │U_n │ сход-ся, то ^∞∑ _n=1 U_n - сход-ся абсолютно.

Док-во:

(n->∞)lim S _n = S – сумма ^∞∑ _n=1 U_n . (n->∞)lim T _n = T – сумма ^∞∑ _n=1 │U_n │ =>

S _n ⁺ - сумма только положительных. S _n = S _n ⁺ - S _n ^-

→ =>

S _n ^- - сумма только отрицательных. T _n = S _n ⁺ + S _n ^–

По условию ^∞∑ _n=1 │U_n │ - сход-ся => (n->∞)lim T _n = T

Т.к. S _n ⁺ и S _n ^– положительны и возрастают => {S _n ⁺} и {S _n ^-} – монотонны и ограничены => имеют предел => получим (n->∞)lim S _n = S ₁ – S ₂

Свойства:

1. Если ряды ^∞∑ _n=1 U_n и ^∞∑ _n=1 V_n сходятся абсолютно, то ряд

α ∙^∞∑ _n=1 U_n + β∙ ^∞∑ _n=1 V_n тоже сходится абсолютно.

Док-во:

α ∙^∞∑ _n=1 U_n + β∙ ^∞∑ _n=1 V_n = ^∞∑ _n=1 (α ∙ U_n + β ∙ V_n ) = ^∞∑ _n=1 │ α ∙ U_n + β ∙ V_n │, т.к.

│ α ∙ U_n + β ∙ V_n │≤ │α│ ∙│ U_n │ + │β│ ∙ │V_n │ => ^∞∑ _n=1 │U_n │ + ^∞∑ _n=1│ V_n │- сх-ся и ^∞∑ _n=1 │ α ∙ U_n + β ∙ V_n │ ≤ │α│^∞∑ _n=1 │U_n │ + │β│^∞∑ _n=1│ V_n │ => ^∞∑ _n=1 │ α ∙ U_n + β ∙ V_n │ - сход-ся

2. Для абсолютной сходимости ряда ^∞∑ _n=1 U_n необходимо и достаточно, чтобы его можно было представить в виде разности 2-х сходящихся знакополож-х рядов.

Док-во:

Необходимость: Пусть ^∞∑ _n=1 U_n сходится абсолютно =>

│U_n │, если U_n > 0

a _n = «фигурная скобка»

0, если U_n < 0

=> ^∞∑ _n=1 a _n и ^∞∑ _n=1 b _n - знакополож-ы

│U_n │, если U_n < 0

b _n = «фигурная скобка»

0, если U_n > 0

^∞∑ _n=1 U_n = ^∞∑ _n=1 a _n - ^∞∑ _n=1 b _n => оценим a _n и b _n

a _n ≤ │U_n │

=> ^∞∑ _n=1 │U_n │ - сход-ся => по первому признаку сходимости

b _n ≤ │U_n │ ^∞∑ _n=1 a _n и ^∞∑ _n=1 b _n тоже сходятся

Достаточность:

Пусть ^∞∑ _n=1 U_n - знакопеременный ряд.и ^∞∑ _n=1 U_n = ^∞∑ _n=1 a _n - ^∞∑ _n=1 b _n , где ^∞∑ _n=1 a _n и ^∞∑ _n=1 b _n сходятся => рассмотрим ^∞∑ _n=1 │U_n │ =>

│U_n │ = │ a _n - b _n │ ≤ │ a _n │+ │ b _n │= a _n + b _n

↓ ↓ ↓ ↓ ↓ ↓

сход-ся сход-ся сход-ся сход-ся сх-ся сх-ся

Следствие: условно сход-ся ряд является разностью 2-ч расходящихся знакополож-х рядов, для кот. выполняется необходимое условие сход-ти.

Док-во:

Пусть ^∞∑ _n=1 U_n - условно сход-ся => ^∞∑ _n=1 U_n = ^∞∑ _n=1 a _n - ^∞∑ _n=1 b _n причем оба ряда ^∞∑ _n=1 a _n и ^∞∑ _n=1 b _n расходятся. Иначе либо ^∞∑ _n=1 U_n - сход-ся абсолютно, если ^∞∑ _n=1 a _n и ^∞∑ _n=1 b _n - сходящиеся, либо ^∞∑ _n=1 U_n расходится как сумма сход-ся и расход-ся ряда.

Т.к. ^∞∑ _n=1 U_n сход-ся => (n->∞)lim U _n = 0 => (n->∞)lim a _n = 0 и (n->∞)lim b _n = 0.

Закон ассоциативности дял рядов: в любом сход-ся ряде любая группировка членов ряда, не изменяющая их порядка сохраняет сходимость ряда и величину суммы.

Док-во: Пусть ряд ^∞∑ _n=1 U_n (1) - сход-ся и его сумма S. Рассмотрим следующий ряд:

(2) (U₁ + U₂ + U₃ + … + U_b) + (U_b+1 + U_b+2 + U_b+3 + … + U_b+k) + (U_k+1 + U_k+2 + U_k+3 + … + U_n) + ... =>

Данный ряд получен из ряда ^∞∑ _n=1 U_n путем группировки членов при сохранении их порядка.

Введем S _n – частиная сумма (1)

T _n – частичная сумма (2) =>

T ₁ = S _b, T ₂ = S _b+k, T ₃ = S _n … => {T _n} является подпосл-тью послед-ти {S _n}, но т.к. ряд (1), то (n->∞)lim S _n = S. => (n->∞)lim T _n = S и {T _n} – сход-ся => ряд (2) тоже сход-ся и имеет ту же сумму.

Если ряд ^∞∑ _n=1 U_n сход-ся условно, то можно переставить его члены, то сумма получившегося ряда будет равна любому число, кот. задано предварительно.

Можно переставить так, что будет расходящимся.

^∞∑ _n=1 (-1)ⁿ⁺¹ ∙1/n – сход-ся условно. S = ln2

1- 1/2 + 1/3 – 1/4 + 1/5 – 1/6 + …

(1 – 1/2 – 1/4) + (1/3 – 1/6 – 1/8) + (1/5 – 1/10 – 1/12) + … + (1/2k-1 – 1/4k-2 – 1/4k) =

(1 – 1/2) – 1/4 + (1/3 – 1/6) – 1/8 + (1/5 – 1/10) – 1/12 + … + (1/2k-1 – 1/4k-2) – 1/4k =

1/2 (1 – 1/2 – 1/3 – 1/4 – 1/5 + … ) => (n->∞)lim S _n = 1/2∙S = 1/2 ∙ ln2

Пусть даны два ряда ^∞∑ _n=1 U_n и ^∞∑ _n=1 V_n. Составим следующую таблицу:

U₁V₁ U₁V₂ U₁V₃ … U₁V_n

U₂V₁ U₂V₂ U₂V₃ ... U₂V_n

..................................................

U_nV₁ U_nV₂ U_nV₃ ... U_nV_n

Под произведением двух рядов ^∞∑ _n=1 U_n и ^∞∑ _n=1 V_n понимают ряд, составленный порядок членов выбран согласно следующей схеме:

=>

U₁V₁ + (U₁V₂ + U₂V₁) + ... + (U₁V_n + U₂V_n-1 + … + U_n-1V₂ + U_nV₁)

Если ряды сход-ся абсолютно и их суммы равны V и U =>

^∞∑ _n=1 U_n ∙ ^∞∑ _n=1 V_n = U ∙ V

Достаточные условия сходимости рядов ^∞∑ _n=1 a _n b _n :

Признак Дерехле: Если последовательность { a _n } – монотонная и (n->∞)lim a _n = 0, а послед-ть частичных сумм { b _n } – ограничена => ^∞∑ _n=1 a _n b _n - сход-ся.

Признак Абеля: Если последовательность { a _n } – монотонна и ограничена, а ряд ^∞∑ _n=1 b _n – сходящийся => ^∞∑ _n=1 a _n b _n – сход-ся.

Док-во: { a _n } – монотонна и ограничена => по признаку Вейерштрасса (n->∞)lim a _n = a. Рассмотрим послед-ть { a _n - a } и (n->∞)lim (a _n - a) = 0. Т.к. ^∞∑ _n=1 b_n – сход-ся, то послед-ть его частичных сумм { b _n } – сход-ся => ^∞∑ _n=1 ( a _n - a ) b_n по признаку Дерехле тоже сход-ся => ^∞∑ _n=1 a _n b _n - a ∙ ^∞∑ _n=1 b _n => ^∞∑ _n=1 a _n b _n =

^∞∑ _n=1 ( a _n - a ) b_n + a ∙ ^∞∑ _n=1 b _n => ^∞∑ _n=1 a _n b _n - сход-ся.

↓ ↓

сход-ся сход-ся

3. Функциональные ряды: опреедление, область сходимости функционального ряда. Сумма функционального ряда.

Выражение U₁(x) + U₂(x) + … + U_n(x) + … (1) называется функциональным рядом и обозначается ^∞∑ _n=1 U _n (x)

Функции U₁(x), U₂(x), …, U_n(x) называются членами ряда, при этом U _n(x) называется общим членом ряда.

Придавая в выражении (1) переменной x некоторые значения x₀ принадлежащие x мы получим числовой ряд:

(2) U₁(x₀) + U₂(x₀) + … + U_n(x₀) + … = ^∞∑ _n=1 U _n (x₀)

В зависимости от значения x₀ ряд (2) может оказаться сходящимся или расходящимся.

Множество тех значений x₀ принадлежащих x, для которых (2) сходится, называется областью сходимости ряда ^∞∑ _n=1 U _n (x), =>

Пусть D – область сходимости функционального ряда (1), x₀ принадлежит D => ^∞∑ _n=1 U _n (x₀) – сходится.

Обозначим сумму ряда через S₀. Функция S(x) определенная в области D и принимающая в каждой точке x₀ этой области значение S₀ называется суммой ряда.

Пр-р: 1) 1 + x + x² + x³ + … + xⁿ = ^∞∑ _n=0 xⁿ =>

Придавая x значения x₀ получим числовой ряд ^∞∑ _n=1( x₀)ⁿ . Это ряд геометрической прогрессии с первым членом a₀ = 1 и знаменателем q = x₀. т.к. ряд геометрической прогрессии сходится, если │q│=│x₀│< 1=>область сходимости для этого ряда (-1; 1)

Для данного функционального ряда можно найти и сумму. Сумма числового ряда ^∞∑ _n=1( x₀)ⁿ равна 1/(1- x₀) => функция S(x) = 1/(1 - x), где x принадлежит (-1; 1).

Сумму функционального ряда можно ввести иначе: как предел некоторой функциональной последовательности, т.е. запишем

S₁(x) = U₁(x)

S₂(x) = U₁(x) + U₂(x) S₃(x) = U₁(x) + U₂(x) + … + U_n(x) => придадим x=x0 принадлежащее D => получим последовательность частичных сумм числового ряда ^∞∑ _n=1 U _n (x₀) =>

S(x) – сумма ^∞∑ _n=1 U _n (x) => S(x) = (n->∞)lim S _n (x)

2) ^∞∑ _n=1 sin(nx)/n² => областью сходимости этого ряда будет вся числовая ось. Действительно, придавая x любое значение x₀ получим числовой ряд ^∞∑ _n=1 sin(nx₀)/n²

=> Рассмотрим ряд ^∞∑ _n=1 │sin(nx₀)│/n², т.к. для любого n верно, что

│sin(nx₀)│/n² ≤ 1/n², и ряд ^∞∑ _n=1 1/n² – сход-ся, то по первому признаку сравнения рядов: ^∞∑ _n=1 │sin(nx₀)│/n² – сход-ся => ряд ^∞∑ _n=1 sin(nx)/n² сходится абсолютно для любого x.

4. Равномерная сходимость функциональных рядов.

Пример: ряд является рядом геометрической прогрессии с первым членом 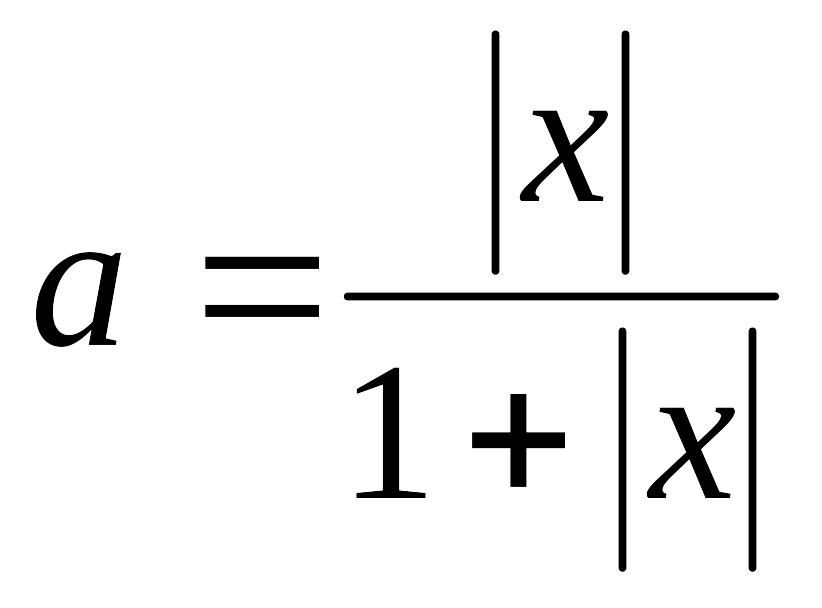и знаменателем . Если , то и ряд в этих точках сходится. Сумма функционального ряда в этих точках будет равна:

. С другой стороны, если , то соответствующий числовой ряд тоже сходится и его сумма будет равна 0. Т.о., получаем, что областью

сх-сти данного ряда является вся числовая ось, а его суммой – функция . Эта функция в точке терпит разрыв, хотя все функции в этой точке непрерывны.

Пусть дана некоторая пос-ть функций с общей обл.опр. Х: (3).

Придавая переменной х значения х₀ получим некоторую числовую пос-ть: (4). Мн-во D тех значений х₀, для которых числовая пос-ть (4) сходится, называется областью сходимости функ-ной пос-ти (3). Ф-ю , опред-ную в области D и принимающую в каждой точке х₀ этой области значение назыв. пределом функциональной пос-ти (3).

Сумму функ-го ряда можно ввести иначе: как предел некоторой функ-ной пос-ти. Действительно, запишем пос-ть функций: , , . Придавая переменной х значение , получим числовую пос-ть . Это будет пос-ть частичных сумм числового ряда . Пусть - сумма ряда . Тогда , т.е. для любого , .

По определению это означает, что .

В общем случае номер N зависит от и от х₀

df: (равномерная сх-ть) Если и , то говорят, что ряд сходится в области Δ равномерно.

th: (признак равномерной сходимости Вейерштрасса). Если найдется сходящийся числовой ряд такой, что выполняется н-во , n=1,2,3,…(6), то функ. ряд сходится в области D равномерно.

Если для функ. ряда в области D выполняется н-во (6), то говорят, что функ. ряд мажорируется в области D числовым рядом . Ряд называют при этом мажорирующим рядом (или мажорантой).

Замечание: признак Вейерштрасса достаточный, но не необходимый, т.е. существуют равномерно сходящиеся ряды, для которых не удается подобрать мажорирующего ряда. Равномерно сходящиеся ряды, для которых можно найти мажорирующий сходящийся ряд, часто называют правильно сходящимися.

Свойства равномерно сходящихся рядов:

1) Если ряд сходится в области D равномерно и все члены ряда в этой области непрерывны, то сумма ряда тоже будет непрерывна в области D.

2) Если ряд сходится в области D равномерно и все члены ряда в этой области непрерывны, то ряд сходится в области D равномерно, и справедливо неравенство: (7), где - сумма ряда .

Замечание: Так как - сумма ряда , то можно записать = . Но тогда неравенство (7) можно переписать в виде: , поэтому говорят, что равномерно сходящийся ряд непрерывных функций можно почленно интегрировать на любом отрезке .

3) Пусть ряд сходится в области D и - его сумма. Если все члены этого ряда в области D непрерывно дифференцируемы и ряд сходится в D равномерно, то ряд тоже сходится в области D равномерно, и его сумма является функцией непрерывно дифференцируемой и имеет место равенство (8).

Замечание: Равенство (8) можно записать в виде . Поэтому говорят, что если ряд производных сходится в области D равномерно, то исходный ряд тоже сходится в D равномерно и его можно почленно дифференцировать.

4) Пусть ряд сходится в области D равномерно. Если - ограниченная в области D функция, то ряд тоже будет сходиться в области D равномерно