5. Степенной ряд.
df:
(определение)Степенным рядом по степени
называют функциональный ряд вида
,
(1) где
,
а- коэфф. степенного ряда. Если
,
то
(2)
Ряд называется степенным рядом по степени х.
Сходимость степенных рядов.
th
(теорема Абеля): Если степенной ряд
сходится при
,
то он сходится абсолютно для всех х
таких, что:
.
Док-во:
- сходится по условию.
такое,
что все члены
ряда по абс. величине меньше М. Ряд
перепишем
в виде:
.
Рассмотрим
соотв. ряд из абс. величин:
(т.к.
по модулю
,
)
данный ряд будет сходиться, если
.
Следствие:
Если степенной ряд расходится в точке
,
то он расходится
.
Док-во:
пусть данный ряд сходится в какой-то
точке
,
значит по теореме Абеля
он
должен сходиться в
,
но это противоречие.
Если
,
в которой ряд сходится, то сущ.интервал
внутри, симметричный отн. начала
координат, в котором ряд сх-ся. Аналогично
с расх-ю.
.
Число R называют радиусом
сходимости степенного ряда (2). Интервал
(-R;R) называют
интервалом сходимости. Если х=0, то инт.
вырождается в точку. Если ряд (2) не имеет
точек расх-ти, то
.
На концах интервала сходимости, т.е.
,
вопрос сходимости решается индивидуально
для каждого ряда.
Замечание: Для степенных рядов вида
(1) все остается в силе с той лишь разницей,
что центр интервала сходимости будет
.
Поскольку внутри области сходимости ряд (2) сходится абсолютно, то его ряд модулей (3) имеет тот же радиус сходимости.
Для определения области сходимости ряда модулей (3), который является знакоположительным, воспользуемся признаком Даламбера:
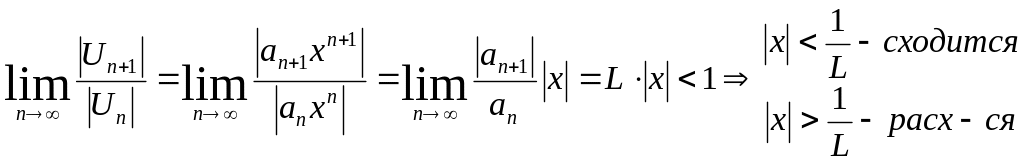(5).
Ряд
(2) сходится абсолютно при
и расходится при
радиус
сходимости
.
Для нахождения интервала абсолютной сходимости можно воспользоваться также признаком Коши.
6. Теорема Дирихле
Пусть фу-ия y=f(x) на интервале [-П,П] имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва 1-го рода(Точек конечного скачка функции). Тогда ряд Фурье этой фу-ии сходится в каждой точке интервала [-П,П] и его сумма S(x) удовлетворяет условиям:
В каждой точке непрерывности фу-ии ряд Фурье сходится к значению функции в этой точке S(x)=F(x).
В каждой точке конечного разрыва функции сумма ряда Фурье = полусумме односторонних пределов фу-ии в этих точках S(x)=1/2[f(x0-0)+f(x0+0)].
В конечных точках интервалов периодичности фу-ии сумма ряда Фурье также равна среднему арифметическому соответствующих односторонних пределов S(x)=1/2[f(-П-0)+f(П+0)].
Теорема 1 (Дирихле): Пусть на [-l;l] функция f(x) удовлетворяет двум условиям, которые называются условиями Дирихле:
1.Функция Дирихле непрерывна или имеет конечное число точек разрыва первого рода
2.Функция монотонна или имеет конечное число точек экстремумов.
Тогда тригонометрический ряд Фурье функции f(x) сходится во всех точках отрезка и его суммой будет S(x), которая вычисляется по следующей формуле