1. Основні властивості нескінченно малих послідовностей.

2. Теорема Больцано–Вейєрштрасса про обмежену послідовність.

3. Поняття фундаментал послідовності. Фундаментал збіжної послід.

4. Єдиність границі послідовності.

5. Перехід до границі послідовності у нерівностях.

6. Монотонні послідовності. Ознака збіжності монотонної послідовності.

7. Теореми про границю суми,добутку,відношення числових послід.

8. Критерій Коші збіжності числової послідовності.

9. Число як границя збіжної монотонної послідовності.

10. Означ за Коші границі функції. Еквівал означень за Коші та за Гейне.

11. Означення за Гейне границі функції. Точка дотикання множини.

12. Властивості границь функцій.

13. Нескінченно малі функції.

14. Порівняння функцій в околі заданої точки. Символи Ландау.

15. Критерій Коші існування границі функції.

16. Границі монотонних функцій.

17. Перша чудова границя.

18. Друга чудова границя.

19. Еквівалентні функції.

20. Поняття неперервності функції в точці. Одностороння неперервність.

21. Різні форми запису неперервності функції в точці.

22. Неперервність оберненої функції.

23. Теорема Вейєрштрасса про неперервну на відрізку функцію.

24. Теорема Больцано –Коші про проміжні значення неперервної функції.

25. Поняття похідної. Геометрич,механічний та екон зміст похідної.

26. Зв’язок неперервності та диференційованості.

27. Необхідна та достатня умова диференційованості функції.

28. Поняття диференціалу. Геометрич та механіч зміст диференціалу.

29. Похідна суми, добутку, відношення функцій.

30. Похідна суми, добутку, відношення функцій.

31. Похідна оберненої функції.

32. Властивості диференціалу. Інваріантність форми першого диференц.

33. Похідні основних елементарних функцій.

34. Похідні вищих порядків, їх властивості.

35. Диференціали вищих порядків, їх властивості.

36. Теорема Ферма.

37. Теорема Ролля, її геометричний зміст.

38. Теорема Лагранжа про скінчений приріст, її геометричний зміст.

39. Теорема Коші про середнє значення.

40. Перше правило Лопіталя.

41. Формула Тейлора та Маклорена з залишков членом у формі Пеано.

42. Формула Тейлора з залишковим членом у формі Лагранжа.

43. Необхідна та достатня умова монотонності функції на інтервалі.

44. Екстремум функції. Необх умова внутрішн локального екстремуму.

45. Достатні умови екстремуму (використання першої похідної).

46. Достатні умови екстремуму (використання похідних вищих порядків).

47. Опуклість функції. Геометричне визначення за допомогою хорд.

48. Необхідні та достатні умови опуклості функції.

49. Поняття точки перегину. Необхідні умови точки перегину.

50. Достатні умови точки перегину.

51. Поняття асимптоти. Визначення параметрів похилої асимптоти.

52. Лема про ф-ї, що мають однак похідні на інтервалі.Поняття первісної ф-ї. Поняття невизнач інтегралу, його властивості. Таблиця інтегралів.

53. Заміна змінної у невизначеному інтегралі та інтегрування частинами.

54. Інтегрування раціональних дробів.

55. Інтегрування тригономет виразів,універсал тригонометр підстановка.

56. Інтегрування найпростіших ірраціональних функцій.

57. Поняття інтегральної суми. Поняття визначеного інтеграла Рімана. Необхідна умова інтегрованості функції за Ріманом.

58. Поняття верхньої та нижньої сум Дарбу. Властивості сум Дарбу. Формулювання критерію інтегрованості. Приклади застосування.

59. Поняття рівномірно неперервної функції. Формулювання теореми Кантора про рівномірну неперервність неперервної функції. Інтегрованість неперервної функції.

60. Інтегрованість функції, монотонної на відрізку. Інтегрованість обмеженої функції, що має скінчену кількість точок розриву.

61. Властивості визначеного інтегралу, що пов’язані з підінтегральною функцією, з відрізком інтегрування і визначені нерівностями.

62. Теореми про середнє значення інтеграла Рімана.

63. Неперервна залежність визначеного інтегралу від змінної верхньої границі. Похідна інтегралу по змінній верхній границі. Формула Ньютона – Лейбніца.

64. Заміна змінної у визначеному інтегралі, її геометричний зміст.

65. Формула інтегрування частинами для визначеного інтегралу.

66. Поняття площі плоскої фігури.

67. Критерій квадровності плоскої фігури. Приклад необмеженої фігури скінченої площі.

68. Обчислення площ і довжин дуг кривих. Обчислення об’ємів просторових фігур.

69. Невласні інтеграли першого і другого роду. Критерій Коші збіжності невласного інтегралу.

70. Невласні інтеграли від невід’ємних функцій.

71. Абсолютно і умовно збіжні невласні інтеграли. Приклади.

72. Ознаки збіжності та розбіжності невласних інтегралів. Еталонні інтеграли.

73. Ознаки Діріхле та Абеля збіжності невласного інтеграла.

1. Основні властивості нескінченно малих послідовностей.

О1. Послідов α_n назив НМП 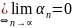. Тобто .

Власт1: - НМП ({x_n} - збіжна)

Довед: 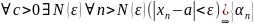– НМП

Власт2: Скінченна лін комб НМП є НМП

Довед: Розглянемо 2 послід, які є НМП. Нехай {α_n} I {β_n} НМП .

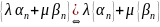
Власт3: Добуток НМП на обмеж послідов є НМП

Довед: Нехай {x_n} - обмеж, {α_n} – НМП. Доведемо, що {x_n, α_n} – НМП

{x_n} - обмеж

{α_n} – НМП

Наслідок: Добуток скінченного числа НМП є НМП.

Довед: нехай {α_n}, {β_n}-НМП. {β_n} НМП→{β_n} збіж→{β_n} обмеж. Тобто {α_n}-НМП, {β_n} обмеж →за вл 3 {α_n, β_n} – НМП.

Власт4: 1)якщо послід {x_n} нескінченно велика, то почин з деякого номера послід {1/x_n} - НМП.

2)якщо послід {α_n} НМП, α_nне=0 – НВП.

Довед: {x_n} НВП

2. Теорема Больцано-Вейєрштрасса

Озн:Нехай задана ЧП . Підпослід цієї послід назив послід , яка утвор з членів заданої послід так,що номери йдуть в порядку зрост.

-це номер члена підпослід в заданій послід;k -номер члена підпослід.

Теорема Б-В1)З б-я обмеж ЧП можна виділити збіжну підпослід.2)З б-я необм зверху(знизу)ЧП можна виділ підпослід,що має границею +∞,-∞.

Доведення 1)Принцип компактності числової прямої.Задано – обмеж. _. -деякий член послідовності. Поділимо відрізок навпіл та позначимо ту половину, яка містить нескінч к-сть членів послідовності :

Вибираємо елем , - член нашої послід і . Вибираємо елемент

Через к кроків маємо к=0,1,2.......

к=1,2,3...., Зауважимо, що

Отже, с-ма відрізків є с-мою вкладених стяжних відрізків, тому існує єдина точка ξ, яка належить перетину всіх цих відрізків, причому ( 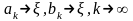) - збіжна. Доведено.

2) -необмежена зверху.

................................................

с=k

_{За наслідком} леми про міліц маємо

3. Поняття фундамент послідов.Фундаментальність збіж послідов.

Послідов назив ф. якщо

Права частина означення називається умовою Коші.

І нша форма умови Коші:

Лема1 Якщо послідовність збіжна, то вона ф.Доведення: Нехай

, - фундаментальна за означенням

Лема2.Якщо послід ф,то вона обмеж.

_{Доведення}:В умові Коші покладемо 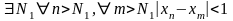Виберемо , тоді _.

Оберемо . Отже,

,

Лема3:Якщо деяка підпослід ф послід збіжна,то її границя є гран усієї ЧП.

Доведення: Нехай - фундаментальна.

За умовою Коші

Оберемо так, щоб виконувалось

Перейдемо до границі, коли Критерій КошіДля того,щоб посл мала скінч lim необх і дост, щоб вона була ф.

- Ф. Доведення: Необх довед в лемі 1. Доведемо достат. - ф - обмежена Критерій Коші дає необх і дост умову збіжності послід в термінах тільки самих членів послідовності без використання значення границі.

Теорема Штольца.Нехай послід 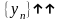і нескінч велика. Нехай послід має границю, тоді послід теж має границю, та

4. Єдиність границі послідовності.

Теорема. Послідовність точок розширеної числової прямої може мати на цій прямій лише одну границю.(Якщо послід має lim, то він один)

Доведення (від супротивного):

Нехай є ; і , , aне=b

Тоді:

a<b ---- і , що не перетинаються ( =Ø)

x_n при n→∞ →a ---- 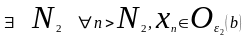_{---зовні околу лежить скінченне число членів послід х1, х2,…,хN1. Це означ, що в може попасти лише скінченна к-сть членів послід, що супереч означ границі хn→b при n→∞.}

В силу того, що околи не перетинаються записані співвідношення не можливі, маємо суперечність.