Вопрос 2. Определение ускорения точки при естественном способе задания движения. Касательное и нормальное ускорения точки.

Определим проекции ускорения точки на естественные координатные оси. Для этого представим вектор скорости точки по формуле:

.

Определим ускорение точки, продифференцировав по t произведение двух переменных величий и умножив первое слагаемое на :

_

З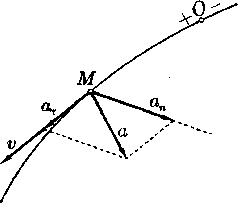 ная, что и

Подставив эти выражения, получим вектор ускорения в виде

Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением, а другой направлен по касательной и называется касательным ускорением точки:

где нормальное ускорение точки

а касательное ускорение точки

Скалярные множители и , определяющие нормальное и касательное ускорения точки, представляют собой проекции ускорения точки на главную нормаль и касательную.

Проекция ускорения точки на бинормаль оказалась равной нулю, т. к. вектор ускорения расположен в соприкасающейся плоскости.

Согласно формуле (73.3),

т е проекция ускорения точки на главную нормаль равна квадрату модуля ско­рости точки, деленному на радиус кривизны траектории в соответствующей точке. Эта проекция всегда положительна. Из этого следует, что нормальное ускорение точки всегда направлено к центру кривизны траектории и равно по модулю этой проекции.

Условимся алгебраическую величину касательного ускорения обозначать , а его модуль .

Согласно формуле ,

т е проекция ускорения точки на касательную равна второй производной от дуговой координаты точки по времени или первой производной от алгебраиче­ской величины скорости точки по времени.

Эта проекция имеет знак плюс, если направления касательного ускорения точки и орта совпадают, и знак минус, если они противоположны.

Таким образом, в случае естественного способа задания движения, когда из­вестны траектория точки, а следовательно, ее радиус кривизны в любой точке и уравнение движения s = f(t), можно найти проекции ускорения точки на есте­ственные оси и по ним определить модуль и направление ускорения точки:

; ;

где и — углы, образованные направлением ускорения с принятыми направлениями касательной и главной нормали в данной точке.

Если проекции скорости и касательного ускорения на касательную v = ds и имеют одинаковые знаки, то и направление этих векторов совпадают, т. е точка движется ускоренно.

Если же их проекции v = ds и имеют различные знаки, то и направления этих векторов противоположны, т. е. точка движется замедленно.

Вопрос 3. Некоторые частные случаи движения точки.

Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.

1) Прямолинейное движение. Если траекторией точки является прямая линия, то . Тогда и все ускорение точки равно одному только касательному ускорению:

Так как в данном случае скорость изменяется только численно, то отсюда заключаем, что касательное ускорение характеризует изменение скорости по численной величине.

2) Равномерное криволинейное движение. Равномерным называется такое криволинейное движение точки, в котором численная величина скорости все время остается постоянной:

v= const. Тогда и все ускорение точки равно одному только нормальному ускорению:

Вектор ускорения направлен при этом все время по нормали к траектории точки.

Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормальное ускорение характеризует изменение скорости по направлению.

Найдем закон равномерного криволинейного движения. Известно, что или ds = v dt.

Пусть в начальный момент (t=0) точка находится от начала отсчета на расстоянии s₀. Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим

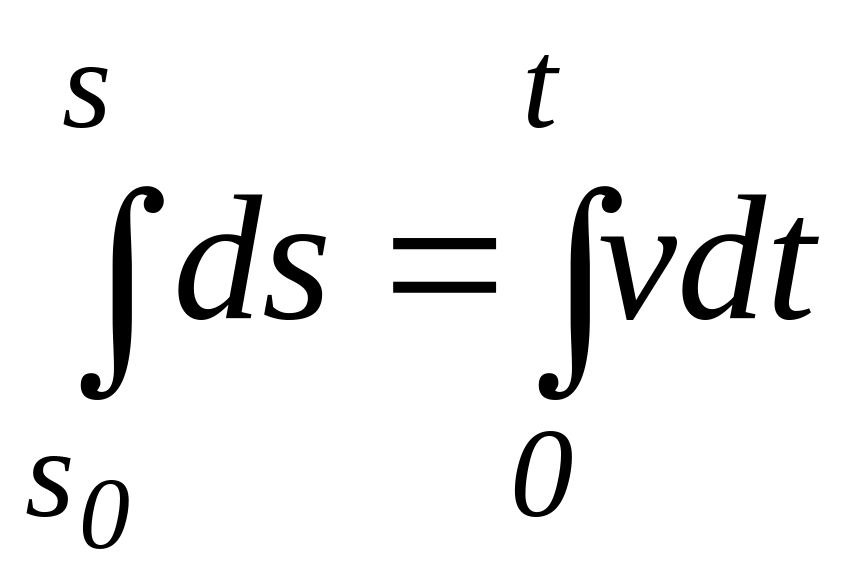или

так как v = const. Окончательно находим закон равномерного криволинейного движения точки в виде

s = s_{0 +} vt.

Если положить s₀ = 0, то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, растет пропорционально времени, а скорость движения равна отношению пути ко времени

3) Равномерное прямолинейное движение. В этом случае _n = _τ = 0, а значит и =0. Заметим, что единственным движением, в котором ускорение точки все время равно нулю, является равномерное прямолинейное движение.

4) Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: = const. Найдем закон этого движения, считая, что при t=0 s=s₀ , a v=v₀ , где v₀ - начальная скорость точки.

Согласно формуле или dv= _τdt

Так как _τ = const, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:

v=v₀ + _τt .

Эту формулу представим в виде

или

Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде

Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает замедленным. Так как изменение модуля скорости характеризуется касательным ускорение, то движение будет ускоренным, если величины v и , имеют одинаковые знаки (угол между векторами и острый), и замедленным, если разные (угол между и тупой).

Задача

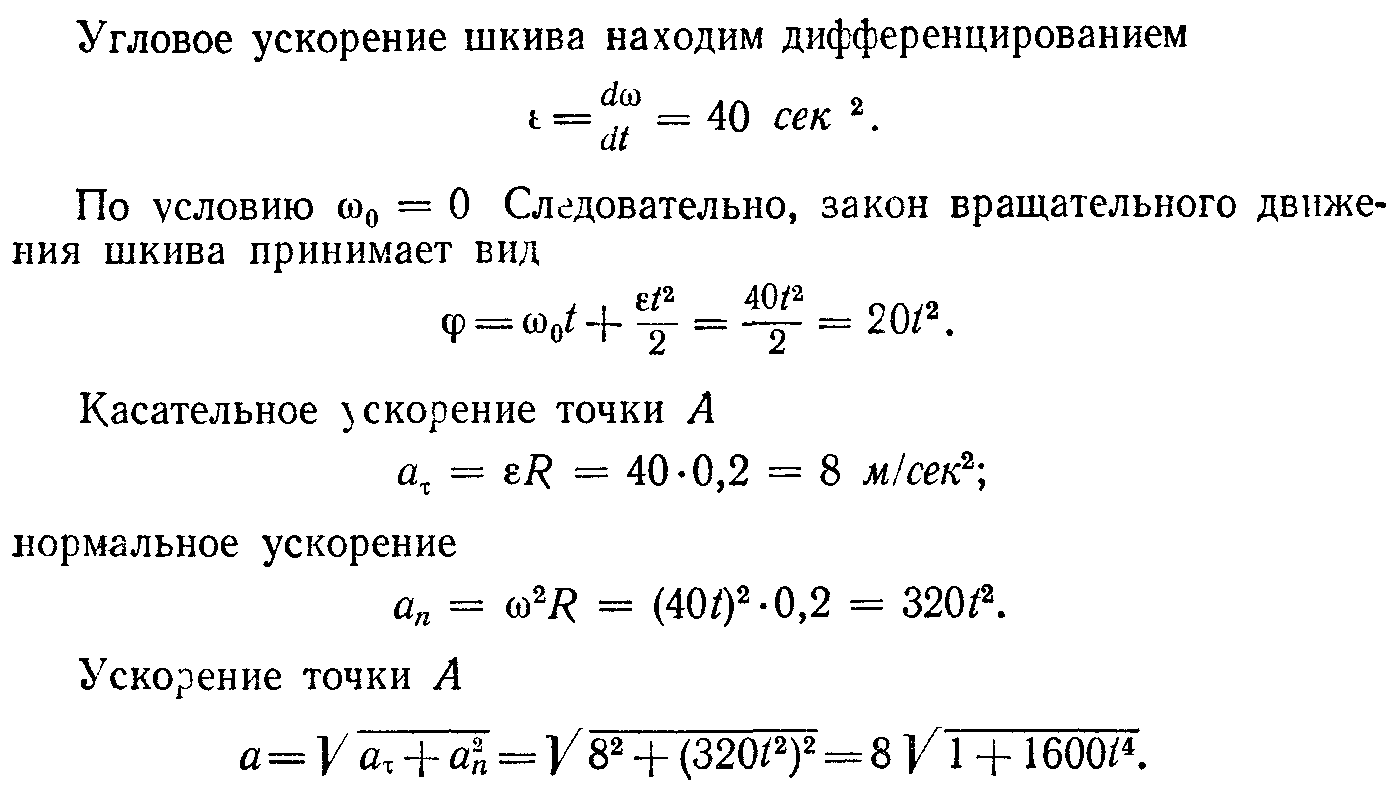
III. ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ (2 минуты):

Доведение общих выводов по лекции. Ответы на неясные вопросы. Задание на самоподготовку. Заполнение журнала (журналов) учебных групп.

доцент кафедры “Теоретическая механика”

кандидат технических наук, доцент

Д.Н. Миронов