БЕЛОРУСКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Теоретическая механика»

ЛЕКЦИЯ

по учебной дисциплине

«Теоретическая механика»

Раздел II. «Кинематика»

Тема № 2.2. «Кинематика точки»

Лекция № 11

«Ускорение точки»

Минск-2010г.

УЧЕБНЫЕ И ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ:

1. Ознакомиться с ускорением точки при различных способах задания движения.

2. Изучить касательное и нормальное ускорения точки.

3. Воспитание у обучаемых общей и технической культуры, чувства гордости за выбранную воинскую профессию.

УЧЕБНЫЕ ВОПРОСЫ:

1. Ускорение точки при различных способах задания движения. Естественные координатные оси. Вектор кривизны.

2. Определение ускорения точки при естественном способе задания движения. Касательное и нормальное ускорения точки.

3. Некоторые частные случаи движения точки.

ВРЕМЯ: два академических часа

МЕСТО: учебная аудитория

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПРЕПОДАВАТЕЛЮ:

Изложение материала проводится в сочетании дедуктивного (от общего к частному – определения, анализ формул и т.п.) и индуктивного (от частного к общему – вывод формул, примеры работы механизмов и т.п.) методов. Рассматриваемые вопросы иллюстрируются плакатами и макетами механических устройств.

Активизация работы обучаемых достигается проблемным изложением материала, путём постановки и решения проблемных вопросов и задач, а также использование продуктивных методов обучения: частично-поискового и исследовательского.

Воспитательные цели достигаются личным примером преподавателя, требовательностью в выполнении руководящих документов и проведением информационной работы в идеологической и научно-технической области.

УЧЕБНО-МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ: плакаты.

УЧЕБНАЯ ЛИТЕРАТУРА:

1. Курс теоретической механики / Под ред. К.С. Колесникова. М: Изд-во МГТУ им. Н.Э. Баумана, 2000 г.

2. Никитин Н.Н. Курс теоретической механики: Учебник. – М.: Изд-во Высшая школа, 1990 г. 600 стр.

3. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Статика. Кинематика. Динамика. – М.: Интеграл-ПРЕСС, 2006.

4. Тульев В.Д. Теоретическая механика. Статика и кинематика. – Мн.: Книжный дом, 2004.

5. Хижняк Е.И. Теоретическая механика. Методические рекомендации курсантам по подготовке к занятиям. Ч.III. – Мн.: ВА РБ, 2006.

План лекции:

I. ВСТУПИТЕЛЬНАЯ ЧАСТЬ (3 минуты):

Проверка наличия обучаемых, внешнего вида и их готовность к занятию (наличие конспектов и чертежных принадлежностей).

Объявление темы, учебных вопросов и целей занятия, практической значимости тематики нового материала в изучении дисциплин по профилю обучения.

II. ОСНОВНАЯ ЧАСТЬ (85 минут):

Вопрос 1. Ускорение точки при различных способах задания движения.

Ускорение точки можно задать тремя способами:

1. векторный;

2. координатный;

3. естественный.

Векторный способ задания движения.

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.

Пусть в некоторый момент времени t движущаяся точка находится в положении М и движется со скорость , а в момент t₁ находится в положение M₁ и имеет скорость (рис. 1).

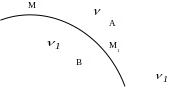
Рисунок 1

Тогда за промежуток времени скорость точки получает приращение . Для построения вектора отложим от точки М вектор, равный , и построим параллелограмм, в котором диагональю будет , а одной из сторон . Тогда, очевидно, вторая сторона и будет изображать вектор . Заметим, что вектор всегда направлен в сторону вогнутости траектории.

Отношение приращения вектора скорости к соответствующему промежутку времени определяет вектор среднего ускорения точки за этот промежуток времени:

(1)

Вектор среднего ускорения имеет, очевидно, то же направление, что и вектор , т. е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется векторная величина , к которой стремится среднее ускорение при стремлении промежутка времени Δt к нулю:

,

или, с учетом определения скорости из предыдущей лекции

(2)

Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Размерность ускорения - длина/(время)²; в качестве единицы измерения применяется обычно м/сек².

Из формулы (2) следует также, что вектор ускорения точки равен отношению элементарного приращения вектора скорости к соответствующему промежутку времени dt.

Найдем, как располагается вектор по отношению к траектории точки При прямолинейном движении вектор направлен, очевидно, вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения , так же как и вектор , лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор будет направлен в сторону вогнутости траектории и будет лежать в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке M₁. В пределе, когда точка M₁ стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Ускорения точки при координатном способе задания движения.

Рисунок 2

Вектор ускорения точки Отсюда на основании теоремы о проекции производной получаем:

(3)

или (4)

т.е. проекции ускорения точки на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул:

(5)

где α₁, β₁, γ₁ – углы, образуемые вектором ускорения с осями координат.

В случае же прямолинейного движения, которое задается одним уравнением x=f(t), будем иметь

(6)

Так как проекции на другие оси отсутствуют, то, следовательно, в данном случае т. е. при прямолинейном движении формулы (9) непосредственно определяют скорость и ускорение точки.

Естественные координатные оси. Вектор кривизны.

Проведем в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную касательной, и спрямляющую плоскость, перпен­дикулярную соприкасающейся и нормальной плоскостям, образующую с этими плоскостями естественный трехгранник (рис. 3).

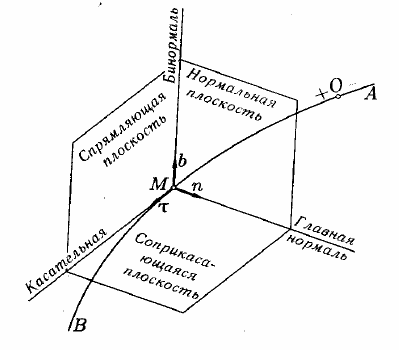
Рисунок 3

Линия пересечения соприкасающейся и нормальной плоскостей называется главной нормалью кривой.

Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью кривой.

Естественными координатными осями называются три взаимно перпендикулярные оси; касательная, направленная в сторону возрастания дуговой координаты, главная нормаль, направленная в сторону вогнутости кривой, и бинормаль, направленная по отношению к касательной и главной нормали так же, как ось Оz направлена по отношению к осям Ох и Оу в правой системе координатных осей. Единичные векторы-орты этих осей обозначаются соответственно и . Естественные координатные оси имеют начало в точке М кривой и при движении точки М по этой кривой перемещаются вместе с ней, оставаясь взаимно перпендикулярными, но изменяя свое направление в пространстве.

Возьмем на кривой АВ две точки М и М₁, соответствующие дуговым координатам ОМ = s и ОM₁ = s + Δs. Покажем орты касательной и в этих точках (рис. 4). Модуль орта , равный единице, постоянен, но направление орта изменяется при перемещении точки по кривой, т. е. орт является переменным вектором.

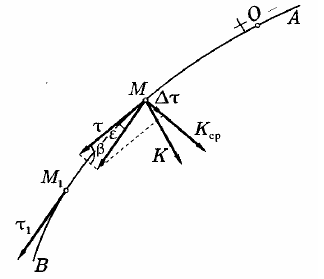
Рисунок 4

Определим приращение орта на участке ММ₁ = ∆s. Для этого отложим от точки М орт и построим при этой точке параллелограмм, одной из сторон которого будет орт , а диагональю — орт . Тогда другая сторона параллелограмма будет приращением орта , т. к. .

Разделим приращение орта на приращение дуговой координаты ∆s. Вектор характеризующий поворот касательной к кривой на участке ММ₁, называется вектором средней кривизны кривой на участке ММ₁. Этот вектор имеет направление вектора , т. е. направлен в сторону вогнутости кривой.

Предел , к которому стремится вектор средней кривизны кривой , когда ∆s стремится к нулю, называется вектором кривизны кривой в данной точке:

.

Орт касательной к кривой является вектор-функцией дуговой координаты s, т. к. его направление зависит от положения точки на кривой, т. е.

Тогда

Следовательно, вектор кривизны кривой в данной точке равен производной от орта касательной к кривой по дуговой координате.

Для определения модуля этого вектора рассмотрим равнобедренный треугольник, образованный , и (рис. 4).

Угол между направлениями касательных в двух точках кривой М и М₁ называется углом смежности. При малом расстоянии ∆s угол смежности тоже мал.

Модуль найдем как длину основания равнобедренного треугольника с малым углом при вершине и боковыми сторонами, равными единице.

Тогда

Модуль вектора кривизны К определяется по формуле

Из дифференциальной геометрии известно, что предел отношения угла смежности к приращению дуговой координаты при стремлении к нулю равен кривизне кривой , при - радиус кривизны кривой в точке М.

Установим также направление вектора кривизны.

Вектор средней кривизны находится в плоскости треугольника, составленного векторами , и , предельным положением которого является соприкасающаяся плоскость. Следовательно, вектор кривизны расположен в соприкасающейся плоскости.

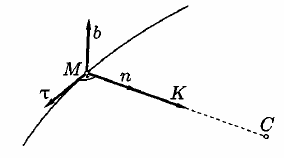
Рисунок 5

Рассмотрим угол , составленный вектором с касательной в точке М (рис. 4):

2β = 180° - ε; β = 90° - ε /2.

При приближении точки M₁ к точке М угол смежности ε стремится к нулю, а поэтому

Так как вектор кривизны расположен в соприкасающейся плоскости и пер­пендикулярен орту , то он направлен по главной нормали к центру кривизны кривой (рис. 5).

Представим вектор в виде произведения орта на модуль этого вектора:

где р = МС — радиус кривизны кривой в данной точке М.