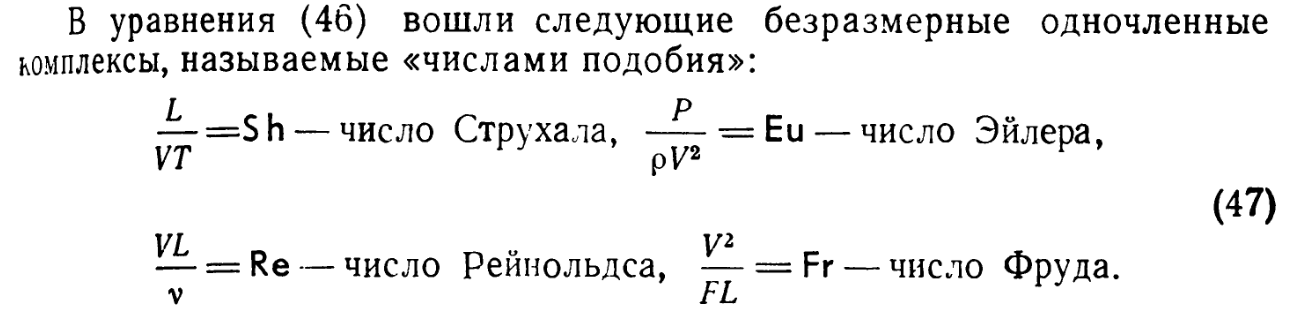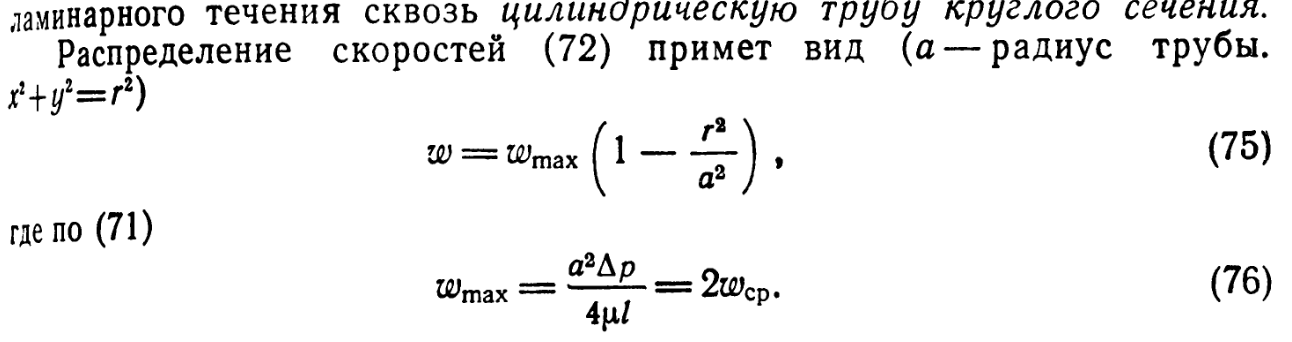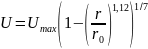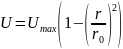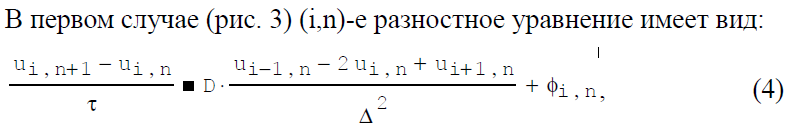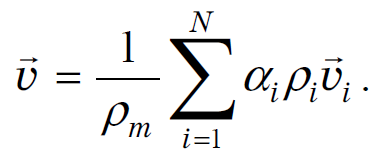7. Уравнение подобия. Определяемые и определяющие критерии и числа подобия.

Физические явления, процессы или системы подобны, если в сходственные моменты времени в сходственных точках пространства значения переменных величин, характеризующих состояние одной системы, пропорциональны соответствующим величинам другой системы. Коэффициенты пропорциональности для каждой из величин называется коэффициентом подобия.

Если в рассматриваемых физических явлениях или системах существует равенство не всех, а лишь некоторых независимых критериев подобия, то говорят о неполном, или частичном, подобии. Такой случай наиболее часто встречается на практике.

Размерные физические параметры, входящие в критерии подобия, могут принимать для подобных систем сильно различающиеся значения; одинаковыми должны быть лишь безразмерные критерии подобия. Это свойство подобных систем и составляет основу моделирования.

П редположим, что для описания изучаемых явлений употребляются r основных независимых единиц измерения A₁, А₂,..., A_r (например, в абсолютных системах единиц основными являются единицы длины L, массы М и времени T). Производные единицы измерения имеют вид: . Их размерность  характеризуется числовыми показателями p₁, p₂,..., p_r. Каждая величина Х размерности [Х] = [Q] представляется в виде: X = xQ, где х — числовое выражение величины Х при выбранной системе основных величин A₁, А₂,..., A_r. Пусть изучается класс явлений S, каждое из которых определяется заданием определённых значений системы величин {Y_a}. Два таких явления S ⁽¹⁾ и S ⁽²⁾ называются подобными, если значения величин Y_a⁽²⁾, характеризующие явление S ⁽²⁾ получаются из значений соответствующих величин Y_a⁽¹⁾, характеризующих явление S ⁽¹⁾ по формулам:

г де коэффициент подобия k₁, k₂,..., k_r постоянны, а показатели p₁, p₂,..., p_r определяются размерностью.

величин Y_a.

Предположим, что из системы величин {Y_a} выделена некоторая часть, образующая систему {Х_b} определяющих параметров, так что числовое значение y_z любой величины Y_a является функцией Y_a= f_a{x_b} числовых значений x_b величин X_b и вид функциональных зависимостей f_a остаётся одним и тем же при любом выборе основных единиц измерения A₁, A₂,..., A_r. В этом предположении основной принцип П. т. может быть сформулирован следующим образом. Для подобия явлений S ⁽¹⁾ и S ⁽²⁾ необходимо и достаточно, чтобы значения любой безразмерной комбинации

,     (1)

определяющих параметров в явлениях S ⁽¹⁾ и S ⁽²⁾ были равны: k ⁽¹⁾= k ⁽²⁾.

Каждое безразмерное выражение k вида (1) называется коэффициентом подобия. Очевидно, что при таком определении критериев подобия в их число попадают все безразмерные определяющие параметры и все отношения вида:

,     (2)

где  и  — определяющие параметры одной и той же размерности.

Разница между критерием и числом подобия, по Лойцянскому:

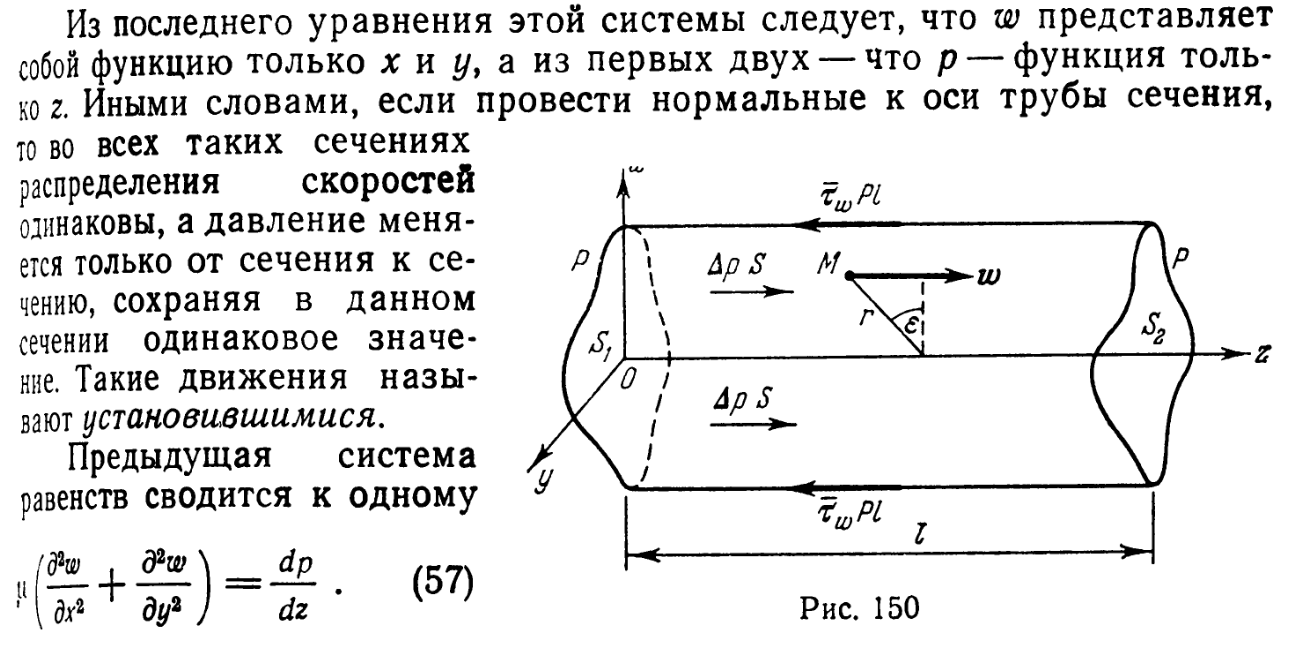
8. Ламинарное движение несжимаемой вязкой жидкости в цилиндрических трубах.

9. Современные представления о ламинаризации (прямом и обратном переходах) при движении вязких сред.

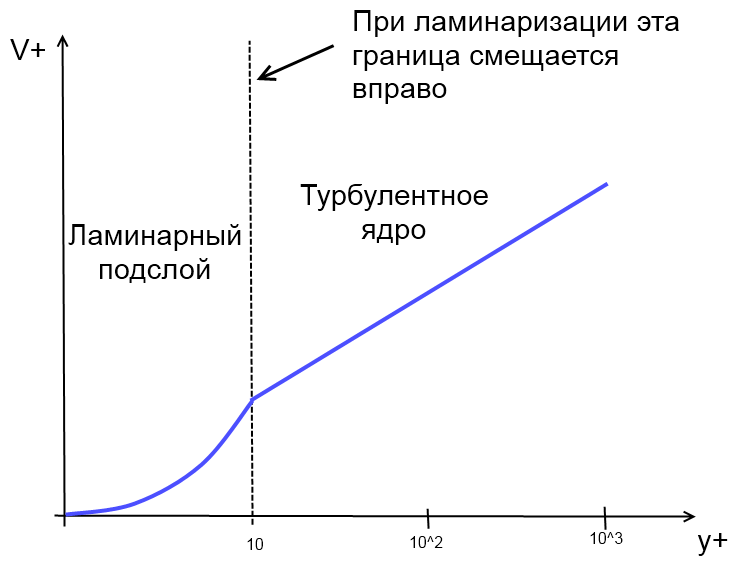
Ламинаризация - неполное подавление возможных пульсационных процессов, связанных с турбулентным переносом тепла, массы, импульса; переход от турбулентного движения к ламинарному.

Реламинаризация - полный переход от турбулентного движения к ламинарному за счет эффектов, связанных с пространственной деформацией движущихся элементов объема. Реламинаризация - локальное явления, и не исключает повторного перехода от ламинарного движения к турбулентному при изменении внешних факторов.

Ранее, переход от ламинарного режима течения к турбулентному и обратно, в цилиндрических каналах, связывали со значением числа Рейнольдса в промежутке от 2200 до 4000. Этот подход основывался на гипотезе о зависимости характеристик течения лишь от «крупномасштабных» параметров средней скорости, диаметра канала и вязкости среды. Однако многочисленные современные экспериментальные данные показывают, что число Рейнольдса не всегда может адекватно предсказать переходные процессы, в особенности в потоках многофазных, многокомпонентных систем, а также в каналах со сложной геометрией. Современный подход к явлению ламинаризации предлагает использовать критерий Кейса:

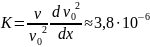-выше этого значения происходит ламинаризация течения.V0 - среднемассовая скорость.

Для корректного изучения всех особенностей ламинаризации, необходимо анализировать локальную структуру течения. Современные представления связаны с учетом механизма вырождения турбулентности, обусловленной пульсациями поля скорости - т.е. увеличением диссипативных процессов в течениях развитого профиля.

Полная ламинаризация - это переход от степенного закона распределения скоростей вида: к параболическому профилю вида:

10. Понятие о динамическом, температурном и диффузионном пограничных слоях при движении вязких неизотермических смесей в трубопроводах.

11. Понятие о методах решения сеточных уравнений (прямые и итерационные методы: Якоби и Гаусса-Зейделя).

Методы решения систем линейных алгебраических уравнений делятся на две группы – прямые и итерационные. Прямые методы используют определенные соотношения (формулы) для вычисления неизвестных. При этом решение получается после выполнения заранее известного количества арифметических операций. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса систем линейных уравнений.

В тоже время прямые методы имеют и ряд недостатков. Как правило, они требуют хранения в оперативной памяти сразу всей матрицы, и при больших значениях n расходуется много места в памяти компьютера. Кроме этого более существенным недостатком прямых методов является накапливание погрешностей в процессе решения, поскольку вычисления на любом этапе используют результаты предыдущих операций.

Прямые методы решения линейных систем иногда называют точными, поскольку решение выражается в виде точных формул через коэффициенты системы. Однако точное решение может быть получено лишь при точном выполнении вычислений (и, разумеется, при точных коэффициентах системы). На практике же при использовании компьютеров вычисления проводятся с погрешностями. Поэтому неизбежны погрешности и в окончательных результатах, вызванные погрешностями вычислений (например, погрешностью округления).

Итерационные методы – это методы последовательных приближений. В них необходимо задать некоторое приближенное решение – начальное приближение, после чего с помощью заданного алгоритма проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводят до тех пор, пока не будет получено решение с заданной точностью.

Важное достоинство итерационных методов состоит в том, что погрешности окончательных результатов не накапливаются, поскольку точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений.

К прямым методам относят методы Гаусса, Крамера, Метод обратных матриц. К итерационным – метод Якоби, метод Гаусса-Зейделя.

Итерационные методы:

. (3.20)

 

Как и в предыдущем параграфе, будем считать, что решение (3.20) существует и единственно.

Различные варианты метода простых итераций связаны с переходом от системы (3.20) к эквивалентной системе

 

. (3.21)

Метод итераций Якоби. Самый простой способ приведения системы (3.20) к виду (3.21) состоит в записи в явном виде неизвестного из первого уравнения, из второго и т.д. Метод итераций в такой реализации называется методом Якоби.

Проиллюстрируем сначала этот метод на примере системы трех уравнений:

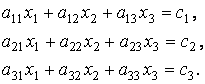(3.26)

 

Предположим, что диагональные элементы , и отличны от нуля. Выразим неизвестные , и соответственно из первого, второго и третьего уравнений системы (3.26):

 

(3.27)

 

Тем самым, мы получили систему уравнений, записанную в виде (3.21), причем матрица В и вектор g имеют здесь следующий вид:

 

, . (3.28)

 

С учетом выражений (3.27) построим итерационный процесс метода Якоби, в котором приближение с номером вычисляется на основе приближения с номером k следующим образом:

 

(3.29)

 

В качестве вектора начальных приближений можно взять нулевой вектор или вектор g, т.е.

 

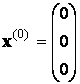или . (3.30)

 

Итерационный процесс (3.29) продолжается до тех пор, пока не выполнится одно из условий (3.24), (3.25).

Рассмотренный метод легко обобщается на систему из n уравнений. Элементы матрицы В и вектора g будут определятся в этом случае следующим образом

 

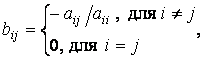
, . (3.31)

 

А система (3.29) принимает вид

 

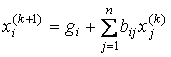, . (3.32)

 

Для сходимости метода Якоби достаточно, чтобы для исходной матрицы А имело бы место диагональное преобладание, т.е. чтобы коэффициенты исходного уравнения удовлетворяли условиям

 

для всех i.

Выполнение этого условия гарантирует, что хотя бы одна из норм матрицы В, элементы которой вычисляются по формуле (3.31), окажется при этом меньше единицы, т.е. будет выполнено общее условие сходимости итерационного процесса (3.23).

Метод Зейделя. Этот метод отличается от метода Якоби только тем, что при вычислении -го приближения i-й компоненты вектора х используются уже вычисленные -е приближения предыдущих (1-й, 2-й, …, -й) компонент вектора х.

Для системы (3.27) итерационный процесс Зейделя будет иметь следующий вид:

 

(3.33)

 

Если ввести нижнюю и верхнюю треугольные матрицы

 

и ,

 

то система (3.33) может быть компактно записана в матричном виде

 

. (3.34)

 

Здесь g – вектор, определенный выше выражением (3.31)

Итерационный процесс (3.26) непосредственно обобщается на систему n уравнений, при этом элементы матриц и определяются следующим образом

 

, .

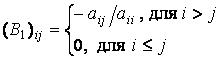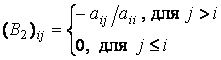. (3.35)

 

При программной реализации метода Зейделя его алгоритм можно организовать таким образом, что необходимость в введении двух треугольных матриц отпадает, и расчет ведется с одной матрицей В, элементы которой вычисляются по формуле (3.31). Опишем этот алгоритм:

 

1.     Ввод n, , , 

2.     Для i от 1 до n :

2.1.Для j от 1 до n :

2.1.1.   Если , тогда , иначе

2.2. ;

3.     Для i от 1 до n :

4.     Для i от 1 до n :

4.1.

4.2.Для j от 1 до n :

4.3.

5.     Если , тогда перейти к шагу 3

6.     Вывод

 

Поясним смысл некоторых переменных и шагов алгоритма. На первом шаге организуется ввод элементов матрицы А, вектора с и заданной точности . На втором шаге вычисляются элементы матрицы В, вектора g, а также задается вектор начальных приближений x, в качестве которого берется вектор g. На третьем шаге запоминаются текущие значения элементов вектора x в векторе y, его смысл – хранить значения неизвестных до выполнения очередной итерации с тем, чтобы можно было сравнивать их значения на -й и k-й итерациях. На четвертом шаге совершается одна итерации в соответствии с формулой (3.34). На пятом шаге происходит сравнение значение элементов вектора x на двух последовательных итерациях и, если вектора отличаются больше чем на величину  (вычисления модуля разности векторов выполняется по формуле (3.24)), то шаги, начиная с третьего, повторяются еще раз.

Доказано, что метод Зейделя гарантировано сходится, если:

–       для матрицы А выполнено условие диагонального преобладания

или

–       матрица А является симметричной и положительно определенной, т.е. такой что и .

Системы уравнений с симметричными и положительно определенными матрицами называются нормальными системами. Для приведения любой системы к нормальному виду, достаточно выполнить простые преобразования, а именно умножить левую и правую части системы слева на транспонированную матрицу¹[2] :

 

.

 

Если ввести новую матрицу и вектор , то получившаяся эквивалентная система

 

 

будет обладать необходимыми свойствами нормальной системы.

Для систем с нормальной матрицей метод Зейделя сходится примерно в два раза быстрее метода Якоби. Однако в общем случае возможны ситуации, когда метод Якоби сходится, а метод Зейделя или сходится медленнее, или не сходится вовсе. Возможны также и противоположные ситуации.

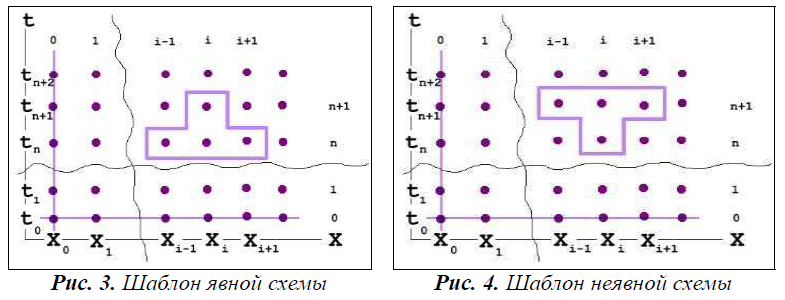
12. Решение уравнения диффузии (явная и неявная схемы). В ОТВЕТЕ ВМЕСТО U(скорость) НУЖНО ПИСАТЬ С(концентрация)! Тогда это будет нормальное уравнение диффузии.

13. Понятие об обобщенных законах теплопроводности Фурье.

14. Понятие о средних, среднемассовых и среднеэнергетических параметрах в исследовании гидродинамики и тепломассообмена в углеводородных смесях.

Среднее значение функции — это некоторое число, заключённое между наименьшим и наибольшим её значениями. Если говорить о параметрах гидродинамики, то они в абсолютном большинстве обладают непрерывным распределением. Вследствие этого под средним значением функции на отрезке обычно понимают величину

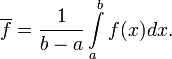
Среднемассовое значение функции - также некоторое число, заключённое между наименьшим и наибольшим её значениями. В исследованиях гидродинамики применяется для анализа параметров многокомпонентных углеводородных смесей. Вследствие того, что компоненты находятся не в равном количественном соотношении друг с другом (одного больше, другого меньше), необходим учет вклада каждого из компонент в искомую величину в соответствие с его массой (плотностью). В связи с этим в расчете участвует «весовой коэффициент» - плотность той фазы, которой принадлежит вклад в искомую величину. Например, выражение для среднемассовой скорости выглядит так:

где pm - плотность смеси, ai - объемная доля компонента, pi - плотность компонента, vi - скорость компонента.

Среднеэнергетическое значение функции - аналогично среднемассовой, но в качестве весового параметра используется удельная кинетическая энергия фазы.

15. Понятие о принципе Кюри и скрещивающих явлениях в многокомпонентных неизотермических вязких средах (эффекты концентрационной диффузии, баро-, дино-, термодиффузии, диффузионной теплопроводности в смесях).

В некоторых случаях изменения в потоках тепла и массы, вызванные эффектами, не связанными напрямую с теплопроводностью и молекулярной диффузией, могут быть соизмеримы с вкладом эффектов, описываемых законами Фурье и Фика. В этих случаях необходим учет «скрещивающихся» эффектов», описывающих влияние массообмена на теплообмен, и наоборот.

Если температура смеси переменна, то возникает так называемая термическая диффузия (эффект Соре). Из кинетической теории газов следует, что если массы молекул двух компонентов различны, то за счет термодиффузии более тяжелые молекулы большей частью стремятся перейти в холодные области; если же массы молекул одинаковы, то в холодные области стремятся перейти более крупные молекулы. При определенных условиях направление термодиффузии может изменяться. Например, в ионизированном газе более тяжелые молекулы (или ионы) будут стремиться перейти в более теплые области. Термодиффузия приводит к образованию градиента концентрации. Этому препятствует процесс концентрационной диффузии, стремящейся выровнять состав. В результате с течением времени может установиться стационарное состояние, при котором уравновесятся противоположные влияния термодиффузии и концентрационной диффузии.

Следствием молекулярного диффузионного переноса тепла является так называемый диффузионный термоэффект (эффект Дюфо), представляющий собой возникновение разности температур в результате диффузионного перемещения двух газов, первоначально имевших одинаковую температуру.   Диффузионный термоэффект — явление, обратное термодиффузии. При стационарном диффузионном смешении, например, водорода и азота возникает разность температур порядка нескольких градусов. Возникающий при диффузионном термоэффекте градиент температуры имеет такое направление, что термодиффузия, которая является его результатом, противоположна диффузии, благодаря которой появился этот градиент. Если в смеси имеет место градиент полного давления, то может возникнуть диффузия за счет неоднородности давления. Этот вид диффузии называют бародиффузией. При бародиффузии тяжелые молекулы стремятся перейти в область повышенного, а легкие — в область пониженного давления. Как и термодиффузия, бародиффузия сопровождается и обычным переносом массы, вызванным разностью концентрации. Динодиффузия (диффузия под действием внешних сил) наблюдается, например, в газе, вращающемся вокруг оси; в этом случае тяжелые молекулы стремятся перейти в области, наиболее удаленные от центра. С учетом концентрационной диффузии, термодиффузии и бародиффузии плотность потока массы -го компонента за счет молекулярного переноса описывается следующим уравнением:

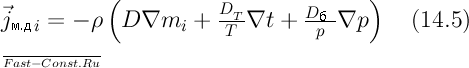
Математически, условие возникновения скрещивающих эффектов объясняют соотношением Онзагера и принципом Кюри. Соотношение Онзагера записывается следующим образом:

, где L - феноменологические коэффициенты, Х - движущие силы. То есть поток определяется суммой отдельно действующих движущих сил (пример: движущая сила потока тепла - градиент температуры. Тепло переходит от более теплого тела к более холодному), помноженных на константы (например, на теплопроводность в примере с теплом).

Принцип Кюри утверждает, что скрещивающие эффекты возможны только в тех случаях и между теми потоками величин, движущие силы которых отличаются значениями рангов своих тензоров на четную величину, либо на ноль. То есть либо это тензоры одного порядка, либо их порядок отличается на 2. Пример - эффекты диффузии и теплопроводности. В обоих эффектах движущая сила - это градиент величины - градиент концентрации для диффузии, и градиент температуры для теплопроводности. Градиент - это вектор, то есть тензор 1-го ранга. Разница между рангами тензоров двух движущих сил этих эффектов: 1-1=0. То есть выполняется принцип Кюри и данные потоки величин могут влиять друг на друга, что и наблюдается в природе.