
- •1. Сформулируйте определение числа и вектора Фробениуса неотрицательной матрицы. Сформулируйте теорему Фробениуса-Перрона.
- •2. Сформулируйте 1-ый критерий продуктивности.
- •4.Сформулируйте определение запаса продуктивности неотрицательной матрицы. Выведите формулу для вычисления запаса продуктивности через число Фробениуса.
- •6. Приведите примеры задач линейного программирования на минимум ( задача о диете) и на максимум (задача об использовании ресурсов): текстовую формулировку и математическую постановку задачи.
- •7. Приведите общую постановку злп. Дайте определения следующим терминам: целевая функция, допустимое множество задачи, оптимальное решение, оптимальное множество.
7. Приведите общую постановку злп. Дайте определения следующим терминам: целевая функция, допустимое множество задачи, оптимальное решение, оптимальное множество.
Если целевая функция и система ограничений линейны, т. е. каждая из них имеет вид a1x1 + a2x2 + … +anxn +b, то задача математического программирования называется задачей линейного программирования (ЗЛП).
На практике часто встречаются такие ситуации, когда достичь какого-то результата можно не одним, а несколькими различными способами. Когда решений много, ищется наилучшее. Математически это сводится к задаче: найти max (min) f(x) при условии, что переменная x пробегает некоторое заранее известное множество X. f(x) → max(min), x ϵ Х.
Такая задача называется задачей оптимизации. Множество X называется допустимым множеством данной задачи, а функция f(x) – целевой функцией. Следует находить не только само значение max (min) f, но и точку или точки, если их несколько, в которых это значение достигается. Такие точки называются оптимальными решениями. Множество всех оптимальных решений называют оптимальным множеством и обозначают X*.
8. Что такое стандартная форма задачи линейного программирования? Что такое каноническая форма задачи линейного программирования? Приведите пример задачи, форма которой не является ни канонической, ни стандартной. Приведите эту задачу к канонической и стандартной формам.
Каноническая форма ЗЛП, помимо нетривиальных ограничений, включает в себя только уравнения (пример транспортная ЗЛП)
Стандартная форма ЗЛП состоит только из неравенств, включая тривиальные ограничения.
Пример 1. Привести данную ЗЛП к каноническому виду.
 2х1
+ х3>=40
2х1
+ х3
– x4=40
2х1
+ х3>=40
2х1
+ х3
– x4=40
3х2 + х3 = 30 f=20х1 + 5х2 + 30х3 -> min 3х2 + х3 = 30
Хi >=0 Хi >=0
Пример 2. Привести заданную ЗЛП к стандартному виду.
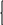
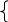 2х1
+ х3>=40
2х1
+ х3
>=40
2х1
+ х3>=40
2х1
+ х3
>=40
3х2 + х3 - x4 = 30 f=20х1 + 5х2 + 30х3 -> min 3х2 + х3 - 30>= 0
Хi >=0 Хi >=0
9. Опираясь на алгоритм графического метода, постройте две задачи линейного программирования с одной и той же целевой функцией f(x1, x2)=x1+x2, в одной из которых существует единственная точка максимума, а в другой – бесконечное множество точек минимума. Допустимую область задачи изобразите на чертеже и задайте системой неравенств.
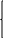
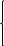 1)
f(x1,
x2)=x1+x2
-> max 2) f(x1,
x2)=x1+x2
-> min
1)
f(x1,
x2)=x1+x2
-> max 2) f(x1,
x2)=x1+x2
-> min
x1+x2≤6 (1) x1+x2≥3 (1)
2x1+x2≤8 (2) x1+x2≤6 (2)
x1≥0 x2≥0 2x1+x2≤8(3)
 x1≥0
x2≥0
x1≥0
x2≥0
y

Линия
уровня совпадает с прямой (1). Из этого
следует, что существует множество точек
минимума, принадлежащих прямой (1).
Точка максимума единственная – с координатами (2;4). Координаты мы получили, приравняв (1) и (2).
10. Опираясь на алгоритм графического метода, постройте две задачи линейного программирования с одной и той же целевой функцией f(x1, x2)=x1+x2, в одной из которых существует единственная точка минимума, а в другой – бесконечное множество точек максимума. Допустимую область задачи изобразите на чертеже и задайте системой неравенств.
x1+x2≤6 (1) 2x1+x2≤8 (2) x1≥0 x2≥0
Точка минимума единственная и совпадает с началом координат, т.е. имеет координаты (0;0)
11. Опираясь на алгоритм графического метода, постройте две задачи линейного программирования с одной и той же целевой функцией f(x1, x2)=x1+x2, в одной из которых существует единственная точка минимума, а в другой целевая функция не ограничена сверху. Допустимую область задачи изобразите на чертеже и задайте системой неравенств.
12. Опираясь на алгоритм графического метода, постройте две задачи линейного программирования с одной и той же целевой функцией f(x1,x2) = x1 + x2, в одной из которых существует единственная точка максимума, а в другой целевая функция не ограничена снизу. Допустимую область задачи изобразите на чертеже и задайте системой неравенств.
x1 + 2x2 ≤ 16 2x1 + x2 ≤ 14 3x1 + 3x2 ≥ 6 x1, x2 ≥ 0
Б) f(x1,x2) = x1 + x2 max x2 ≤ 2 x1 + x2 ≤ 15 x1 ≥ 0
А) f(x1,x2) = x1 + x2 min x1 + x2 ≥ 1 0 ≤ x2 ≤ 3 0 ≤ x1 ≤ 4
x1 - x2 ≥ -3 x1 - x2 ≤ -3 x1, x2 ≥ 0
Функция не ограничена сверху
x1 + x2 ≥ 5 x1, x2 ≥ 0
Задача имеет бесконечное множество точек максимума
x2 ≤ 2 x1 + x2 ≤ 15 x1 ≥ 0 Функция не ограничена снизу
16. Рассматривается задача линейного программирования, в которой целевая функция исследуется на минимум. Является ли симплекс-таблица окончательной? Рассматривается задача линейного программирования, в которой целевая функция исследуется на минимум. Является ли симплекс-таблица окончательной?
Не окончательная, т.к. в последней строке есть положительные элементы. 5 -2 1 0 3 -13/3 0 1 2/3 1/3 -1 3 0 1 4 -> -1/3 1 0 1/3 4/3 -2 3 0 0 10 -1 0 0 -1 6 Ответ: fmin=6, единственное решение.
17. Рассматривается задача линейного программирования, в которой целевая функция исследуется на минимум. Является ли симплекс-таблица окончательной?
Не окончательна. Так как в целевой функции (последняя строка) есть положительный элемент =3. В столбце с этим положительным элементом есть положительное число (во второй строке) = 3. Ее и возьмем за разрешающий элемент:
F(0,4/3,17/3,0)=6 – окончательное решение. Так как последняя строка не содержит положительных элементов, а в силу того, что функция исследуется на минимум, то план нас устраивает.
18. Рассматривается задача линейного программирования, в которой целевая функция исследуется на минимум. Является ли симплекс-таблица окончательной?
Окончательная, т.к. в последней строке не положительных элементов. Ответ: fmin=10, единственность решения.
19. Рассматривается задача линейного программирования, в которой целевая функция исследуется на максимум. Является ли симплекс-таблица окончательной?
Окончательная, т.к. в последней строке нет отрицательных элементов. Ответ: fmax=10, единственность решения.
20. Рассматривается задача линейного программирования, в которой целевая функция исследуется на максимум. Является ли симплекс-таблица окончательной?
fmax=-fmin Т.к в последней строке есть положительный элемент, а в соответствующем ему столбце есть положительный элемент, то решение может быть улучшено. Выполняем шаг симплекс метода
Т.к. в последней строке у нет отрицательных элементов, то для нашей функции, исследуемой на максимум, таблица является окончательной f max (3/5,0,0,23/5) = 11 + 1/5 = 56/5
21. Рассматривается задача линейного программирования, в которой целевая функция исследуется на максимум. Является ли симплекс-таблица окончательной?
maxF=-minF В последней строке есть положительный элемент, но в соответствующем ему столбце (не учитывая строку F) нет положительных элементов, следовательно maxf = -minf=беск
22. Рассматривается задача линейного программирования, в которой целевая функция исследуется на максимум. Является ли симплекс-таблица окончательной?
Данная таблица – окончательная, потому что в строке оценок задачи максимум отсутствуют отрицательные оценки. Решение рассматриваемой задачи линейного программирования имеет вид fmax=f(0;0;3;4)=10. Поскольку нулевая оценка присутствует в небазисном столбце (x1), решение не единственно.
Можно сформулировать правила получения двойственной задачи из задачи исходной. 1. Если в исходной задаче ищется максимум целевой функции, то в двойственной ей - минимум. 2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи. 3. В исходной ЗЛП все функциональные ограничения - неравенства вида “≤”, а в задаче, двойственной ей, - неравенства вида “≥”. 4. Коэффициенты при переменных в системах ограничений взаимно двойственных задач описываются матрицами, транспонированными относительно друг друга. 5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой. 6. Условие неотрицательности переменных сохраняется в обеих задачах.
24. . Сформулируйте и докажите основное неравенство для взаимно двойственных задач линейного программирования. Сформулируйте достаточный признак оптимальности. Основное нер-во двойственности. Пусть Х – какое-нибудь допустимое решение задачи I, а У – какое-нибудь допустимое решение задачи II. Тогда справедливо неравенство f(x)<φ(Y) Доказательство: Имеем AX<B, откуда следует (АХ)T<BT или XTAT<BT. Умножим обе части этого неравенства справа на матрицу У>0=0, получим (XTAT)Y<BTY или, в ввиду ассоциативности умножения матриц, XT(ATY)<BTY=φ(Y) (I) Аналогично имеем ATY>С; умножив обе части слева на матрицу XT>0, будем иметь XT(ATY)>XTC=f(X) (II) Соединяя два полученных неравенства I и II, можем записать F(X)<XTATY< φ(Y), откуда и следует основное неравенство f(X)< φ(Y).
25. Сформулируйте первую и вторую теоремы двойственности. Докажите вторую теорему двойственности. Первая теорема двойственности. Если исходная задача имеет оптимальное решение, то и двойственная ей также имеет оптимальное решение. При этом оптимальные значения целевых функций обеих задач равны: fmax=gmin. Вторая теорема двойственности. Если хотя бы одно оптимальное решение одной из двойственных задач обращает i-е ограничение этой задачи в строгое неравенство, то i-я компонента (т.е. xi или ui) каждого оптимального решения второй двойственной задачи равна нулю. Если же i -я компонента хотя бы одного оптимального решения одной из двойственных задач положительна, то каждое оптимальное решение другой двойственной задачи обращает i -е ограничение в строгое равенство. Доказательство:
Пусть
Умножим
(3), соответственно, на
Из основной теоремы двойственности следует
И с учетом (4) получаем:
Первое
из этих выражений можем переписать в
виде
и
так как все
и
выражения в скобках неотрицательны,
то опуская å, получим:
Аналогично
получим:
26. Приведите пример постановки транспортной задачи. Что такое оптимальный план перевозок? Что такое транспортная задача с правильным балансом? Сформулируйте критерий разрешимости транспортной задачи. 1) Классическая постановка транспортной задачи общего вида. Имеется m пунктов отправления («поставщиков») и n пунктов потребления («потребителей») некоторого одинакового товара. Для каждого пункта определены: ai – объемы производства i -го поставщика, i = 1, …, m; вj – спрос j-го потребителя, j= 1,…,n; сij – стоимость перевозки одной единицы продукции из пункта Ai– i-го поставщика, в пункт Вj – j-го потребителя. Требуется найти план перевозок, при котором бы полностью удовлетворялся спрос всех потребителей, при этом хватало бы запасов поставщиков и суммарные транспортные расходы были бы минимальными. 2) Оптимальный план перевозок - такой план перевозок, который определяет минимальную суммарную стоимость транспортировки, не превышая объем производства каждого из поставщиков и полностью покрывая потребности каждого из потребителей. 3) Транспортная задача с правильным балансом. Теорема:
если допустимое решение Х=(хij)*(i= Общее
кол-во товара у поставщиков:
Общая
потребность в товаре в пунктах
назначения:
4) Критерий разрешимости транспортной задачи: Транспортная задача разрешима только, если она имеет правильный баланс.
28 . Опишите метод потенциалов. Сформулируйте определения следующих понятий: свободная клетка, занятая клетка, оценка свободной клетки, цикл, перестановка по циклу. В чем состоит условие оптимальности опорного плана?
Метод потенциалов основан на следующей теореме. Если
допустимое решение Х=( xij)
(i= ui+ vj=сij, если xij>0, ui+ vj<либо =сij, если xij=0. Равенства ui+ vj=сij при xij>0 используются для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных ui,i= и vj, j= . Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n-1. Так как число неизвестных системы на единицу больше числа уравнений, то одно из них можно задать произвольно ( как правило, его берут нулевым), а остальные найти из системы. Неравенства
ui+
vj<либо =сij
при
xij=0
используются для проверки оптимального
опорного решения. Эти неравенства
удобно записать в виде
Числа ij по-прежнему будем называть оценками свободных клеток таблицы, не входящих в базис опорного решения. В это случае признак оптимальности можно сформулировать так же, как в симплекс-методе (для задачи на минимум): опорное решение является оптимальным, если для всех клеток таблицы оценки неположительные.
Оценка свободной клетки – (см. метод потенциалов) Цикл – такая последовательность клеток транспортной таблицы (i1,j1), (i1,j2), (i2,j2),…(ik,j1), в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или столбце. (?)Перестановка по циклу - (сдвиг по циклу на величину t)- увеличение объемов во всех нечетных клетках цикла, отмеченных знаком «+», на t и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком «-», на t.
Оптимальный план должен определять минимальную суммарную стоимость транспортировки, не превышая объем производства каждого из поставщиков и полностью покрывая потребности каждого из потребителей. Оптимальный
план перевозки соответствует минимуму
линейной целевой функции f(X)=
27. Опишите метод минимального тарифа построения начального опорного плана транспортной задачи.
Начальный опорный план находят, заполняя не более чем m+n-1 клеток (по числу базисных переменных). Любое допустимое решение транспортной задачи можно записать в транспортную таблицу. Клетки транспортной таблицы, в которых находятся отличные от нуля (или базисные нулевые) перевозки, называются занятыми, остальные свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку xij, т.е. стоящая в i-строке и j- столбце, имеет номер (i,j). Каждой клетке с номером (i,j) соответствует переменная xij. Выбор заполняемых клеток производят, ориентируясь на тарифы перевозок, а именно: на каждом шаге выбирают какую-нибудь клетку (i,j), отвечающую минимальному тарифу и помещают в нее максимально возможную перевозку xij. После чего удаляют либо столбец, либо строку в зависимости от соотношения xij=bj или xij=ai.
|
2) f(x1, x2)=x1+x2 -> max x1+x2≤6 (1) x1≥0 x2≥0
Линия уровня совпадает с единственной прямой (1), поэтому существует множество точек максимума.
|

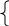
 1)
f(x1,
x2)=x1+x2
-> min
1)
f(x1,
x2)=x1+x2
-> min

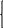 1)
f(x1,
x2)=x1+x2
--> min
1)
f(x1,
x2)=x1+x2
--> min
 2)
f(x1,
x2)=x1+x2
--> max
2)
f(x1,
x2)=x1+x2
--> max
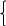
 А)
f(x1,x2)
= x1
+ x2
max
А)
f(x1,x2)
= x1
+ x2
max
 13.
Опираясь на алгоритм графического
метода, постройте две задачи линейного
программирования с одной и той же
целевой функцией f(x1,x2)
= x1
+ x2,
в
одной из которых существует бесконечное
множество точек минимума, а в другой
целевая функция не ограничена сверху.
Допустимую область задачи изобразите
на чертеже и задайте системой неравенств.
13.
Опираясь на алгоритм графического
метода, постройте две задачи линейного
программирования с одной и той же
целевой функцией f(x1,x2)
= x1
+ x2,
в
одной из которых существует бесконечное
множество точек минимума, а в другой
целевая функция не ограничена сверху.
Допустимую область задачи изобразите
на чертеже и задайте системой неравенств.
 Задача
имеет бесконечное множество точек
минимума
Задача
имеет бесконечное множество точек
минимума
 Б)
f(x1,x2)
= x1
+ x2
max
Б)
f(x1,x2)
= x1
+ x2
max 14.Опираясь
на алгоритм графического метода,
постройте две задачи линейного
программирования с одной и той же
целевой функцией f(x1,x2)
= x1
+ x2,
в
одной из которых существует бесконечное
множество точек максимума, а в другой
целевая функция не ограничена снизу.
Допустимую область задачи изобразите
на чертеже и задайте системой неравенств.
14.Опираясь
на алгоритм графического метода,
постройте две задачи линейного
программирования с одной и той же
целевой функцией f(x1,x2)
= x1
+ x2,
в
одной из которых существует бесконечное
множество точек максимума, а в другой
целевая функция не ограничена снизу.
Допустимую область задачи изобразите
на чертеже и задайте системой неравенств.
 А)
f(x1,x2)
= x1
+ x2
max
А)
f(x1,x2)
= x1
+ x2
max
 Б) f(x1,x2)
= x1
+ x2
max
Б) f(x1,x2)
= x1
+ x2
max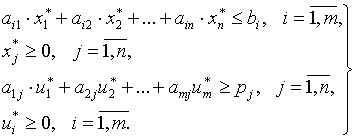 .
(3)
.
(3)
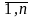 ,
j=
,
j=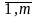 )
транспортной задачи является
оптимальным, то существует потенциалы
поставщиков ui
(i=
)
и потребителей vj(j=
).
Удовлетворяющее условиям: 1) ui+vj=cij,
если xij>0;
2) ui+vj
≤cij,
если xij=0.
)
транспортной задачи является
оптимальным, то существует потенциалы
поставщиков ui
(i=
)
и потребителей vj(j=
).
Удовлетворяющее условиям: 1) ui+vj=cij,
если xij>0;
2) ui+vj
≤cij,
если xij=0.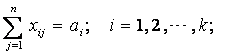
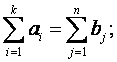 то
такая задача называется задачей с
правильным
балансом,
а ее модель — закрытой.
то
такая задача называется задачей с
правильным
балансом,
а ее модель — закрытой.
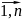 ,
j=
,
j= )
транспортной задачи является
оптимальным, то существуют потенциалы
поставщиков ui(i=
)
и потребителей vj
(j=
),
удовлетворяющие условиям:
)
транспортной задачи является
оптимальным, то существуют потенциалы
поставщиков ui(i=
)
и потребителей vj
(j=
),
удовлетворяющие условиям: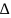 ij=ui+vj-cij
при
xij=0.
ij=ui+vj-cij
при
xij=0.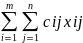
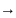 min
при ограничениях на потребление и
поставку
min
при ограничениях на потребление и
поставку