6. Метод интегрирования по частям

Пусть u = u(x), v = v(x) – дифференцируемы на D

d(u•v) = du•v + u•dv  ∫ d(u•v) = ∫du•v + ∫u•dv  u•v = ∫v•du + ∫u•dv 

∫u•dv = u•v - ∫v•du – формула интегрирования по частям

Применение данной формулы:

1. P_n (x)•φ(x)dx; P_n (x) – многочлен n-ой степени

а ) φ(x) = sin ax u = P_n (x); dv = φ(x)dx

cos ax

e^Kx

b) φ(x) = обратные тригонометрические функции u = φ(x); dv = P_n (x)dx

log_ax

2 . e^kx•sin ax dx в этом случае любой из множителей можно принять

e^kx•cos ax dx за u

7. Определение определенного интеграла Римана.

Пусть f(x) определена и ограничена на [a,b]. Если Ǝ конечный 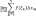не зависящий от выбора x₀, x₁..x_n и ξ_1,ξ₂…ξ_n то эта величина называется определенным интегралом и обозначается; лямбда = max(k-тое)дельта x(n-ное) – мелкость T

8. Достаточное условие интегрируемости.

Для того, чтобы ф-ция у=f(x), определенная и ограниченная на отрезке [a,b], была интегрируемой на этом отрезке, необходимо и достаточно, чтобы для любого ε›0 существовало разбиение T, такое что S_t-s_t< ε

9. Геометрический смысл определенного интеграла.

Определенный интеграл равен площади криволинейной трапеции, ограниченной вертикальными прямыми х=а, х=b при a<b, осью Ох и графиком неотрицательной и непрерывной ф-ции у=f(x),

1. f(x)>=0 на [a,b](рисунок) S= ; 2. f(x)<=0 на [a,b](рисунок) S=-…; 3. f(x)мен знак на [a,b]S=S1-S2+S3.

10. Свойства определенного интеграла.

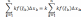1)f(x)- интегрируема на [a,b] k≠0, k – const. Док-во: T, ξ_k € [x _k-1,x_k], 𝛌-maxk ∆x. Тк f-интегрируема, то Ǝ конечный предел

2) g(x), f(x) интегрируема на [a,b] Тогда

Док-во:

Тк ф-ции g(x) и f(x) интегрируемы на [a,b], то с правой стороны Ǝ конечные пределы, значит Ǝ и сумма этих пределов, сумма пределов = пределов суммы (по св-ву предела) след. Ǝ предел слева.

11. Формула Ньютона-Лейбница:

Пусть функция y=f(x) непрерывна на отрезке [a;b] и F(x)- первообразная для f(x). Тогда:

∫(a по b) f(x)dx= F(b)-F(a)=F(x)l(a по b).

Следствие: 1. ∫(a по b) F’(x)dx= F(x)l(a по b)

2.∫(a по b) dF(x)dx= F(x)l(a по b)

12. Формула замены переменной в определенном интеграле:

Пусть функция x=A(t) определена и дифференцируема на промежутке T и X – множество ее значений, на котором определена функция f(x). Тогда если F(x) – первообразная для f(x) на X, то F(A(t))- первообразная для f(A(t))A’(t) на T, т.е. на множестве Т выполняется равенство:

∫f(x)dx│x=A(t) = ∫f(A(t))A’(t)dt

13. Формула интегрирования по частям для определенного интеграла:

Пусть u(x) и v(x) – две дифференцируемые функции на промежутке X. Тогда на Х выполняется формула интегрирования по частям:

∫udv=uv-∫vdu (a по b) Док-во: (uv)’= u’v+uv’.

d(uv)=vdu+udv. uv│(a по b)= ∫(a b)d(uv)= ∫vdu+∫udv(a b). ∫udv(a b)=uv│(a b)- ∫(a b)vdu.

14. Определение несобственного интеграла с бесконечным верхним пределом:

Пусть функция y=f(x) интегрируема на каждом конечном отрезке [a;b] (b>a). Тогда за несобственный интеграл принимают:

∫(a по +∞)f(x)dx= lim b→∞ ∫(а по b)f(x)dx

,когда b стремится к бесконечности. Если сущест конеч предел(выше), то гов, что инт-л сходится; если не сущест – не сходится.

15. Определение несобственного интеграла с бесконечным нижним пределом:

По аналогии с верхним вопросом можно рассмотреть несобственный интеграл с бесконечным нижним пределом, а именно:

∫(b по -∞)f(x)dx= lim a→-∞ ∫(b по a)f(x)dx

16. Определение несобственного интеграла от неограниченной функции на ограниченном промежутке:

Точка x=b-особая для ф-ции f(x), если в любой окр-ти т. x=b ф-ция неогр-на, а на любом пром-ке, леж внутри [a,b]-ф-ция огр-на. Опр: ф-ция интегрируема на [a,x],т. x=b-особая, a<=x<b. Несоб инт-м от неогр ф-ции называется lim ε→0+0 ∫(a по b- ε) f(x)dx:= ∫(a по b) f(x)dx. Если А конечна, то инт-л сх-ся. Если А =+- ∞ или А сущест, то расх-ся. Аналогично, если а – особая точка, то

∫(а по b)f(x)dx= lim ε→0+0 ∫(a+ ε по b)f(x)dx

Если с- един внутр точка, то ∫(a по b)f(x)dx=∫(а по c)f(x)dx + ∫(с по b)f(x)dx.