Основные обозначения и формулы

- объем подгруппы, т.е. число выборочных наблюдений в подгруппе;

- число подгрупп;

- среднее значение в подгруппе;

- среднее значение по всем подгруппам;

- истинное среднее процесса;

- номинал;

- медиана в подгруппе (см. Приложение Ж);

- среднее значение медиан подгрупп;

- размах в подгруппе (разность между максимальным и минимальным значением);

- средний размах;

- выборочное стандартное отклонение в подгруппе (сигма);

- средняя по всем подгруппам сигма;

, - номинальные значения соответствующих величин.

Ниже в таблицах З1 и З2 приведены формулы для построения различных контрольных карт и значения фигурирующих в них коэффициентов. Пояснения к приводимым формулам и входящим в них коэффициентам приведены в нижеследующих разделах.

Таблица З1. Формулы для контрольных карт
Статистика	Стандартные значения не заданы		Стандартные значения заданы
	Центральная линия	UCL и LCL	Центральная линия	UCL и LCL
		или	или
		, 0	или	, 0
		, 0	или	, 0
Индивид. значение			или
Медиана			или

Таблица З2. Значения коэффициентов для построения контрольных карт
n	A	A2	A3	A4	B4	B6	D2	D4	с4	d2(dn)	Dn	e
2	2,121	1,880	2,659	1,88	3,267	2,606	3,686	3,267	0,7979	1,128	0,727	1,000
3	1,732	1,023	1,954	1,19	2,568	2,276	4,358	2,574	0,8886	1,693	0,789	0,743
4	1,500	0,729	1,628	0,80	2,266	2,088	4,696	2,282	0,9213	2,059	0,774	0,838
5	1,342	0,577	1,427	0,69	2,089	1,964	4,918	2,114	0,9400	2,326	0,747	0,697
6	1,225	0,486	1,287	0,55	1,970	1,874	5,078	2,004	0,9515	2,534	0,719	0,776
7	1,134	0,419	1,182	0,51	1,882	1,806	5,204	1,924	0,9594	2,704	0,694	0,679
8	1,061	0,373	1,099	0,43	1,815	1,751	5,306	1,864	0,9650	2,847	0,672	0,743
9	1,000	0,337	1,032	0,41	1,761	1,707	5,393	1,816	0,9693	2,970	0,652	0,669
10	0,949	0,308	0,975	0,36	1,716	1,669	5,469	1,777	0,9727	3,078	0,635	0,723
11	0,905	0,285	0,927	0,35	1,679	1,637	5,535	1,744	0,9754	3,173	0,620	0,663
12	0,866	0,266	0,886	0,32	1,646	1,610	5,594	1,717	0,9776	3,258	0,606	0,709
13	0,832	0,249	0,850	0,31	1,618	1,585	5,647	1,693	0,9794	3,336	0,594	0,659
14	0,802	0,235	0,817	0,28	1,594	1,563	5,696	1,672	0,9810	3,407	0,582	0,699
15	0,775	0,223	0,789	0,28	1,572	1,544	5,741	1,653	0,9823	3,472	0,572	0,656
16	0,750	0,212	0,763	0,25	1,552	1,526	5,782	1,637	0,9835	3,532	0,562	0,692
17	0,728	0,203	0,739	0,25	1,534	1,511	5,820	1,622	0,9845	3,588	0,554	0,653
18	0,707	0,194	0,718	0,23	1,518	1,496	5,856	1,608	0,9854	3,640	0,546	0,686
19	0,688	0,187	0,698	0,23	1,503	1,483	5,891	1,597	0,9862	3,689	0,538	0,651
20	0,671	0,180	0,680	0,22	1,490	1,470	5,921	1,585	0,9869	3,735	0,531	0,681

Карты среднего и выборочного стандартного отклонения ( )

Рассматриваемый метод контроля включает в себя две контрольные карты:

- карта (средних значений) и - карта (среднеквадратичных отклонений)

Рассмотрим их последовательно

Центральная линия для - карты есть:

, если стандартные значения не заданы

номинал, если он задан

Верхняя и нижняя контрольные границы: UCL и LCL

, если стандартная сигма не задана

, если стандартная сигма задана

Здесь:

Эту формулу понять очень легко. Она говорит просто, что нужно взять трех –сигмовые границы и учесть, что сигма среднего для выборки из независимых элементов в раз меньше, чем сигма исходных наблюдений: .

Коэффициенты и выражаются через гамма - функцию:

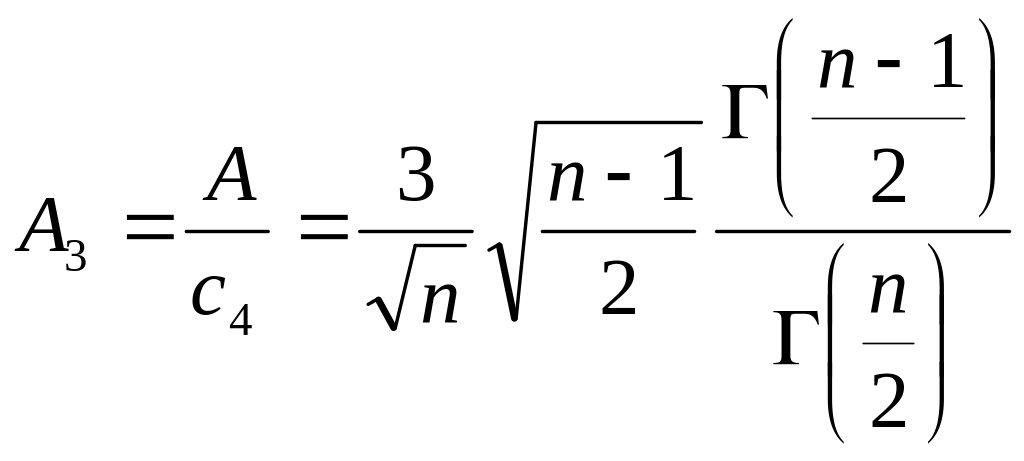
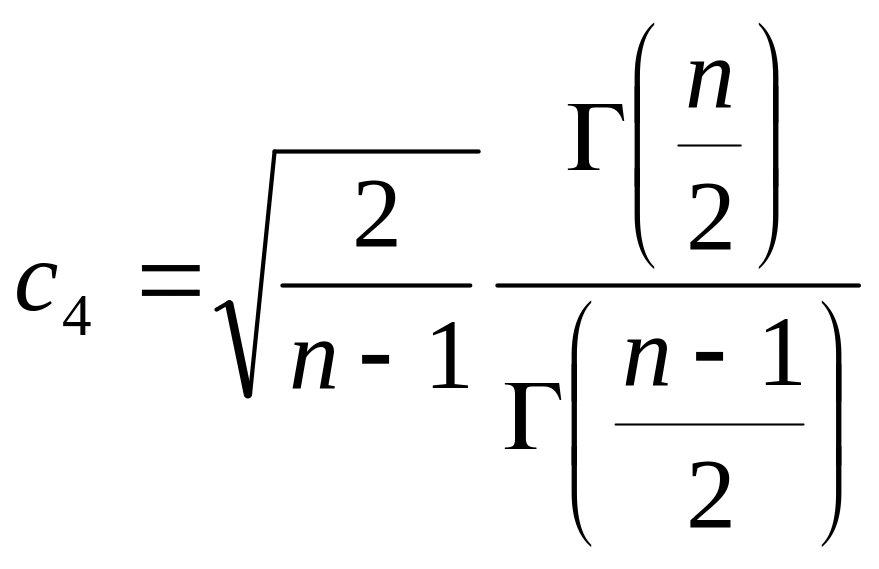
Поясним последние две формулы

Для каждой подгруппы дисперсия вычисляется по обычной формуле (так называемая несмещенная оценка дисперсии)

,

стандартное отклонение в каждой подгруппе есть корень из указанной величины.

Среднее по всем подгруппам есть

Несмещенность оценки дисперсии означает, что математическое ожидание выборочной дисперсии совпадает с истинной дисперсией

В то же время, математическое ожидание выборочного стандартного отклонения отличается от истинного стандартного отклонения некоторым, отличным от единицы коэффициентом :

Поправочный коэффициент , как раз, позволяет уточнить оценку сигмы через выборочное стандартное отклонение по формуле и, таким образом, объяснить отличие коэффициента от .

Рассмотрим теперь - карту (среднеквадратичных отклонений).

Центральная линия (CL):

если стандартная сигма не задана:

если стандартная сигма задана: (эта формула, как раз, показывает, что контролируемым параметром является не сама сигма, а отличающаяся от нее коэффициентом величина , равная квадратному корню из выборочной дисперсии)

Нижняя контрольная граница (LCL) =0.

Указанный выбор соответствует рекомендации отраслевого стандарта [27], хотя, в общем случае, можно устанавливать и ненулевую нижнюю границу на разброс. Мы, однако, считаем это излишним, поскольку в этом случае будет считаться «вышедшим из под контроля» процесс, имеющий низкий разброс. По нашему мнению, при улучшении процесса, когда статистические разбросы уменьшаются, статистические контрольные границы целесообразно сужать, но делать это нужно не на основе отдельных точек, выпавших за нижнюю границу по разбросу, а на основе статистического анализа данных по процессу за достаточно длительный промежуток времени.

Верхняя контрольная граница (UCL):

если стандартная сигма не задана:

если стандартная сигма задана:

Здесь:

- карты

Представим вначале основные формулы, а затем дадим их объяснение.

- карта (средних значений)

Центральная линия:

- если стандартные значения не заданы

номинал, если он задан

UCL и LCL , если стандартная сигма не задана

, если стандартная сигма задана

- карта (размахов)

Центральная линия (CL):

если стандартная сигма не задана:

если стандартная сигма задана:

Нижняя контрольная граница (LCL) =0

Верхняя контрольная граница (UCL):

если стандартная сигма не задана:

если стандартная сигма задана:

Дадим теперь пояснения, к представленным выше формулам.

Функция распределения размаха есть.

Здесь и - функция и плотность распределения, - объем подгруппы (выборки).

Пусть – размах в стандартной нормальной выборке из элементов (стандартное нормальное распределение имеет нулевое среднее и единичную дисперсию). меняется от выборки к выборке, т.е. является случайной величиной. Математическое ожидание случайной величины обозначим как , а дисперсию величины как (в соответствии с известным сборником таблиц Большева и Смирнова ([35], стр. 226)):

Введенный выше коэффициент - это то же самое, что и коэффициент .

Остальные коэффициенты рассчитываются по формулам:

или ,

где

Смысл коэффициента заключается в том, что он позволяет приближенно выразить сигму через средний размах:

Преимущество этой оценки в ее простоте. Однако, для объема выборки более двух, ее эффективность уступает эффективности наилучшей оценке, основанной на среднеквадратичном отклонении (для примера e2=1; e5=0,96; e10=0,86; e15=0,77, т.е. при эффективности оценок совпадают, а уже при эффективность основанной на размахе оценки составляет только 77% от эффективности наилучшей оценки).