
- •Линейные пространства
- •1. Линейные пространства. Определение
- •4. Для всякого вектора
- •1.1. Задачи
- •2. Линейная зависимость. Базис и координаты вектора.
- •Примеры
- •Примеры
- •2.1. Задачи
- •3. Подпространства линейного пространства
- •Примеры
- •3.1. 3Адачи
- •4. Точечно-векторное аффинное пространство
- •4.1. Система координат в пространстве
- •4.2. Прямая и плоскость в Vn
- •4.3. Задачи
- •5. Евклидовы и унитарные пространства
- •5.1. Ортонормированный базис евклидова и унитарного пространств
- •5.2. Ортогональное дополнение
- •5.3. Проектирование вектора на подпространства
- •5.4. Задачи
- •Литература
- •Содержание
5.2. Ортогональное дополнение
Определение. Два множества F и G векторов евклидова пространства E называются ортогональными, если каждый вектор из F ортогонален каждому вектору из G.
Определение. Пусть F
– подпространство E.
Совокупность всех векторов подпространства
E, ортогональных
подпространству F,
называется ортогональным дополнением
![]() подпространства F.
подпространства F.
Всякое ортогональное дополнение является, в свою очередь, линейным подпространством.
Всякое произвольное евклидово пространство E разлагается в прямую сумму своего произвольного подпространства F и его ортогонального дополнения
![]()
Примеры
1. Требуется найти базис ортогонального
дополнения
![]() подпространства L,
натянутого на векторы
подпространства L,
натянутого на векторы
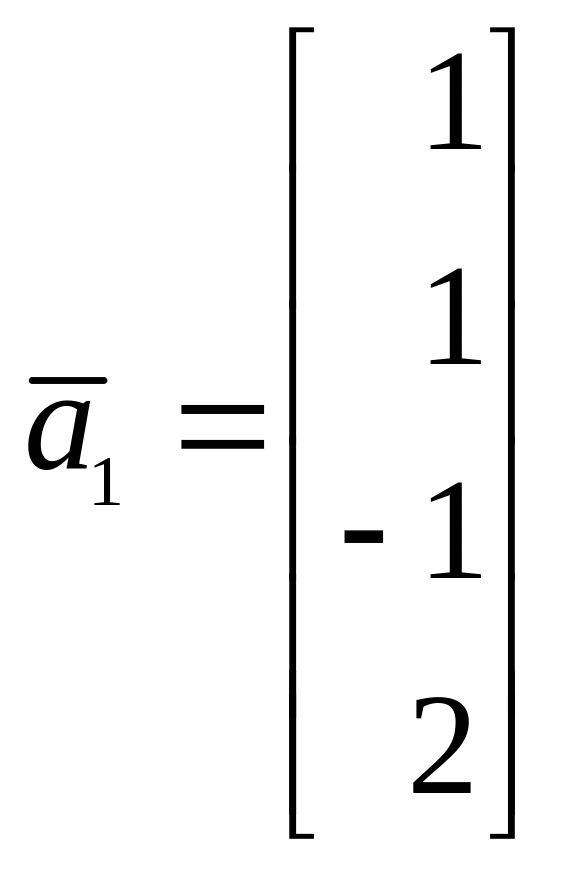 ,
,
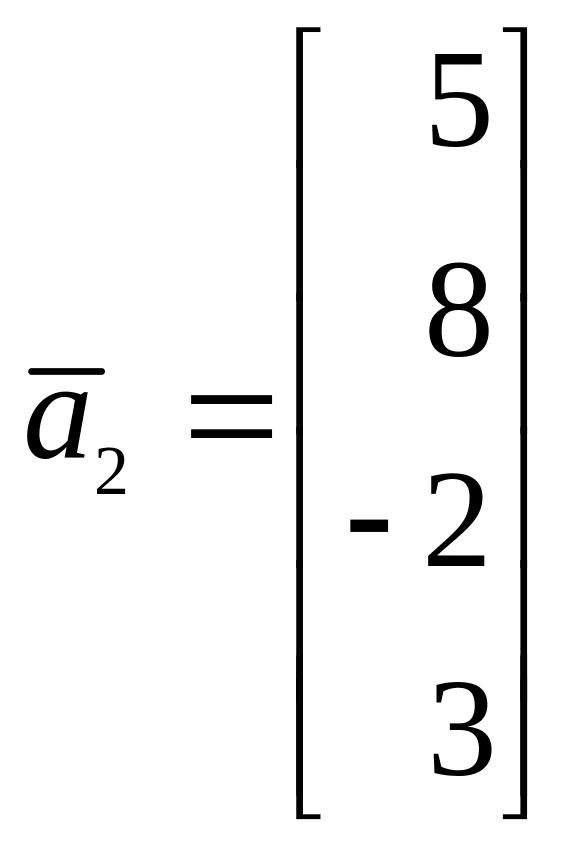 ,
,
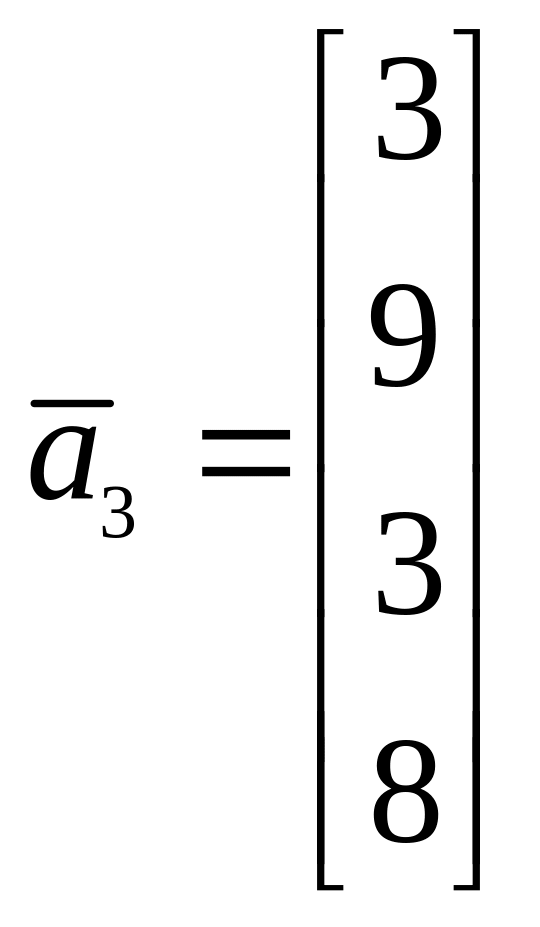
Будем считать, что базис, относительно
которого заданы векторы, ортонормированный.
По определению, если
![]() ,
то
,
то
![]() .
Далее, каждый вектор
из
должен быть ортогонален к
.
Для этого достаточно, чтобы
.
Далее, каждый вектор
из
должен быть ортогонален к
.
Для этого достаточно, чтобы
![]()
![]() .
Расписывая скалярные произведения,
получим три уравнения относительно
координат
.
Расписывая скалярные произведения,
получим три уравнения относительно
координат
![]() вектора
вектора
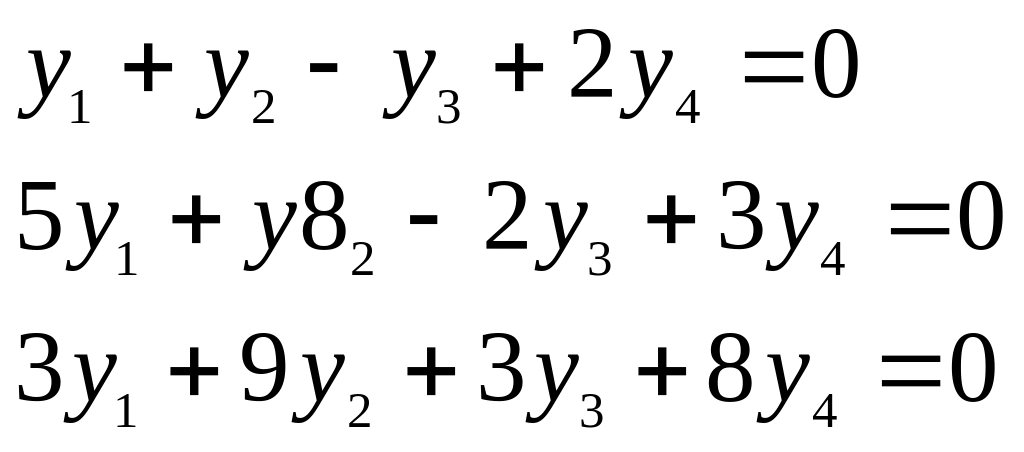
Совокупность решений этой системы и
образует ортогональное дополнение. За
базис в
можно принять любую фундаментальную
систему решений. Например, вектор
![]() .
.
2. Линейное подпространство
![]() задано уравнениями
задано уравнениями
![]()
Требуется найти уравнения, которые задают ортогональное дополнение .
Пусть
![]() ,
,
![]() .
Тогда
.
Этому условию удовлетворяют два линейно
независимых вектора
.
Тогда
.
Этому условию удовлетворяют два линейно
независимых вектора
![]() и
и
![]() ,
которые образуют коэффициенты системы
уравнений, задающей F.
Далее,
,
которые образуют коэффициенты системы
уравнений, задающей F.
Далее,
![]() .
Ранг системы равен 2. Значит
.
Ранг системы равен 2. Значит
![]() и, так как
и, так как
![]() ,
то
,
то
![]() .
Поэтому найденные векторы можно принять
за базис в
,
и
есть линейная оболочка данных векторов.
Далее задача решается так же как в
примере из § 3. Дословно повторяя решение,
получим следующую систему уравнений
.
Поэтому найденные векторы можно принять
за базис в
,
и
есть линейная оболочка данных векторов.
Далее задача решается так же как в
примере из § 3. Дословно повторяя решение,
получим следующую систему уравнений
![]()
которая и задает .
5.3. Проектирование вектора на подпространства
Пусть
![]() .
Тогда всякий вектор
.
Тогда всякий вектор
![]() можно представить в виде
можно представить в виде
![]() ,
где
,
где
![]() и
и
![]() .
Вектор
.
Вектор
![]() называется ортогональной проекцией
вектора x на
подпространство L, а
вектор
называется ортогональной проекцией
вектора x на
подпространство L, а
вектор
![]() называется ортогональной составляющей
вектора
.
называется ортогональной составляющей
вектора
.
Пусть
![]() и
и
![]() — расстояние между векторами
— расстояние между векторами
![]() ,
тогда
,
тогда
![]()
Таким образом, ортогональная проекция
есть ближайший к
вектору подпространства L.
Часто используются следующие обозначения
![]() ,
,
![]() .
.
Укажем в заключение как вычисляются
координаты вектора
![]() .
Пусть
.
Пусть
![]() — базис в L. Так как
— базис в L. Так как
![]() ,
то
,
то
![]() .
Поэтому
.
Поэтому
![]()
Отсюда имеем, что в случае ортонормированного базиса
![]()
Примеры
1. Найти ортогональную проекцию
и ортогональную составляющую
![]() вектора
на линейное подпространство L,
натянутое на векторы
вектора
на линейное подпространство L,
натянутое на векторы
![]() .
Все векторы заданы координатами
относительно ортонормированного базиса.
.
Все векторы заданы координатами
относительно ортонормированного базиса.
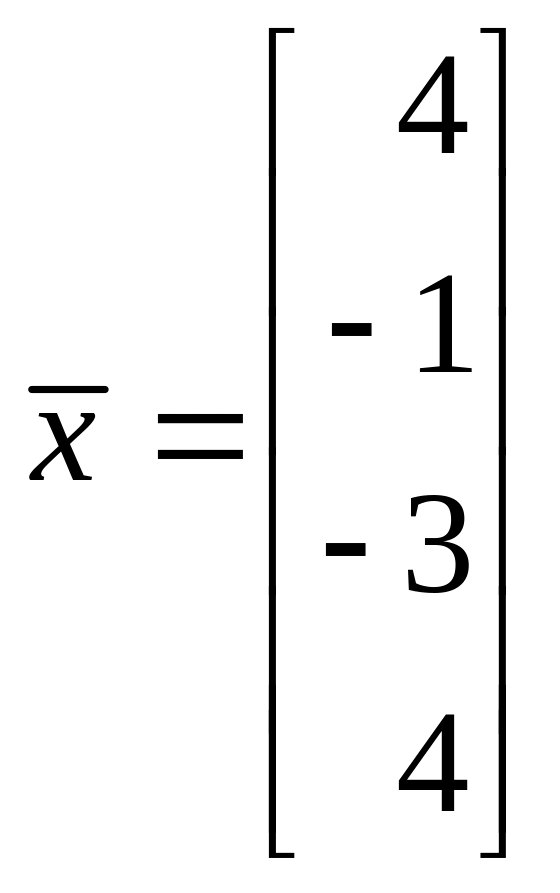 ,
,
,
,
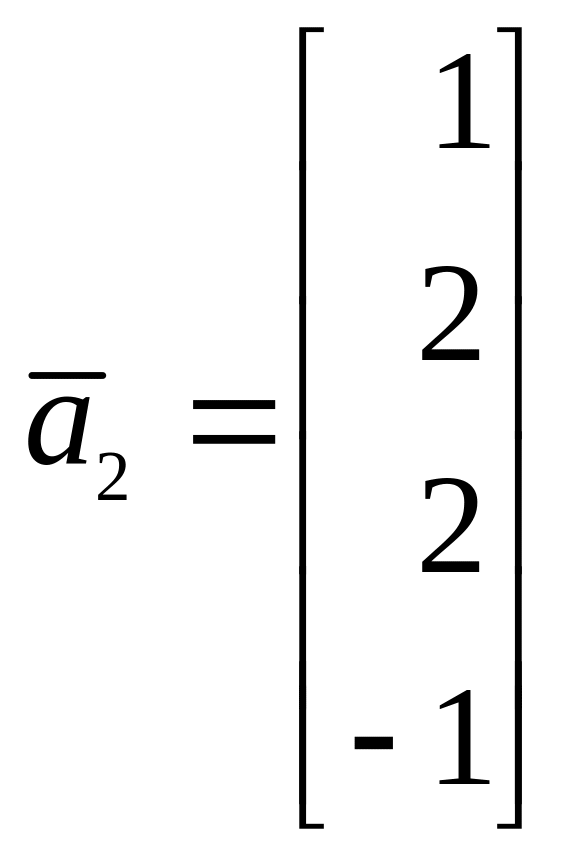 ,
,
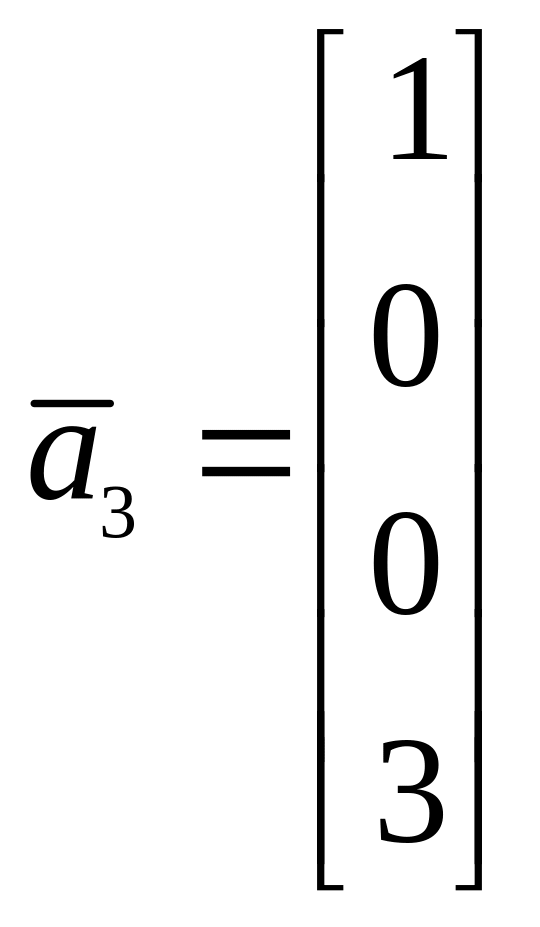
Нетрудно убедиться, что
![]() и что за базис можно принять векторы
и
.
Нам будет удобно перейти к ортонормированному
базису в L. Применяя
процедуру ортогонализации к векторам
и
,
получим ортонормированный базис в L:
и что за базис можно принять векторы
и
.
Нам будет удобно перейти к ортонормированному
базису в L. Применяя
процедуру ортогонализации к векторам
и
,
получим ортонормированный базис в L:
![]() ,
,
![]()
Заметьте, что векторы
и
![]() линейно выражаются через
и
и, значит, также принадлежат L.
Имеем теперь
линейно выражаются через
и
и, значит, также принадлежат L.
Имеем теперь
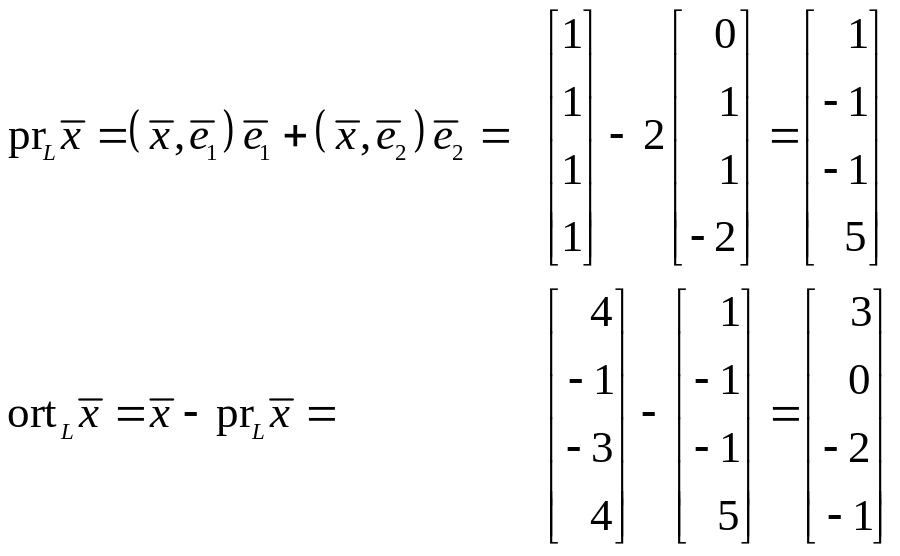
2. Требуется найти расстояние от точки,
заданной вектором
![]() до плоскости (линейного многообразия),
заданной системой уравнений
до плоскости (линейного многообразия),
заданной системой уравнений
![]()
Расстояние между точкой и множеством L определится следующим образом
![]()
Для вычисления расстояния удобно перейти
к параметрическому уравнению плоскости.
Имеем
и поэтому всякий вектор
![]() представляется в виде
представляется в виде
![]()
где
![]() — фиксированный радиус-вектор точки
плоскости;
и
— базис направляющего линейного
подпространства, которое задается
соответствующей однородной системой.
Решая уравнение, получим, например,
— фиксированный радиус-вектор точки
плоскости;
и
— базис направляющего линейного
подпространства, которое задается
соответствующей однородной системой.
Решая уравнение, получим, например,
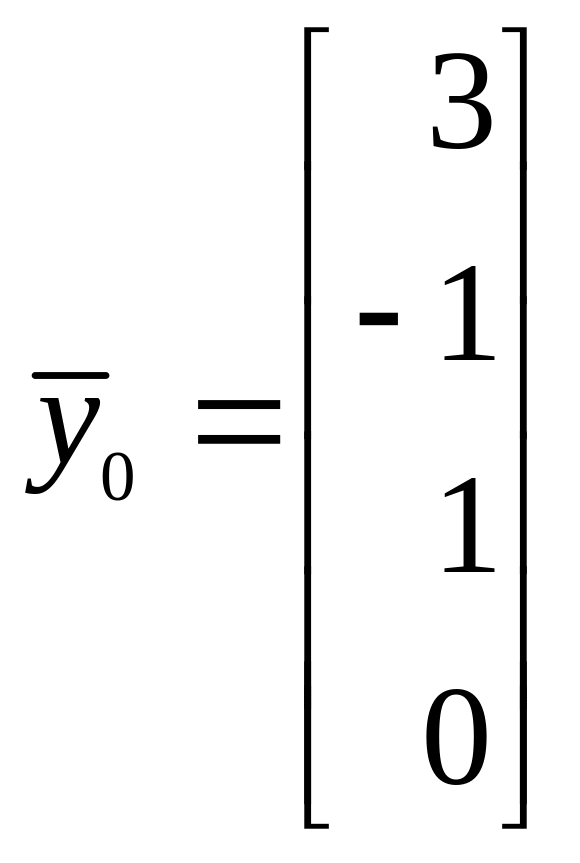 ,
,
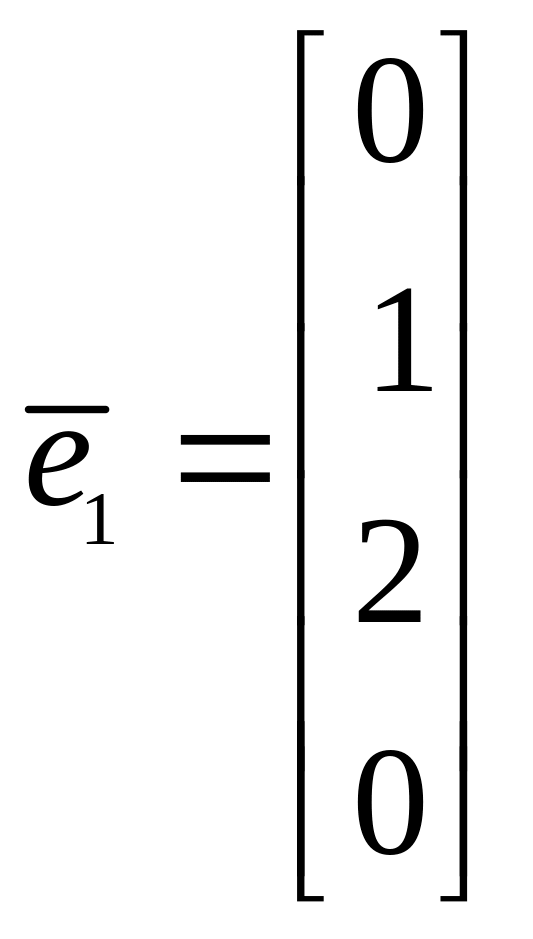 ,
,

Затем
![]()
Векторы
и
принадлежат направляющему подпространству
M плоскости L.
Вектор
![]() .
Так как
.
Так как
![]() ,
а
,
а
![]() ,
то
,
то
![]()
Правая часть этого неравенства и есть
искомое расстояние. Осталось вычислить
вектор
![]() и найти его норму. Проделав для этого
аналогичные вычисления и вычислив длину
вектора, получим, что
и найти его норму. Проделав для этого
аналогичные вычисления и вычислив длину
вектора, получим, что
![]() .
.
3. Пусть
![]() — ортонормированная система векторов
евклидова пространства En.
Нужно доказать, что для любого вектора
имеет место неравенство Бесселя
— ортонормированная система векторов
евклидова пространства En.
Нужно доказать, что для любого вектора
имеет место неравенство Бесселя
![]()
с равенством тогда и только тогда, когда
![]() ,
т.е. векторы
образуют ортонормированный базис в En.
,
т.е. векторы
образуют ортонормированный базис в En.
Так как
![]() — ортонормированная система, то ее
всегда можно векторами
— ортонормированная система, то ее
всегда можно векторами
![]() достроить до ортонормированного базиса
в En.
Разложим вектор
по этому базису. Имеем
достроить до ортонормированного базиса
в En.
Разложим вектор
по этому базису. Имеем
![]()
Далее,
![]()
или
![]()
С равенством тогда и только тогда, когда
.
Исключение составляют случаи, когда
![]()
![]() или когда
принадлежит линейной оболочке векторов
или когда
принадлежит линейной оболочке векторов
![]() .
.
