4.3. Задачи
Найти точку пересечения двух прямых
и
.
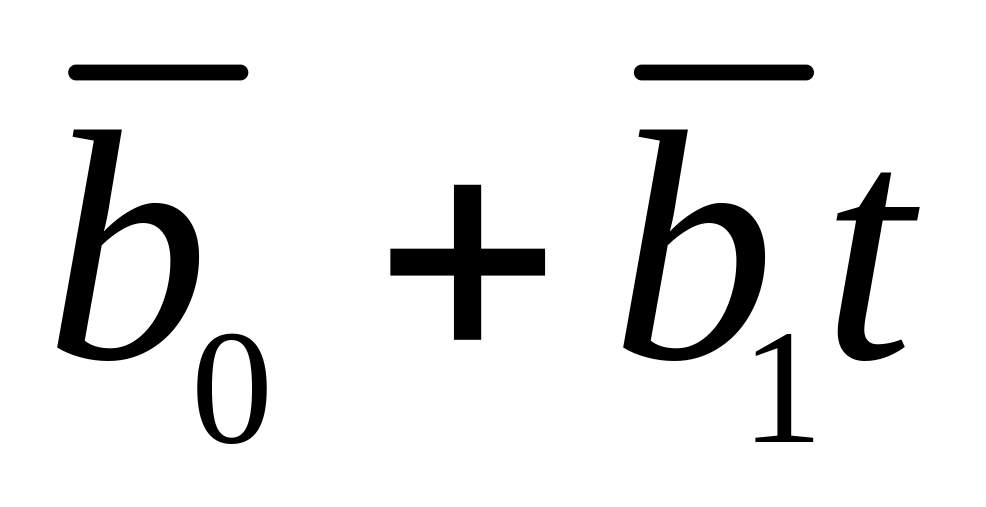а)
,
,
,
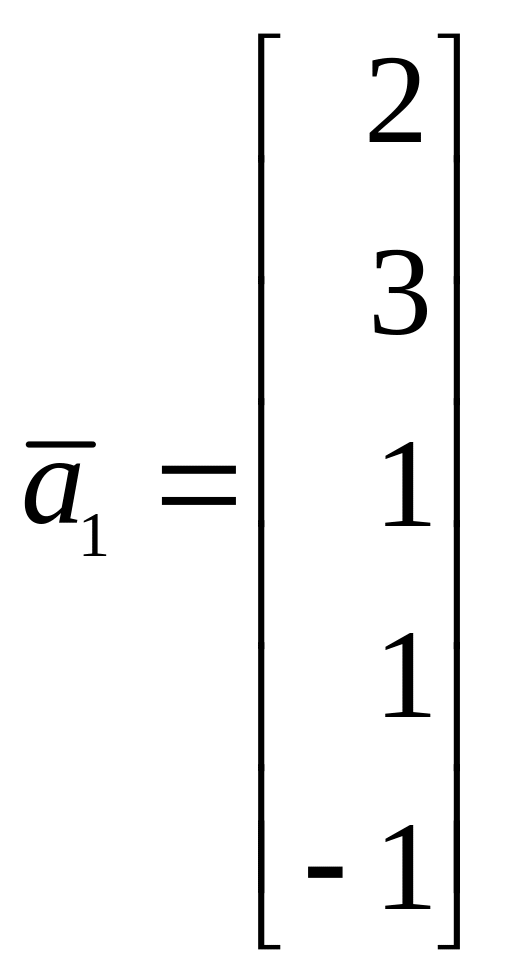б)
,
,
,
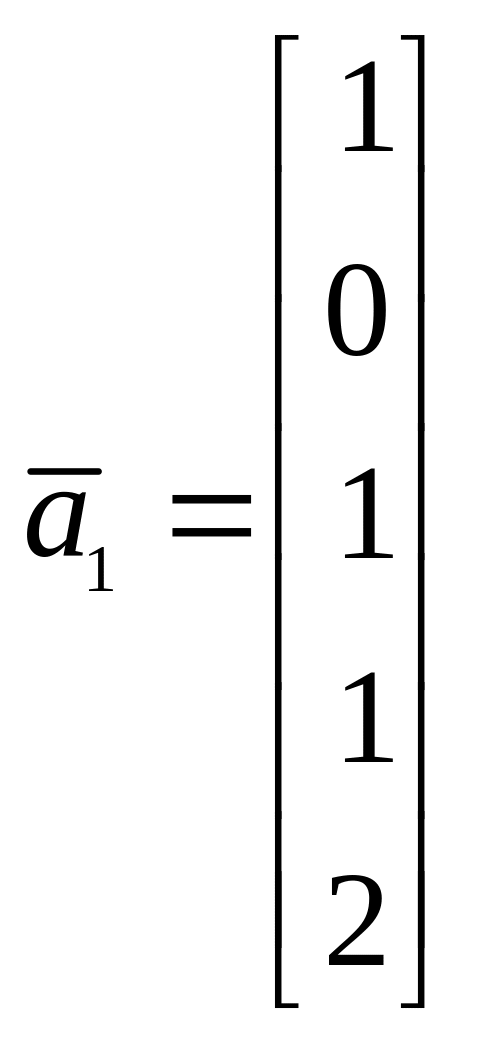2. Найти прямую, проходящую через точку,
заданную вектором
и пересекающую прямые
и
,
и найти точки пересечения искомой прямой
с двумя данными
а) 
,
,
,
,
б) 
,
,
,
,
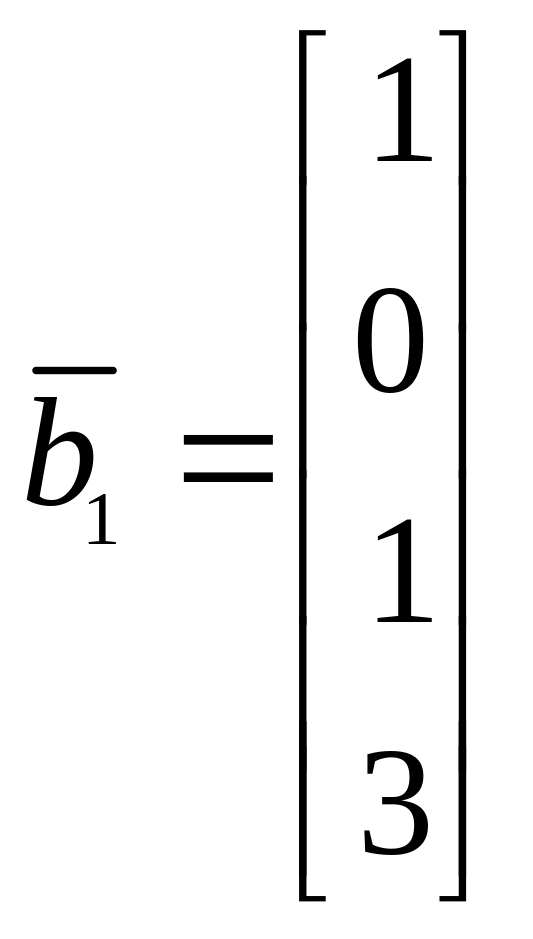3. Описать все случаи взаимного расположения двух плоскостей
,
в n-мерном пространстве и указать необходимые и достаточные условия для каждого из этих случаев.
4. Доказать, что всякая система
точки пространства Vn
определяет плоскость размерности
.
5. Доказать, что линейное многообразие
может быть охарактеризовано как множество
векторов, содержащее вместе с любыми
двумя векторами
и
их линейные комбинации
при любых α.
6. Найти параметрические уравнения плоскости, заданной общими уравнениями:
7. Найти общие уравнения плоскости, заданной параметрическими уравнениями в координатной форме
5. Евклидовы и унитарные пространства
Определение. Вещественная функция
двух векторных аргументов
и
,
заданная на линейном пространстве E,
называется скалярным произведением,
если выполняются следующие условия:
1.
2.
,
–
вещ. число
3.
4.
,
Определение. Вещественное линейное пространство E, на котором задано скалярное произведение, называется евклидовым пространством.
Пример. Рассмотрим арифметическое пространство Rn и определим скалярное произведение векторов и соотношением
Прямой подстановкой убеждаемся, что условия 1-4 выполняются. Получим n-мерное евклидово пространство, которое обычно обозначается как En.
В случае комплексного линейного пространства скалярное произведение определяется несколько иным образом.
Определение. Комплексная функция двух векторных аргументов и , заданная на комплексном линейном пространстве U, называется скалярным произведением, если выполняются следующие условия:
1.
2.
,
— комплексное
число
3.
4. ,
Комплексное линейное пространство U, на котором задано скалярное произведение, называется унитарным пространством.
Во всяком унитарном (евклидовом) пространстве имеет место неравенство Коши-Шварца:
с равенством лишь в случае, когда
.
Введение скалярного произведения позволяет распространить на линейные пространства различные метрические понятия:
1. Норма (длина) вектора определяется как
Введенная функция удовлетворяет следующим условиям
1.
,
2.
3.
2. Угол φ между векторами и евклидова пространства определяется как угол, изменяющийся в пределах от нуля до π, косинус которого
3. Расстояние между точками аффинного пространства и , связанного с данным евклидовым, определяется как
5.1. Ортонормированный базис евклидова и унитарного пространств
Определение. Вектор
называется нормированным, если 
.
Определение. Два вектора
и
называются ортогональными, если
.
Определение. Система векторов евклидова (унитарного) пространства называется ортогональной, если она либо состоит из одного ненулевого вектора, либо ее векторы попарно ортогональны. Ортогональная система, состоящая из нормированных векторов, называется ортонормированной. Для нее
Всякая ортогональная система линейно независима.
Определение. Базис евклидова (унитарного) пространства, векторы которого образуют ортонормированную систему, называется ортонормированным базисом.
Заметьте себе, что, в зависимости от того, как введено скалярное произведение, различные системы векторов могут быть или не быть ортонормированными.
Процедура ортогонализации Грама-Шмидта.
Для построения ортонормированной
системы векторов и, в частности,
ортонормированного базиса
может быть использована следующая
процедура. Пусть векторы
— линейно независимы. Первый вектор
ортонормированной системы
Второй вектор
,
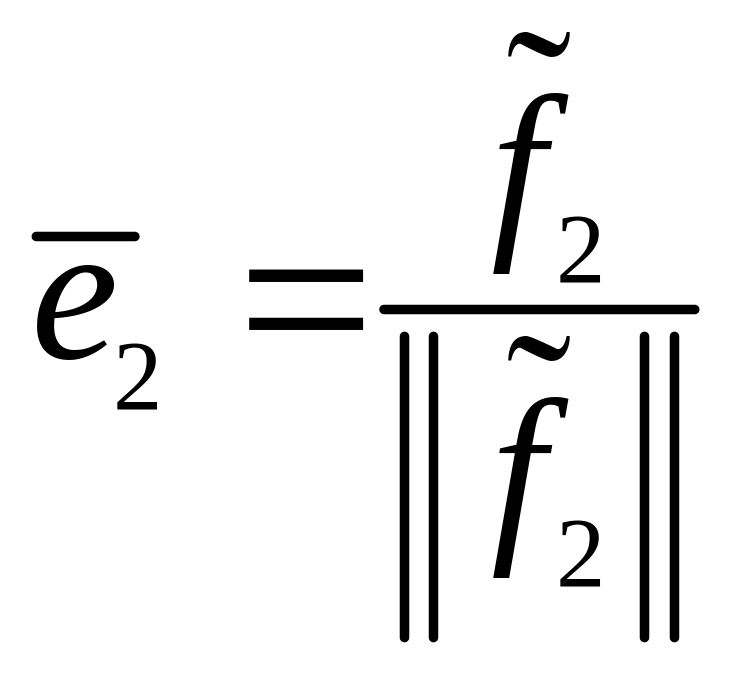Наконец, векторы
определяются соотношениями
,
Пример. Необходимо ортогонализировать систему векторов
,
,
Скалярное произведение векторов
и
определяется как
Для построения первого вектора
считаем
.
Вектор
Для построения второго вектора вычислим
вначале
.
Вектор
и вектор
Для построения третьего вектора вычислим
и
.
Вектор
И вектор
Во всяком ортонормированном базисе
унитарного (евклидова) пространства
скалярное произведение векторов
и
с координатами
и
Координаты вектора
