2. Линейная зависимость. Базис и координаты вектора.

Рассмотрим линейное пространство X над полем K. Пусть , . Линейной комбинацией векторов пространства X называется сумма вида

Числа называются коэффициентами линейной комбинации.

Определение. Элементы пространства X называются линейно зависимыми, если существуют числа не все равные нулю одновременно такие, что линейная комбинация

(2.1)

Если же равенство (2.1) выполнено только тогда, когда все числа , то векторы называются линейно независимыми.

Необходимым и достаточным условием линейной зависимости векторов является равенство одного из них линейной комбинации других.

Примеры

1. Рассмотрим пространство геометрических векторов V₃. В нем два вектора линейно зависимы, когда они коллинеарны; три вектора линейно зависимы, когда они компланарны. Всякие четыре вектора этого пространства всегда линейно зависимы.

2. Рассмотрим арифметическое пространство R_n. Попытаемся построить линейно независимую систему векторов этого пространства. Рассмотрим k векторов

,

Если линейно зависимы, то одновременно такие, что

где – ноль пространства R_n. По определению R_n отсюда следует, что

,

Получаем в результате относительно t_i систему n линейных однородных уравнений с k неизвестными и матрицей размера . Такая система имеет только нулевое решение, если

и имеет ненулевое решение, если

Отсюда следует, что в пространстве R_n не может быть больше, чем n линейно независимых векторов. Линейно независимыми являются всякие векторы, компоненты которых образуют матрицу полного ранга. Например, n векторов

(2.2)

Определение. Совокупность линейно независимых векторов пространства X называется базисом этого пространства, если найдутся такие числа , что справедливо равенство

(2.3)

Соотношение (2.3) называется разложением вектора по базису.

В силу линейной независимости векторов базиса разложение (2.3) определяется единственным образом.

Определение. Коэффициенты разложения вектора по базису называются координа­тами вектора относительно базиса.

Пример. Совокупность векторов (2.2) образует очевидно базис пространства R_n, так как для всякого вектора имеет место разложение

При решении задач полезно помнить, что векторы линейно зави­симы тогда и только тогда, когда линейно зависимы вектор-столбцы из их координат относительно произвольного базиса.

Определение. Если в линейном пространстве X существует n линейно независимых векторов, а всякие век­тор этого пространства линейно зависимы, то число, n называется размерностью линейного пространства

Само линейное пространство X называется при этом n-мерным. Линейное пространство, в котором можно указать сколь угодно большое число линейно независимых векторов называется бесконечно мерным.

Примеры

1. Пространство V₃. В этом пространстве вся­кие три некомпланарных вектора линейно независимы, а всякие че­тыре вектора линейно зависимы. Следовательно, .

2. Пространство R_n. В этом пространстве всякие вектор линейно зависимы и существуют системы из n линейно независимых векторов, например, система векторов (2). Следовательно,

Если в линейном пространстве X существует базис из n векторов, то , обратно, если , то вся­кая система из n линейно независимых векторов образует базис пространства X.

Всякие два базиса и пространства X связаны между собой симметричными формулами

(2.4)

(2.5)

где невырожденные матрицы и являются взаимно обратными, i-й столбец матрицы A образуют координаты вектора в базисе из векторов . Формулы (2.4) и (2.5) называются формулами перехода, матрицы A и — матрицами перехода.

Если и – координаты вектора в базисах и , соответственно, то

(2.6)

(2.7)

Пример: Доказать, что каждая из данных двух систем векторов является базисом R₃ и найти связь координат одного и того же вектора в этих двух базисах:

Для доказательства того, что данные системы векторов являются базисными, вычислим, как и в предыдущем примере, ранги матриц

и

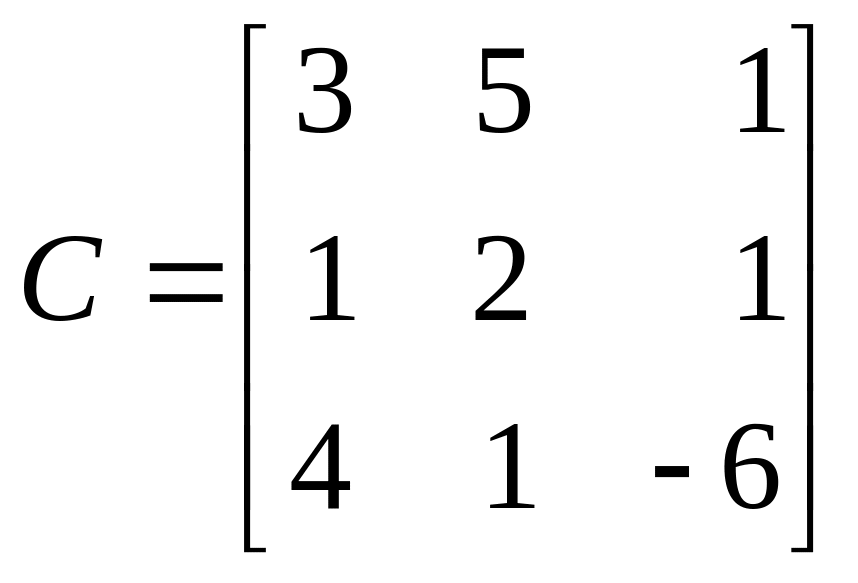
Нетрудно убедиться, что , и, следовательно, в R₃ данные системы векторов образуют базисы. Для определения связи координат необходимо получить формулы перехода (2.4) и (2.5). Имеем

Откуда получаем систему девяти скалярных уравнений

Решая системы уравнений, получаем матрицу перехода

и связь между «старыми» и «новыми» координатами: