
- •Линейные пространства
- •1. Линейные пространства. Определение
- •4. Для всякого вектора
- •1.1. Задачи
- •2. Линейная зависимость. Базис и координаты вектора.
- •Примеры
- •Примеры
- •2.1. Задачи
- •3. Подпространства линейного пространства
- •Примеры
- •3.1. 3Адачи
- •4. Точечно-векторное аффинное пространство
- •4.1. Система координат в пространстве
- •4.2. Прямая и плоскость в Vn
- •4.3. Задачи
- •5. Евклидовы и унитарные пространства
- •5.1. Ортонормированный базис евклидова и унитарного пространств
- •5.2. Ортогональное дополнение
- •5.3. Проектирование вектора на подпространства
- •5.4. Задачи
- •Литература
- •Содержание
3.1. 3Адачи
Доказать, что следующие системы векторов из Rn образуют линейные подпространства и найти их размерность и базис:
1. Все n-мерные векторы, у которых первая и последняя координата равны между собой.
2. Все n-мерные векторы, у которых координаты с четными номерами равны нулю.
3. Все n-мерные векторы вида
![]() ,
где и —
любые числа.
,
где и —
любые числа.
4. Показать, что всякое линейное пространство есть линейная оболочка любого своего базиса.
5. Показать, что решение системы
линейных однородных уравнений с n
неизвестными ранга K
образуют подпространство Rn
размерности
![]() .
.
6. Доказать, что если размерность суммы двух линейных подпространств пространства Rn на единицу больше размерности их пересечения, то сумма совпадает с одним из этих подпространств, а пересечение с другим.
7. Доказать, что пространство Rn
есть прямая сумма двух линейных
подпространств: L1 — заданного
уравнением
и L2, заданного
системой уравнений
![]() .
.
8. Найти размерность и базис линейного подпространства, натянутого на следующую систему векторов, заданных своими координатами
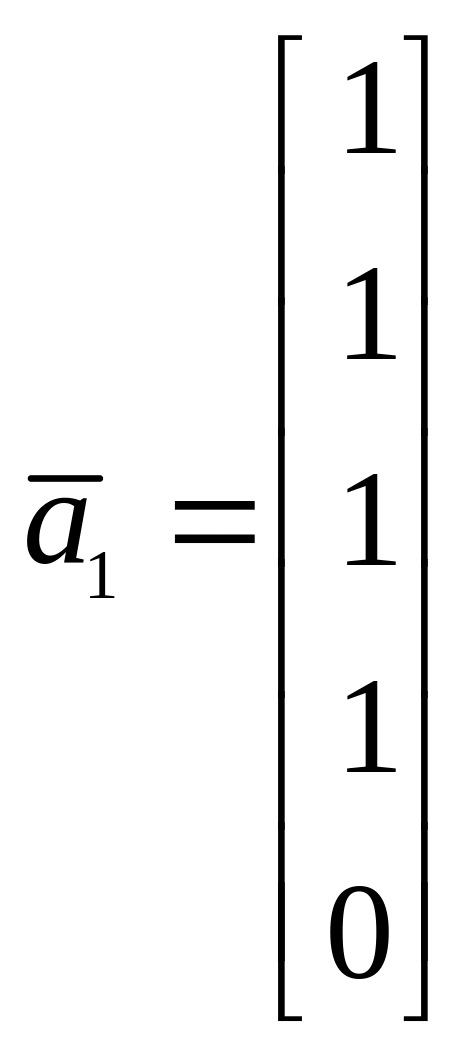 ,
,
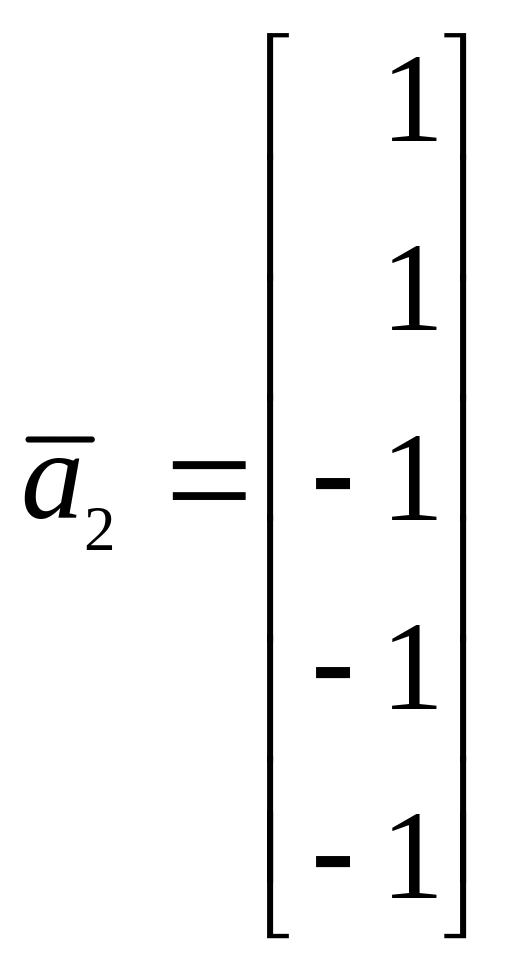 ,
,
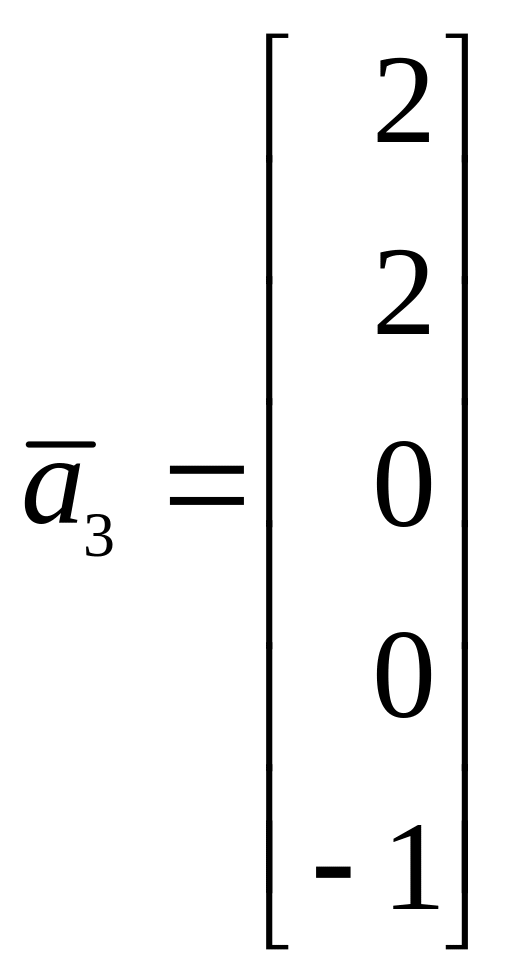 ,
,
 ,
,
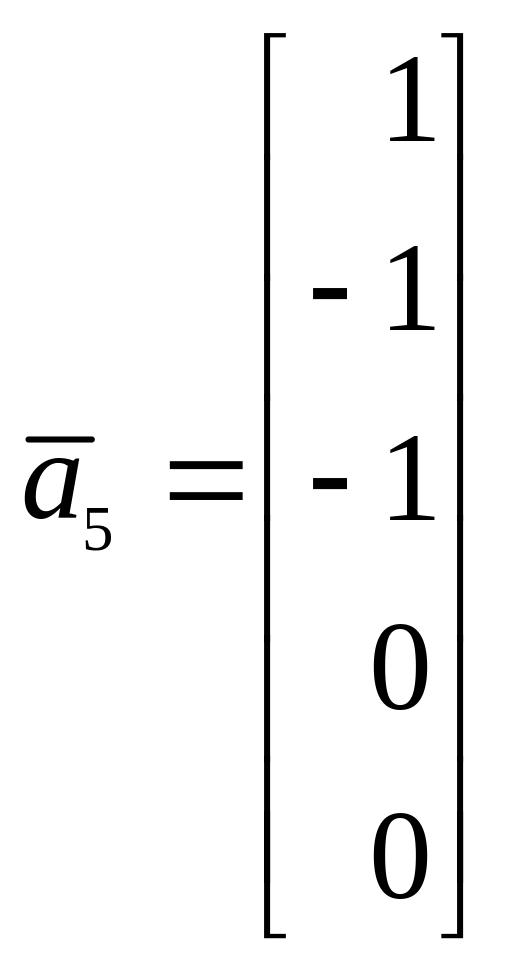
9. Найти систему линейных уравнений, задающую линейное подпространство, натянутое на следующую систему векторов:
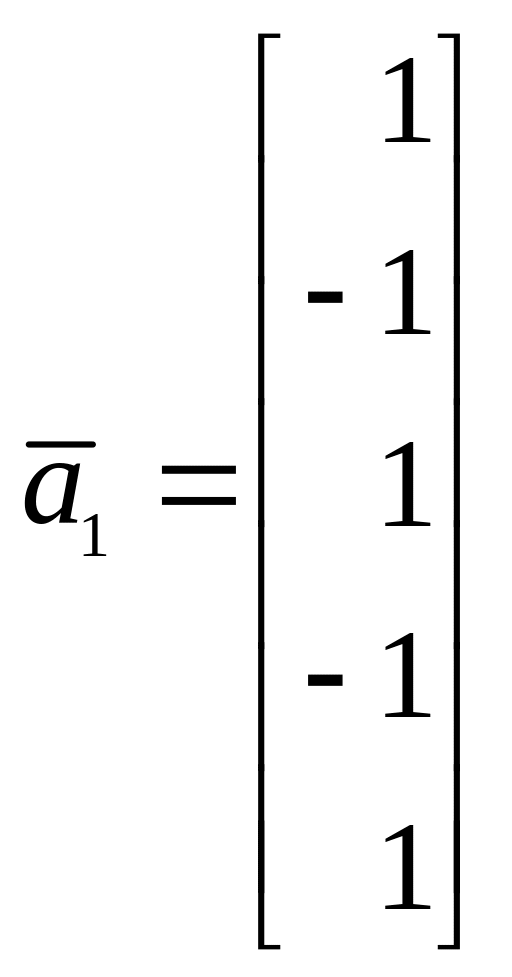 ,
,
 ,
,
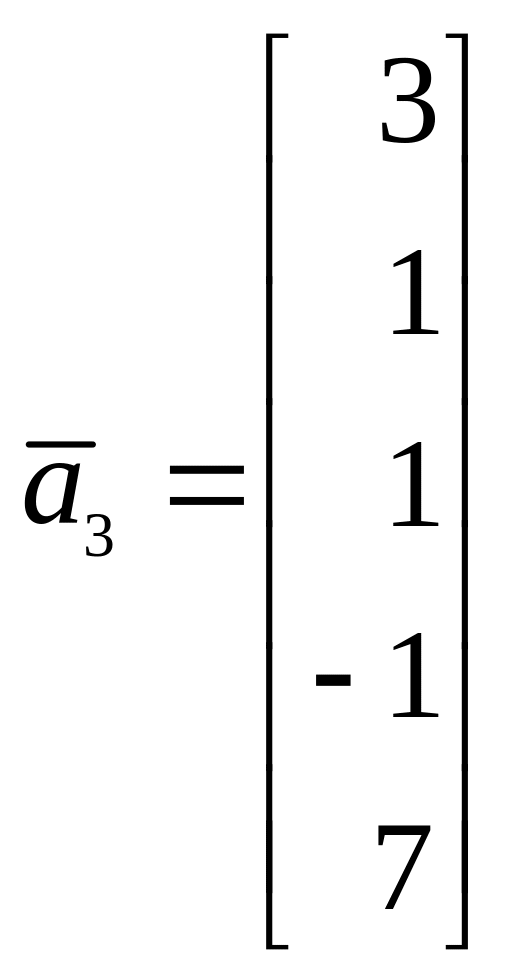 ,
,
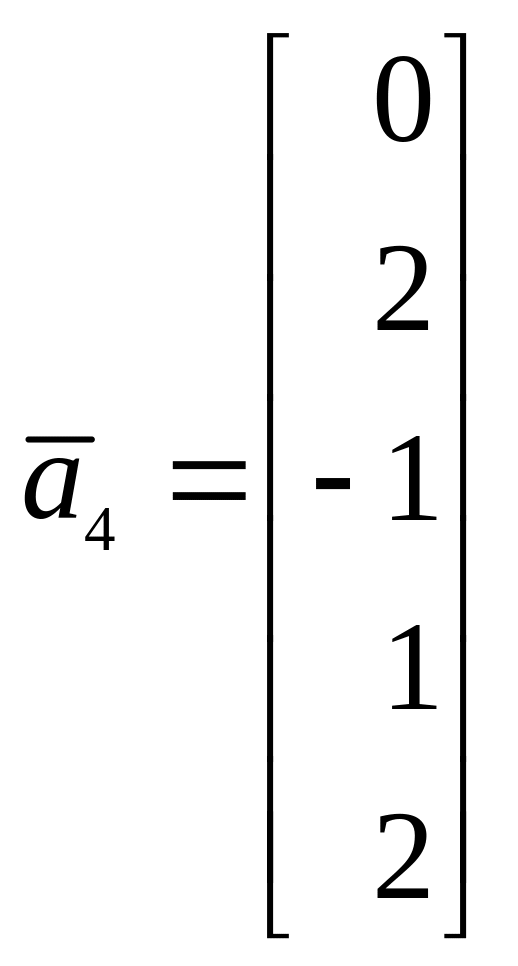
Найти размерности суммы и пересечения
линейных подпространств: L1,
натянутого на векторы
![]() и L2, натянутого
на векторы
и L2, натянутого
на векторы
![]()
10.
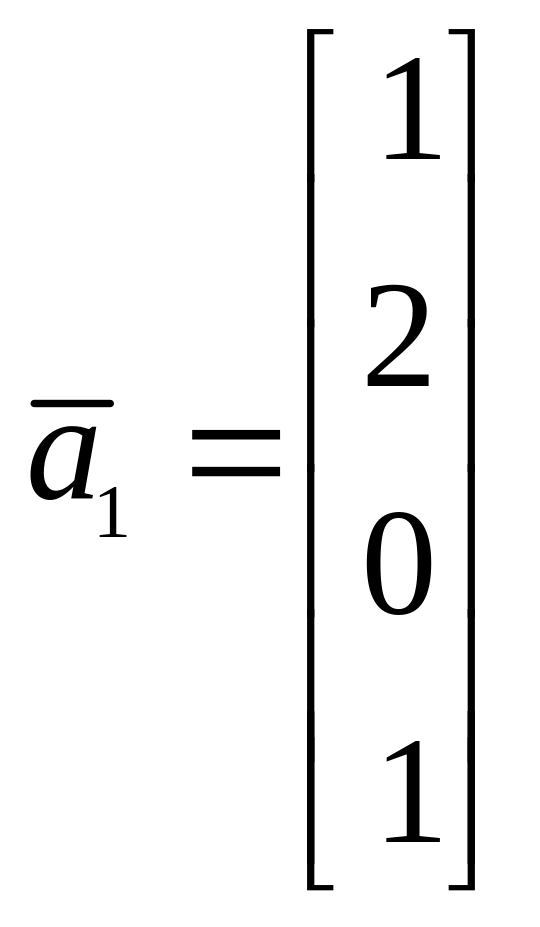 ,
,
 ,
,
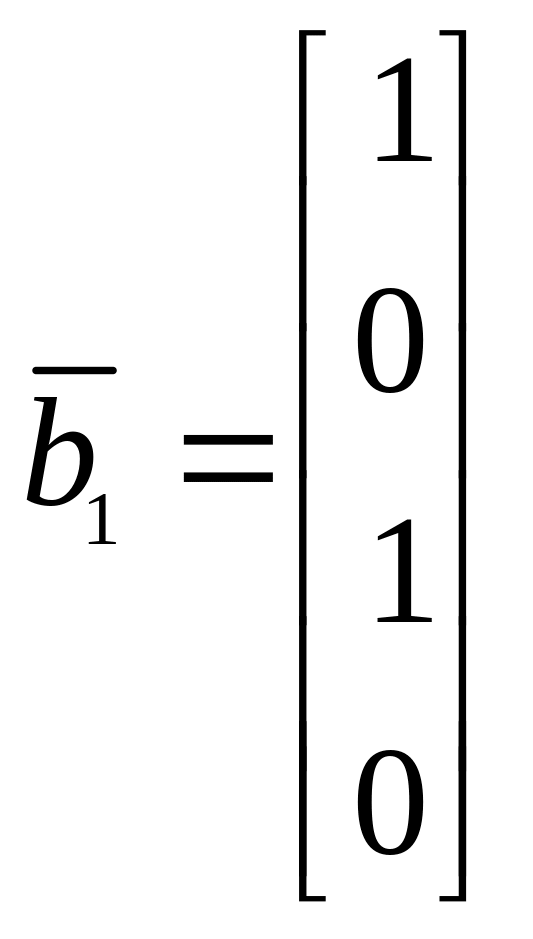 ,
,
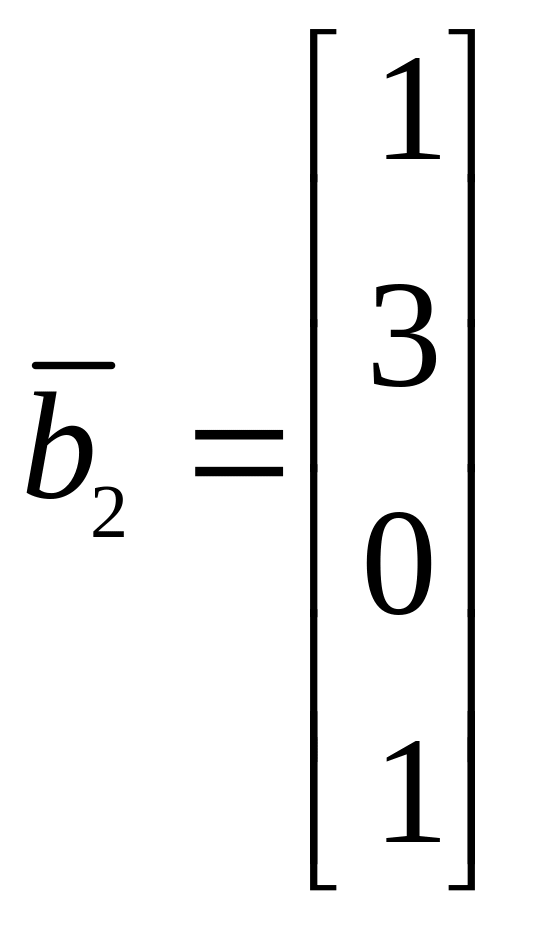
11.
![]() ,
,
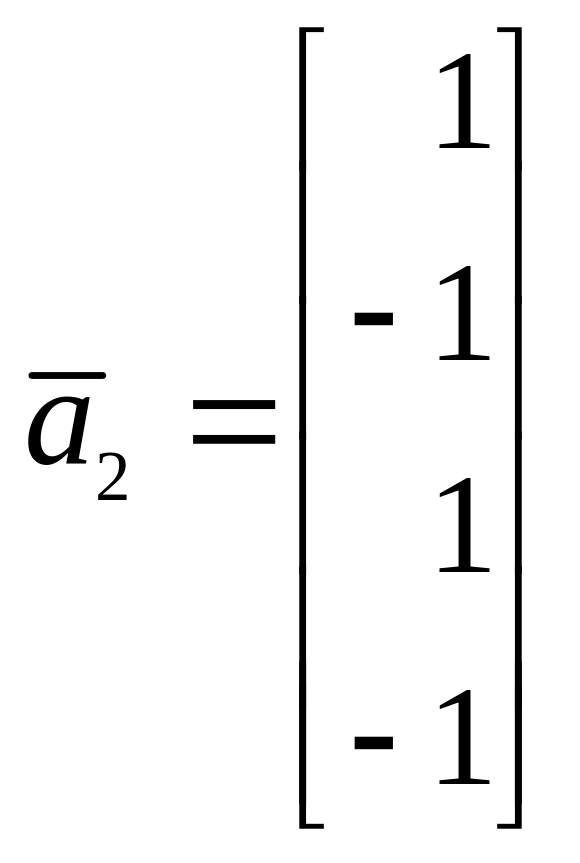 ,
,
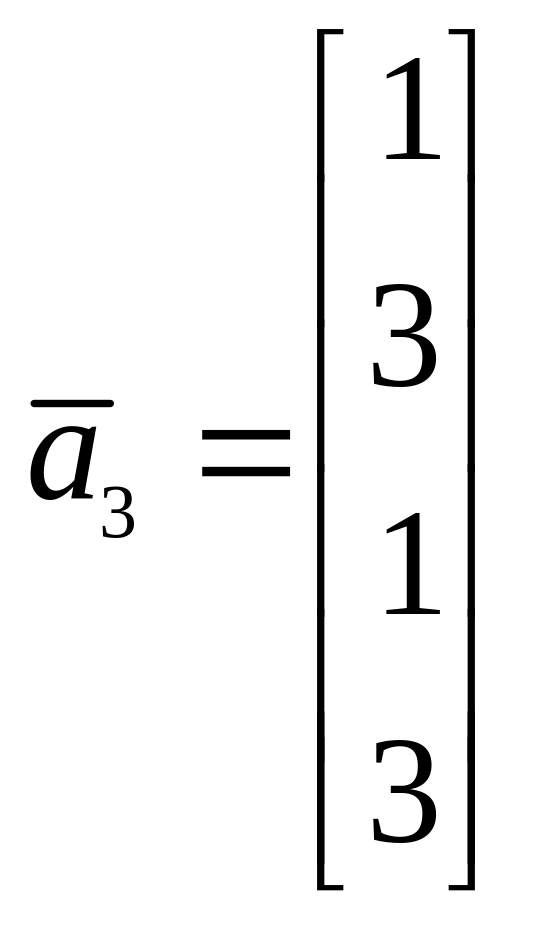 ,
,
 ,
,
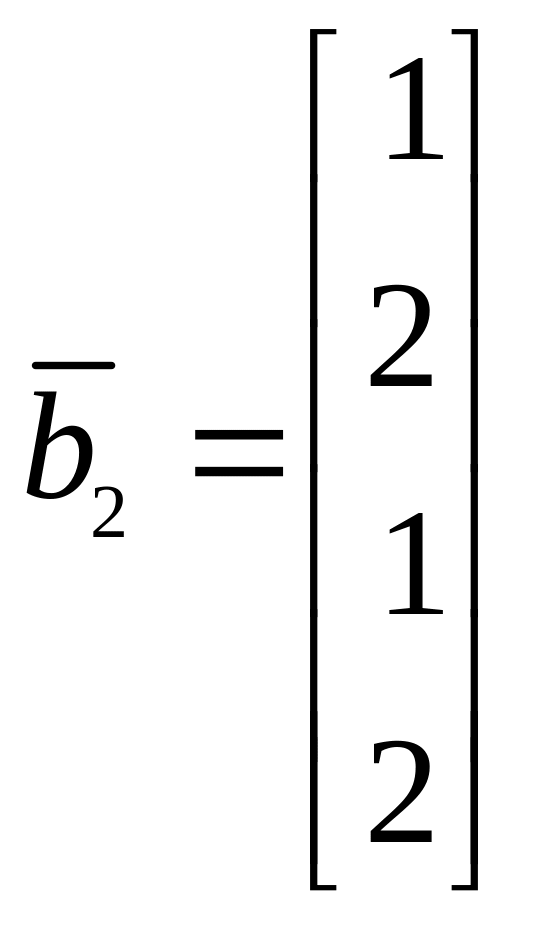 ,
,

Найти базисы суммы и пересечения линейных
подпространств, натянутых на системы
векторов
![]() и
и
![]()
12.
 ,
,
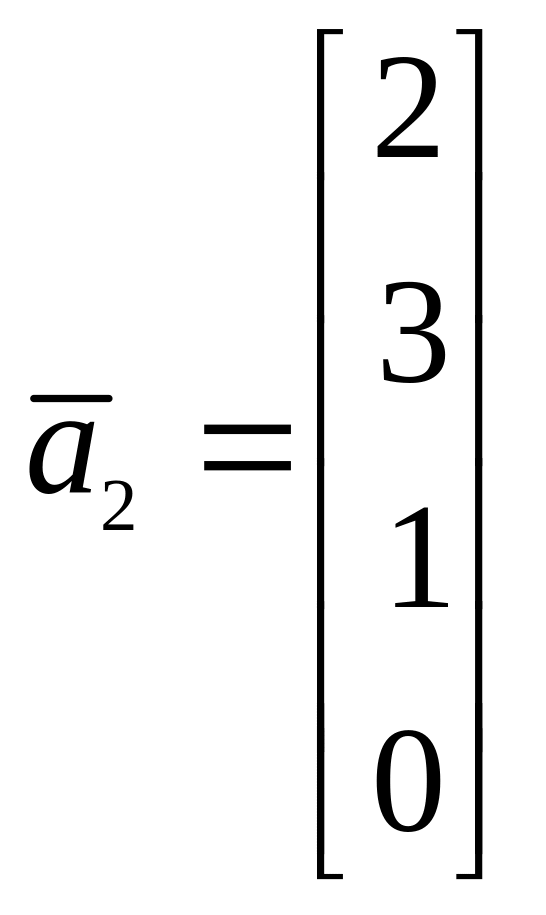 ,
,
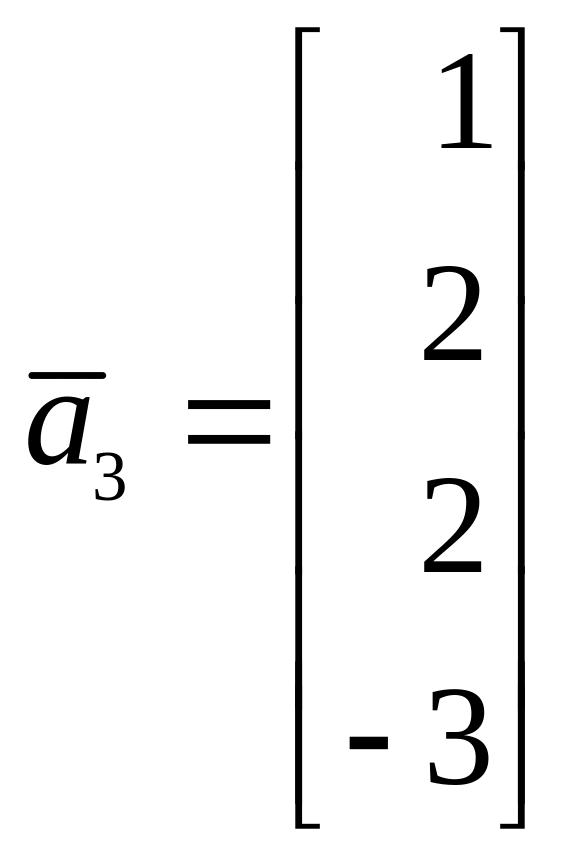 ,
,
![]() ,
,
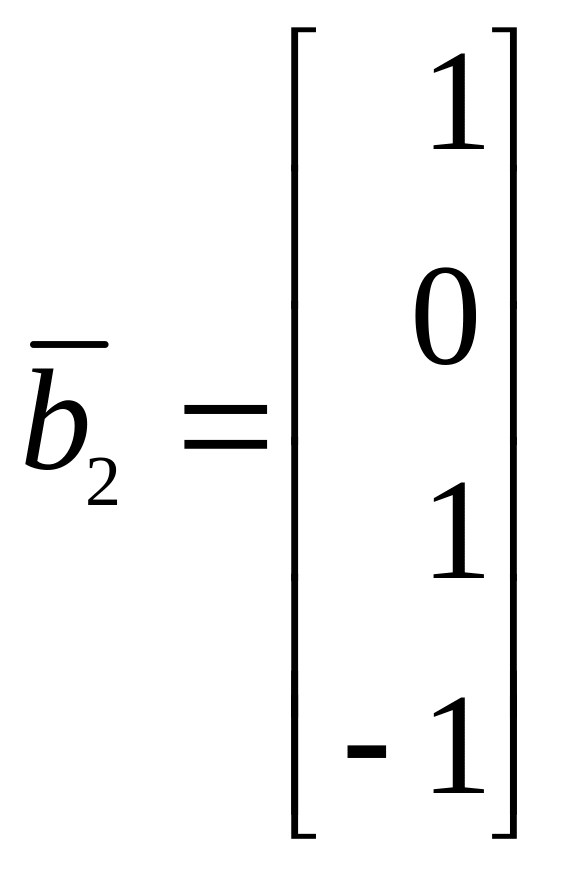 ,
,
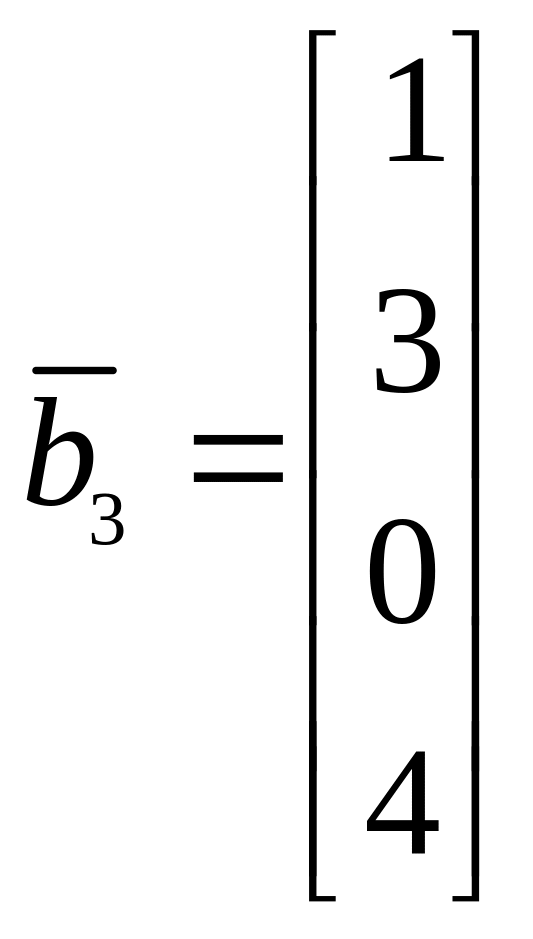
13.
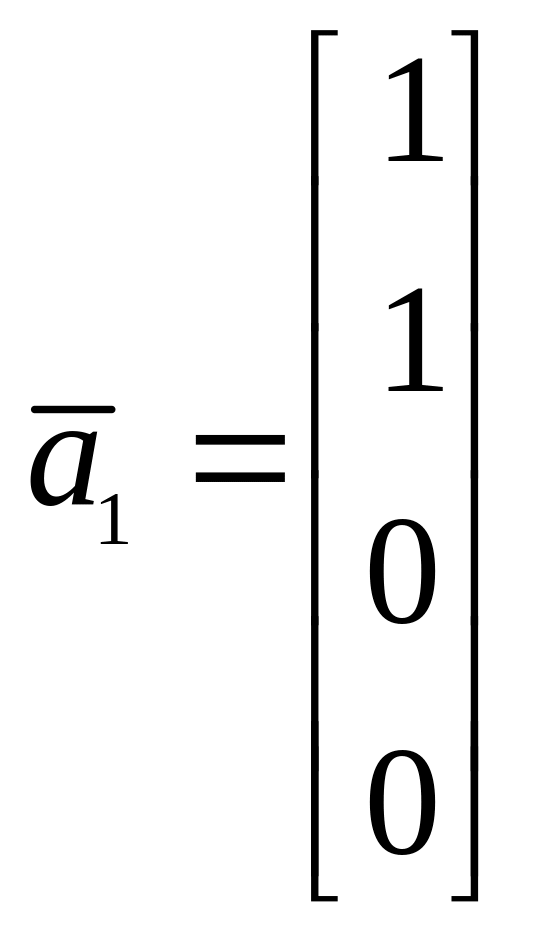 ,
,
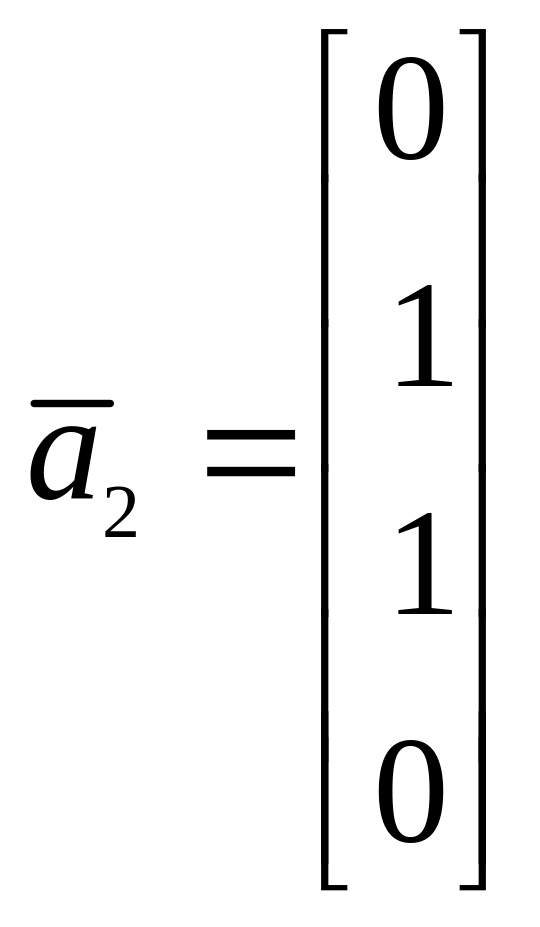 ,
,
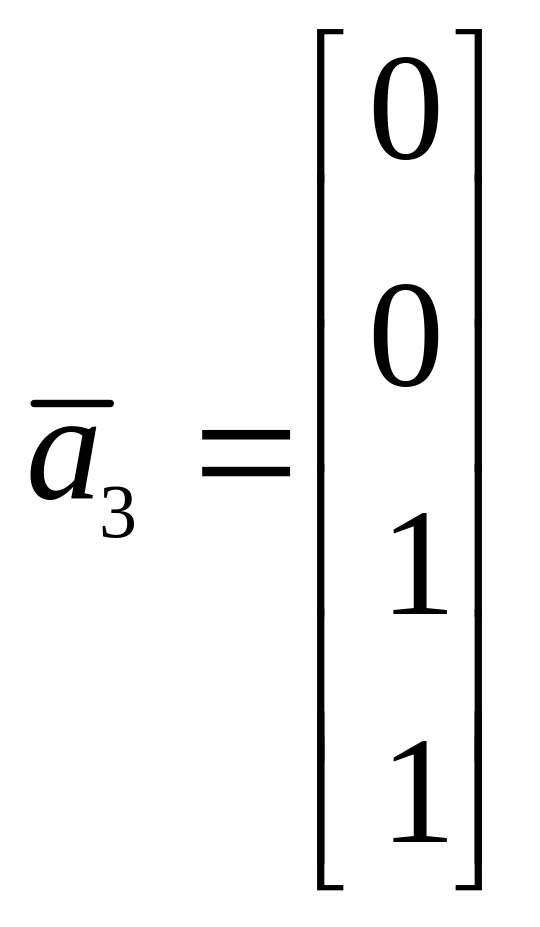 ,
,
,
,
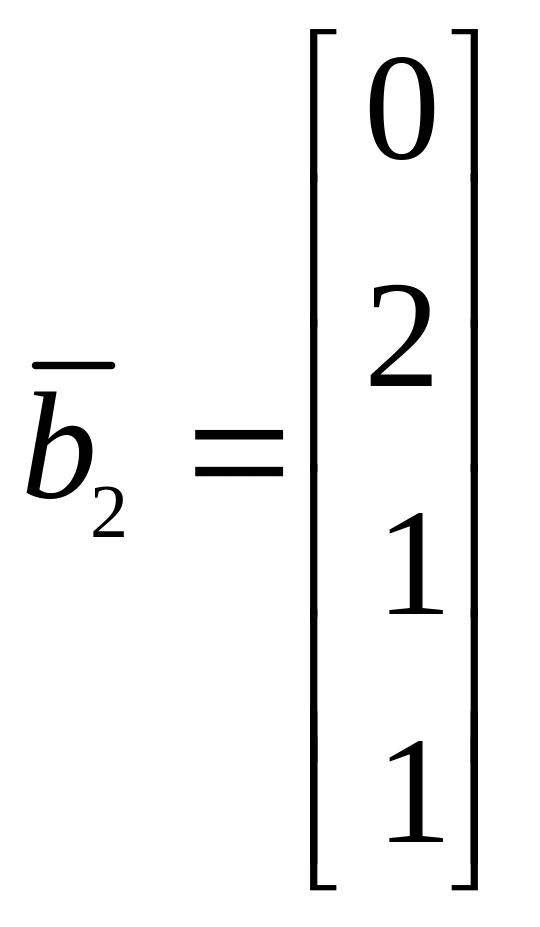 ,
,
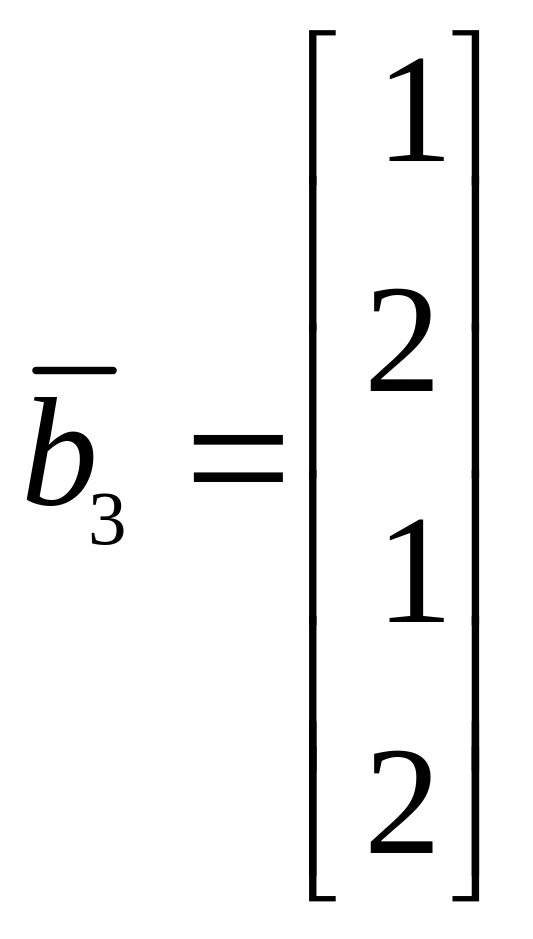
14. Линейным многообразием называется
совокупность векторов пространства
Rn, координаты которых
![]() удовлетворяют системе линейных уравнений
удовлетворяют системе линейных уравнений

Показать, что если к каждому вектору подпространства L пространства X прибавить фиксированный вектор, то получится линейное многообразие.
4. Точечно-векторное аффинное пространство
Определение. Пусть некоторое
множество
![]() состоит из элементов двух типов, которые
будем называть «точками» и «векторами».
Пусть при этом множество векторов
образует n-мерное линейное пространство,
а множество точек не пусто.
состоит из элементов двух типов, которые
будем называть «точками» и «векторами».
Пусть при этом множество векторов
образует n-мерное линейное пространство,
а множество точек не пусто.
Множество называется точечно-векторным аффинным пространством, если:
1. Каждая пара точек А1 и A2,
заданных в определенном порядке,
определяет единственный вектор
![]() .
.
2. Для
каждой точки А1, и каждого
вектора
существует единственная точка A2,
такая, что
![]() .
.
3. Если
![]() и
и
![]() ,
то
,
то
![]() .
.
Пространство называется n-мерным, если n-мерно соответствующее линейное пространство.
Пример. Данному определению удовлетворяет, очевидно, обычное геометрическое пространство, в котором векторы вводятся как упорядоченные пары точек. Вторая аксиома соответствует возможности отложить любой вектор из произвольной точки, а третья аксиома соответствует определению сложения векторов.
4.1. Система координат в пространстве
Если в пространстве Vn
зафиксировать некоторую точку O,
то в силу свойств 1 и 2 между всеми
остальными точками и векторами
устанавливается взаимно однозначное
соответствие. Вектор
![]() называется радиус-вектором точки А
относительно точки O.
называется радиус-вектором точки А
относительно точки O.
Определение. Системой координат в пространстве Vn, называется совокупность фиксированной точки O и некоторого базиса в Vn.
Координатами вектора в заданной системе координат пространства Vn называются координаты вектора относительно базиса .
Координатами точки А в данной системе ко- ординат пространства Vn называются координаты радиус-вектора точки относительно базиса.
Всякие два базиса пространства Vn
и
![]() связаны между собой формулами перехода
связаны между собой формулами перехода

где вектор-столбцы матриц перехода
и
![]() состоят из координат векторов
состоят из координат векторов
![]() и
соответственно в базисах
и
соответственно в базисах
![]() и
и
![]() .
.
Если даны две системы координат O,
и
![]() ,
,
то координаты любой точки
,
,
то координаты любой точки
![]() и
и
![]() относительно этих систем координат
связаны соотношениями
относительно этих систем координат
связаны соотношениями
![]() ,
,
где
![]() – координаты точки
в
– координаты точки
в
![]() – матрица перехода.
– матрица перехода.
