
- •Исследование операций
- •Учебный план
- •Тематические планы лекций Лекция № 1. Исследование операций как методологическая основа теории принятия управленческих решений. Основные термины, определения, формализация
- •Лекция № 2.Моделирование целевых установок развития сложных системах
- •Лекция № 3. Примеры моделей операций
- •Лекция № 4. Элементы выпуклого анализа
- •Лекция № 5. Основы выпуклого программирования. Теория Куна-Таккера
- •Лекция № 6. Линейное программирование
- •Лекция № 7. Игровые методы обоснования решений
- •Лекция № 8. Моделирование операций на основе марковских случайных процессов
- •Лекция № 9. Элементы теории массового обслуживания
- •Список источников и литературы
- •2. Дополнительная литература
- •Лекция № 1. Исследование операций как методологическая основа теории принятия управленческих решений. Основные термины, определения, формализация
- •1.1Цели и задачи курса «Исследование операций»
- •1.2Системный подход в решении проблем управления
- •1.2.1Формальное определение системы и примеры систем
- •1.2.2Основные понятия целевого подхода в управлении
- •1.2.3Концептуальная постановка проблемы
- •1.2.4Понятие структуризации проблемы
- •1.2.5Основные понятия объектно-субъектного подхода в управлении
- •1.2.6Формализация системы и фаз процесса принятия решений
- •1.2.6.1Выявление проблемы — анализ ее существования
- •1.2.6.2Постановка проблемы
- •1.2.6.3Поиск решения проблемы
- •1.2.6.4Принятие решения
- •1.2.6.5Исполнение решения
- •1.2.6.6Оценка выполненного решения
- •1.3Формализм теории исследования операций (модель операции)
- •1.4Оценка эффективности стратегии
- •1.4.1Оценка неопределенности стратегии
- •1.4.2Функциональная оптимизация стратегий
- •1.4.3Смешанные стратегии
- •Лекция № 2.Моделирование целевых установок в сложных системах (2 ч.)
- •2.1Классификация целей систем
- •2.2Графы целей и способы их построения
- •2.3Методы свертки показателей эффективности
- •2.3.1.1Экономический способ формирования критериев
- •2.3.1.2Критические состояния объекта
- •2.3.1.3Последовательное достижение частных целей
- •2.3.1.4Логическое объединение критериев
- •2.3.1.5Обобщенное логическое объединение
- •2.3.1.6Случайное и неопределенное объединение
- •2.3.1.7Единицы измерения целей
- •2.3.1.8Полнота системы элементарных действий над критериями
- •2.4Экспертная оценка эффективности
- •2.5Критерии эффективности организационного управления
- •Лекция № 3. Примеры моделей операций (2 ч.)
- •3.1Модель анализа технологических процессов
- •3.2Аппроксимация функций полиномами
- •3.3Модель численного поиска экстремума
- •3.4Модель действий нападения против защиты в военных операциях
- •3.5Модель производства продукции в условиях конкуренции
- •3.6Модель оценки надежности неремонтируемых систем
- •3.6.1Параллельное дублирование системы в целом
- •3.6.2«Холодное резервирование» системы в целом
- •3.6.3Параллельное дублирование агрегатов системы
- •3.6.4«Холодное резервирование» агрегатов
- •3.7Модель для выбора дальности стрельбы в дуэльной ситуации
- •3.8Линейная обработка измерений (фильтрация) координат движущихся объектов
- •3.8.1Случайное блуждание координат движущегося объекта
- •3.8.2Зависимое блуждание координат движущегося объекта
- •3.8.3Ограниченное блуждание координат движущегося объекта
- •Лекция № 4.Элементы выпуклого анализа
- •4.1Вспомним основные понятия высшей алгебры
- •4.2Определение и примеры выпуклых множеств.
- •-Мерный куб с центром в точке и ребром :
- •-Мерный шар радиуса с центром в точке :
- •4.3Проекция точки на множество. Свойства.
- •4.4Теоремы отделимости выпуклых множеств.
- •4.5Крайние точки выпуклых множеств.
- •4.6Альтернативы Фредгольма.
- •4.7Выпуклые функции и их свойства.
- •4.8Связь между выпуклыми функциями и выпуклыми множествами
- •4.9Свойства выпуклых функций.
- •4.9.1Дифференцируемость скалярной выпуклой функции.
- •4.9.2Дифференцируемость по направлению.
- •4.9.3Непрерывность.
- •4.10Выпуклые дифференцируемые функции и их экстремальные свойства
- •4.11Критерии оптимальности
- •Лекция № 5.Основы выпуклого программирования. Теория Куна-Таккера
- •5.1Основная задача выпуклого программирования
- •5.2Формальная постановка задачи выпуклого программирования
- •5.3 Классические способы отыскания решения экстремальных задач
- •5.4Условие регулярности
- •5.5Функция Лагранжа. Условия оптимальности
- •5.6Теорема (Куна-Таккера).
- •5.7Дифференциальные условия Куна-Таккера
- •5.8Общая схема решения задачи выпуклого программирования
- •Лекция № 6.Линейное программирование
- •6.1Примеры моделей операций, приводящих к злп
- •6.1.1Задача о диете
- •6.1.2Общая задача планирования выпуска продукции (распределительная задача)
- •6.1.2.1Общая задача планирования выпуска продукции
- •6.1.2.2Выпуск комплектной продукции
- •6.1.3Транспортная задача
- •6.1.3.1Классическая транспортная задача
- •6.1.3.2Транспортная задача с фиксированными доплатами
- •6.2Различные виды злп и их эквивалентность
- •6.2.1Стандартная задача линейного программирования
- •Лекция № 7. Игровые методы обоснования решений
- •7.1Теория игр как теория обоснования решений в условиях конфликта интересов
- •7.2Конфликт и его формальная модель
- •7.3Формализация принятия решения в условиях конфликта
- •7.4Оптимальность в конфликтной ситуации
5.3 Классические способы отыскания решения экстремальных задач
Вспомним, какие алгоритмы поиска экстремума функции нам известны.
Рассмотрим простейшую
задачу о поиске минимума дифференцируемой
функции на отрезке. Пусть
![]() — скалярная функция скалярного аргумента
— скалярная функция скалярного аргумента
![]() ,
заданная на отрезке
,
заданная на отрезке
![]() .
Требуется найти минимальное значение
на
.
Алгоритм, который дает для решения этой
задачи классический математический
анализ заключается в следующем:
.
Требуется найти минимальное значение
на
.
Алгоритм, который дает для решения этой
задачи классический математический
анализ заключается в следующем:
вычислить производную
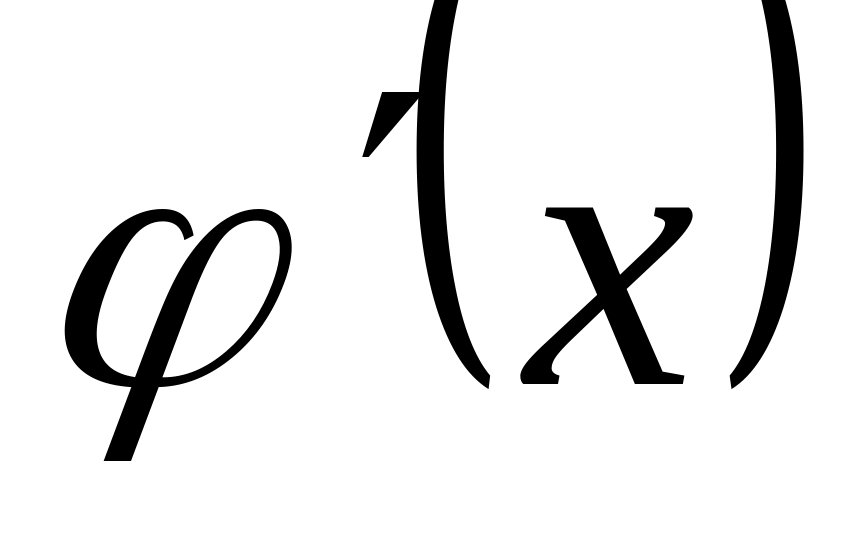 ;
;найти все решения
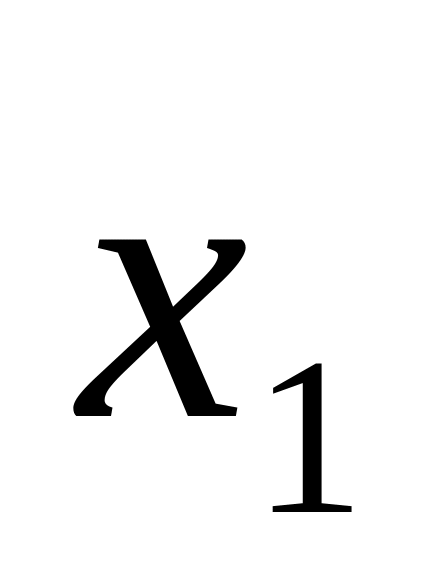 ,
,
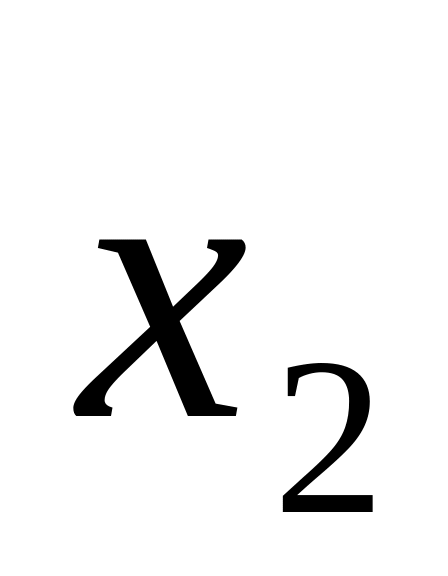 ,...,
,...,
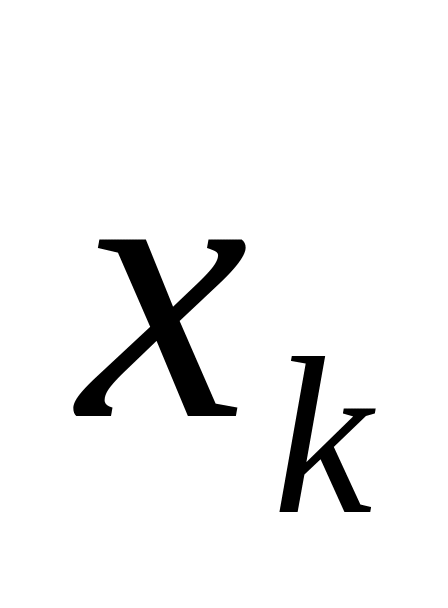 уравнения
=0
(стационарные точки);
уравнения
=0
(стационарные точки);вычислить значения
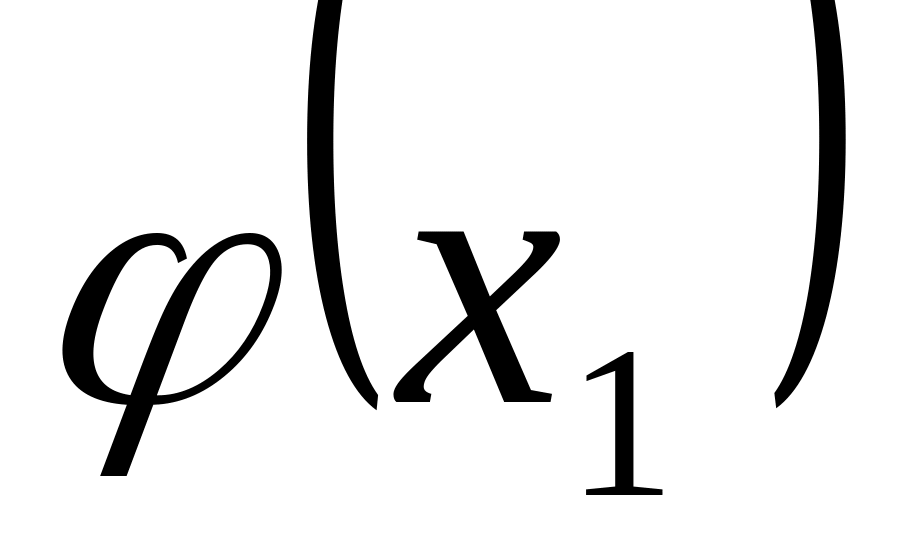 ,
,
 ,...,
,...,
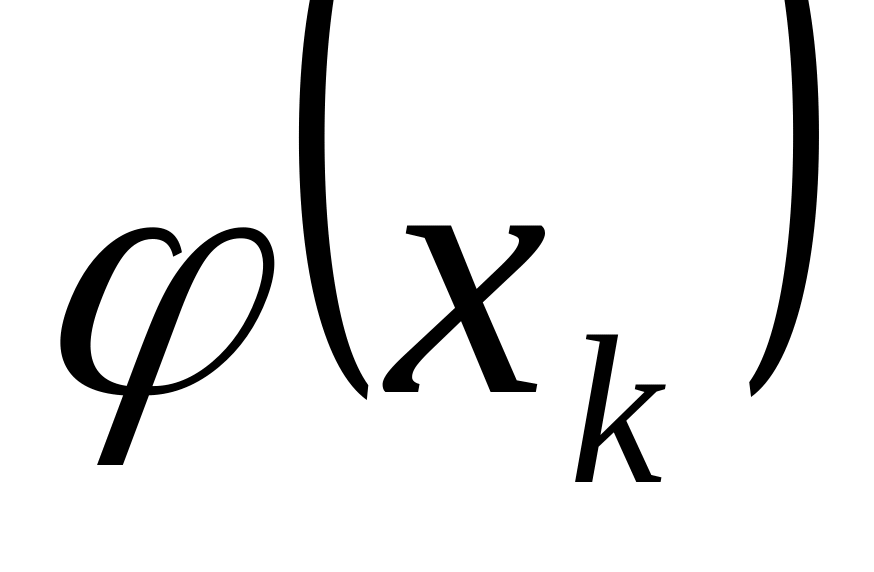 ,
,
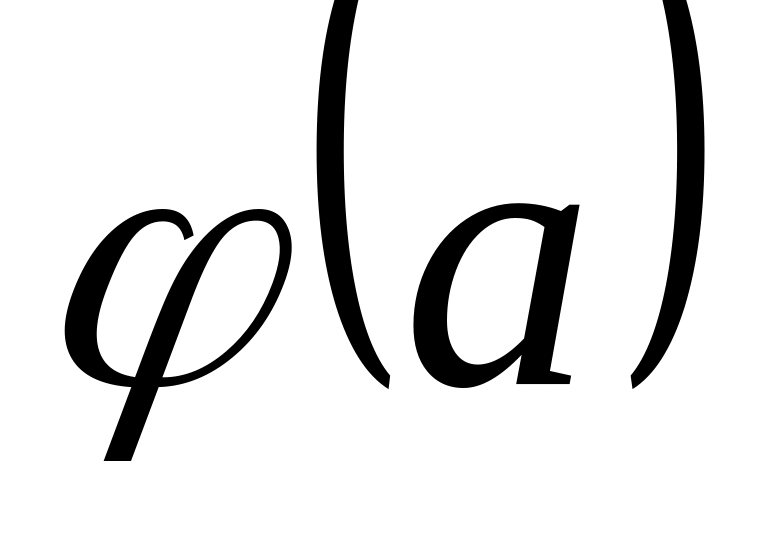 ,
,
 ;
;выбрать среди этих значений минимальное.
Уже в простейшем случае возникает ряд вопросов. Как решать уравнение =0: не будет ли эта задача столь же сложна, как и основная проблема поиска экстремума? Что делать, если стационарных точек , ,..., очень много, или даже бесконечное многожество? Как организовать перебор и сравнение значений?
Еще сложнее обстоит дело с функциями нескольких переменных. Пусть — замкнутое подмножество , — функция переменных, заданная на множестве . Для того чтобы найти минимальное значение на множестве , классический математический анализ рекомендует
найти все решения ,
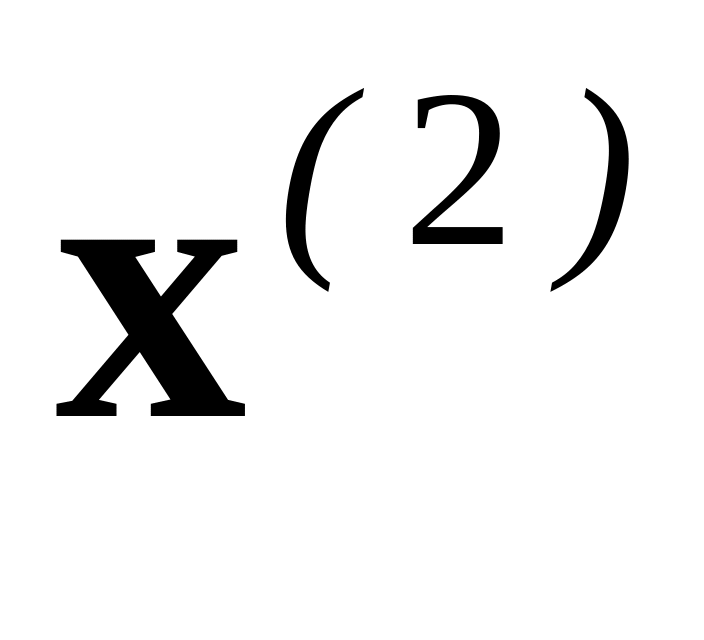 ,...,
,...,
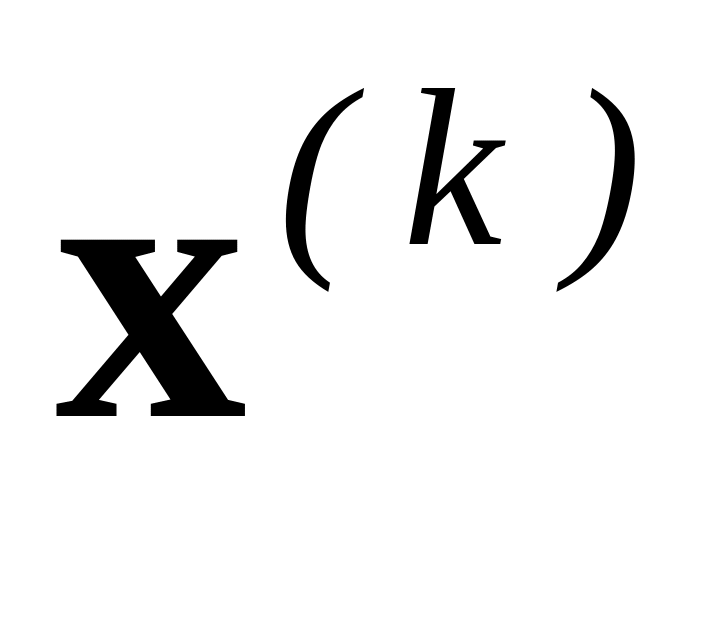 уравнения
уравнения
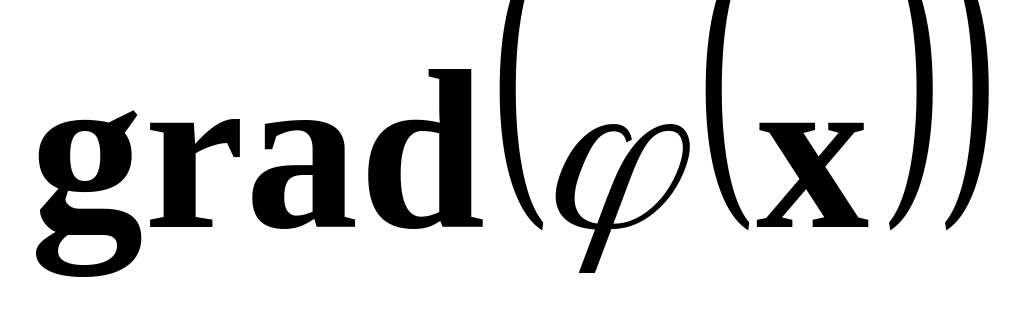 =0;
=0;вычислить значения функции в этих точках;
вычислить все значения в границе множества ;
выбрать из указанных значений максимальное.
Очевидно, что даже если удается легко выполнить пп. 1, 2, то выполнить п. 3 практически невозможно. Таким образом, классический математический анализ не дает общего рецепта — для каждой задачи необходимо искать собственный метод решения. В задачах о поиске экстремума функции на некотором множестве , заданном системой равенств, наиболее распространенный метод исследования — метод множителей Лагранжа — состоит в отыскании стационарных точек функции Лагранжа.
Как поступают в классическом случае, например для следующей задачи: найти максимальное значение функции
![]() =
=![]()
на
множестве
={![]() }?
}?
Для решения задачи строят функцию Лагранжа
![]() =
+
=
+![]() .
.
Затем отыскивают точки безусловного экстремума как стационарные точки функции Лагранжа:
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() .
.
Решая полученную
систему уравнений, находим искомые
значения оптимального плана
![]() ,
,
![]() ,
значение задачи
=
,
значение задачи
=![]() ,
а также число
,
а также число
![]() ,
называемое множителем Лагранжа.
,
называемое множителем Лагранжа.
5.4Условие регулярности
Будем предполагать,
что для задачи выпуклого программирования
справедливо следующее условие: для
каждого
существует такая точка
,
что
![]() (
).
Это условие эквивалентно следующему,
которое принято называть условие
регулярности Слейтера: существует
такая точка
,
что
>
.
(
).
Это условие эквивалентно следующему,
которое принято называть условие
регулярности Слейтера: существует
такая точка
,
что
>
.
Доказать эквивалентность двух условий регулярности.
5.5Функция Лагранжа. Условия оптимальности
Рассмотрим
-мерный
вектор
![]() =
.
=
.
Функцию
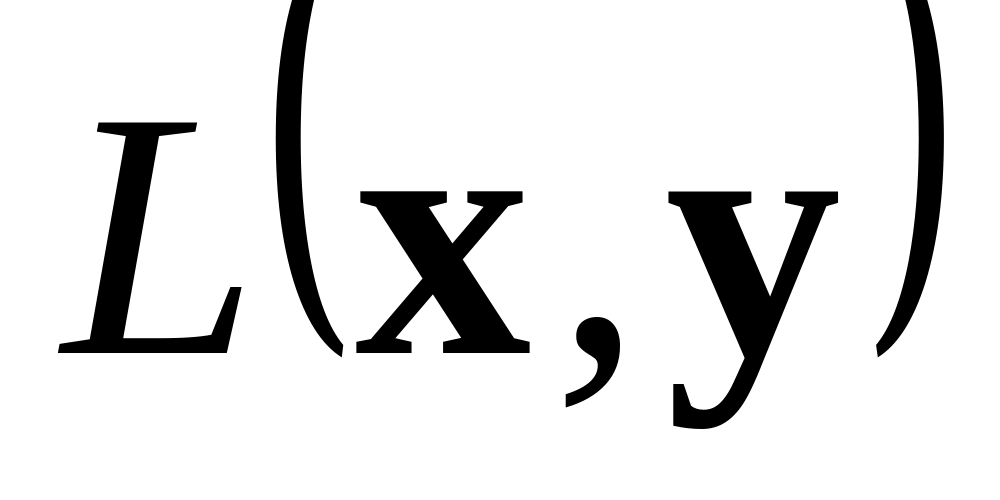 =
+<
,
>,
где
=
+<
,
>,
где
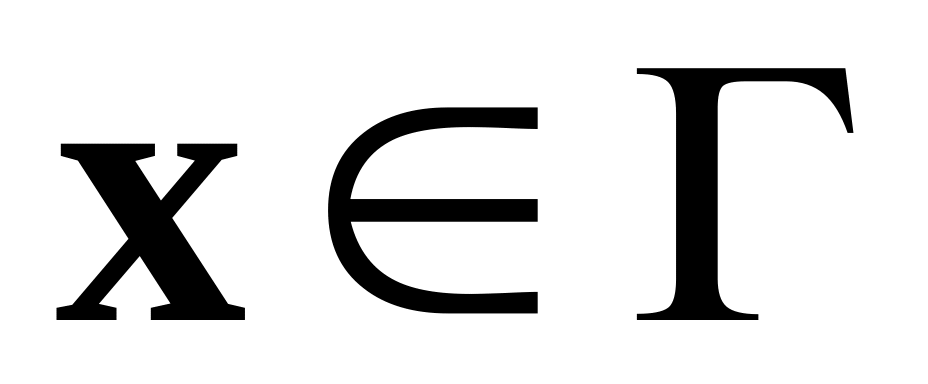 ,
вектор
,
называют функцией Лагранжа основной
задачи выпуклого программирования.
,
вектор
,
называют функцией Лагранжа основной
задачи выпуклого программирования.Седловой точкой функции на множестве ,
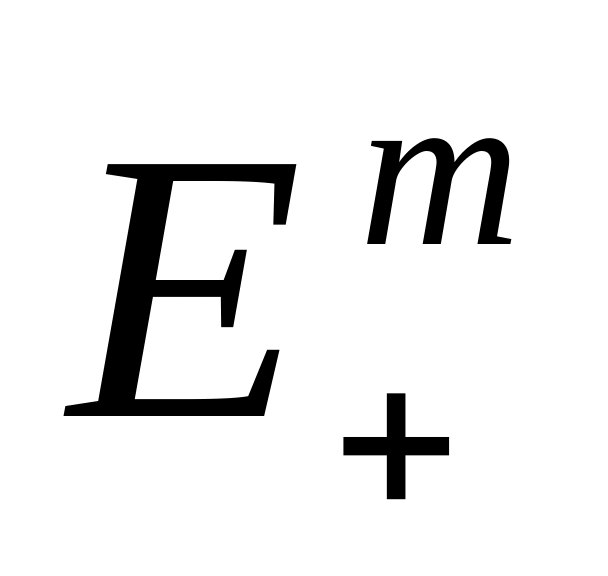 ,
называется пара (
,
,
называется пара (
, )
)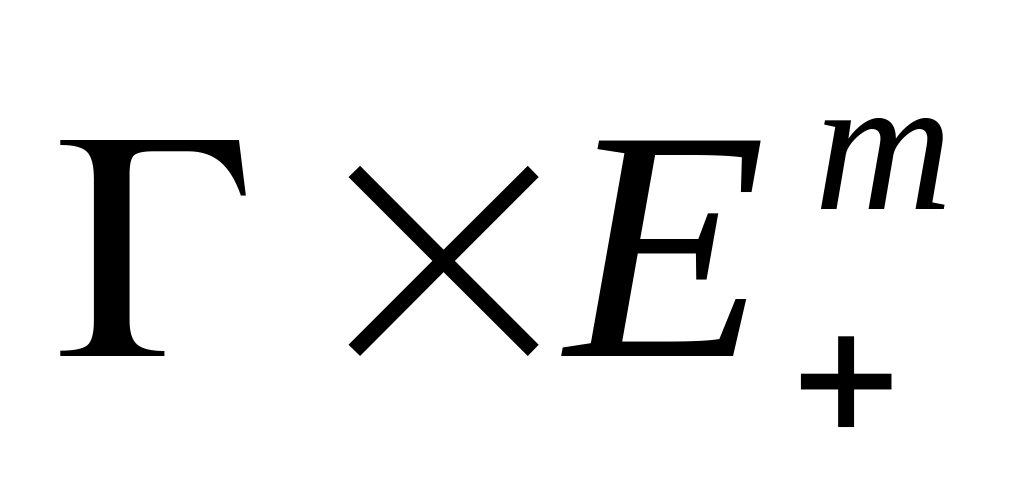 ,
что для всех
,
выполнено
,
что для всех
,
выполнено
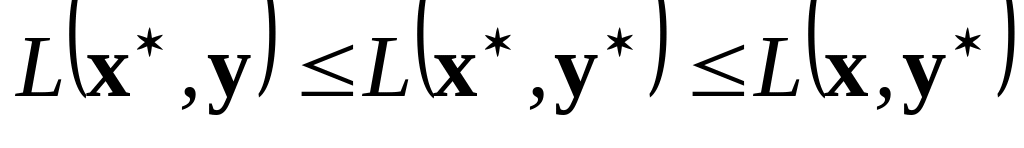 .
.
(105) можно записать в виде:
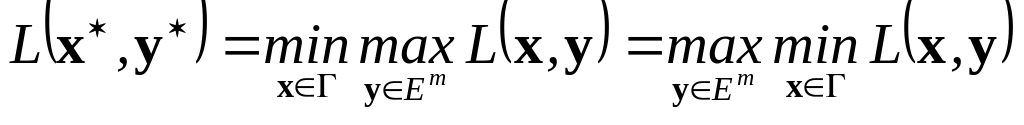 .
.
Последнее соотношение часто используется в теории матричных игр и характеризует седловую точку рассматриваемой игры: минимакс равен максимину.
(о достаточных условиях оптимальности задачи выпуклого программирования). Если пара ( , ) является седловой точкой функции Лагранжа на множестве , , то — оптимальная точка основной задачи выпуклого программирования (102).
ДОКАЗАТЕЛЬСТВО. Из определения функции Лагранжа и (105) получим:
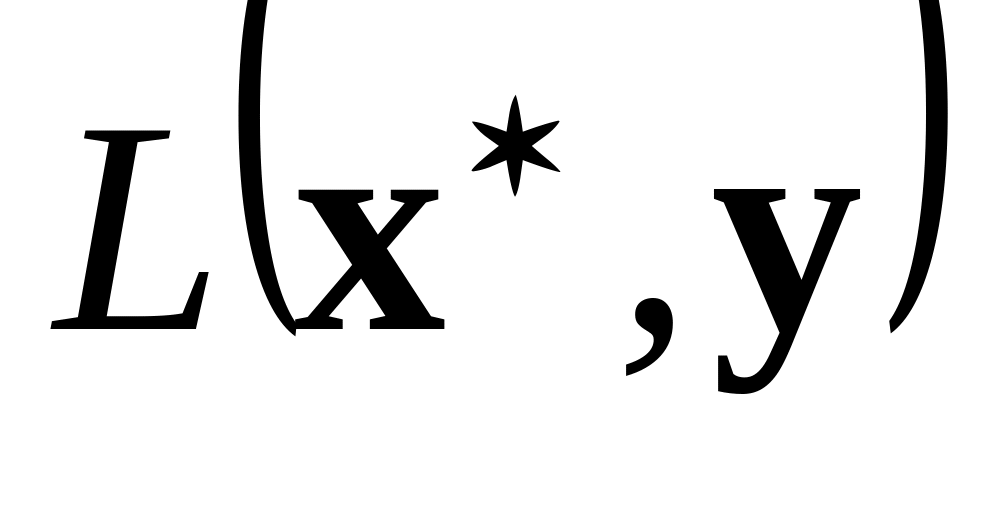 =
+<
,
=
+<
,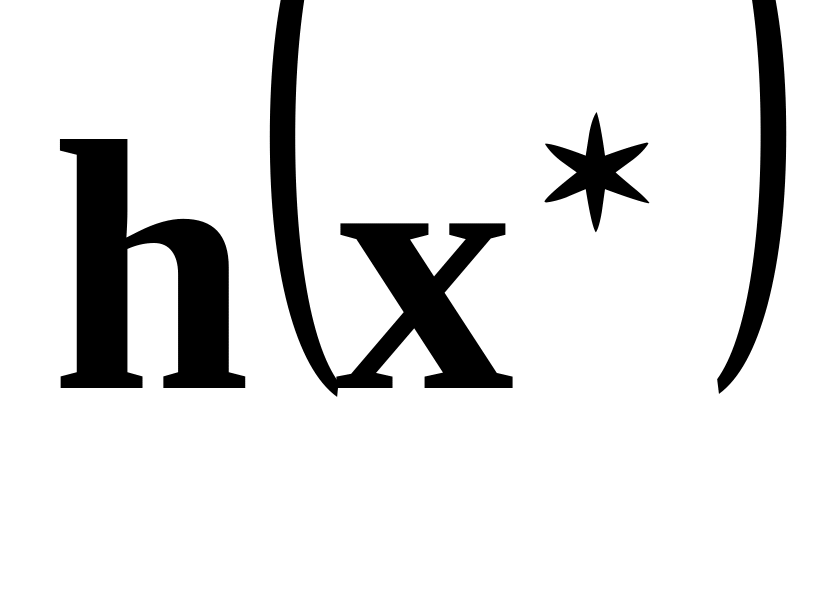 >
+<
,
>
+<
,
>.
>
+<
,
>
+<
,
>.
Из левого неравенства следует, что для любого
< , >< , >,
а поскольку и это неравенство справедливо для любого ,то 0.
В частности, при =0 имеем: < , >=0. Если , то по определению 0, поэтому для всех будет
< , >0.
Поскольку (107) справедливо и для всякого , то получаем для всех :
> +< , > .
Так как
(ибо
![]() и
0),
то получаем, что допустимый план
является оптимальным.
и
0),
то получаем, что допустимый план
является оптимальным.
