
Задача № 3
Человек, проходящий мимо киоска, покупает газету с вероятностью 0,2. Найти вероятность того, что из 400 человек, прошедших мимо киоска в течение часа:
а) купят газету 90 человек;
б) не купят газету от 300 до 340 человек (включительно).
Решение.
Здесь мы имеем дело с независимыми
испытаниями, каждое из которых заключается
в прохождении мимо киоска человека.
Число испытаний в нашем случае
![]() .
.
а) Вычислить искомую вероятность
![]() появления события ровно 90 раз в 400
испытаниях по формуле Бернулли
затруднительно из-за громоздкости
вычислений. Искомую вероятность
можно вычислить, используя асимптотическую
(приближённую) формулу Муавра – Лапласа.
появления события ровно 90 раз в 400
испытаниях по формуле Бернулли
затруднительно из-за громоздкости
вычислений. Искомую вероятность
можно вычислить, используя асимптотическую
(приближённую) формулу Муавра – Лапласа.
Воспользуемся локальной теоремой Муавра – Лапласа:
если вероятность
наступления события
в каждом из испытаний постоянна и
отлична от 0 и 1, а число независимых
испытаний достаточно велико, то
вероятность
![]() вычисляется по приближённой формуле
вычисляется по приближённой формуле
![]() ,
где
,
где
– вероятность наступления события в каждом из испытаний,
– вероятность ненаступления события в каждом из испытаний,
![]() – функция Гаусса.
– функция Гаусса.
Пусть событие
состоит в том, что человек, проходящий
мимо киоска, покупает газету; вероятность
наступления события
в каждом из испытаний
![]() ;
вероятность ненаступления события в
каждом из испытаний
;
вероятность ненаступления события в
каждом из испытаний
![]() ;
число испытаний
.
;
число испытаний
.
Значит вероятность того, что из 400 человек, прошедших мимо киоска в течение часа, купят газету 90 человек:
![]() .
.
По таблице значений функции Гаусса
находим:
![]() .
.
Следовательно,
![]() .
.
б) Воспользуемся интегральной теоремой Муавра – Лапласа:
вероятность того, что событие
появится в
независимых испытаниях от
![]() до
до
![]() раз вычисляется по формуле
раз вычисляется по формуле
![]() ,
где
,
где
– вероятность наступления события в каждом из испытаний,
– вероятность ненаступления события в каждом из испытаний,
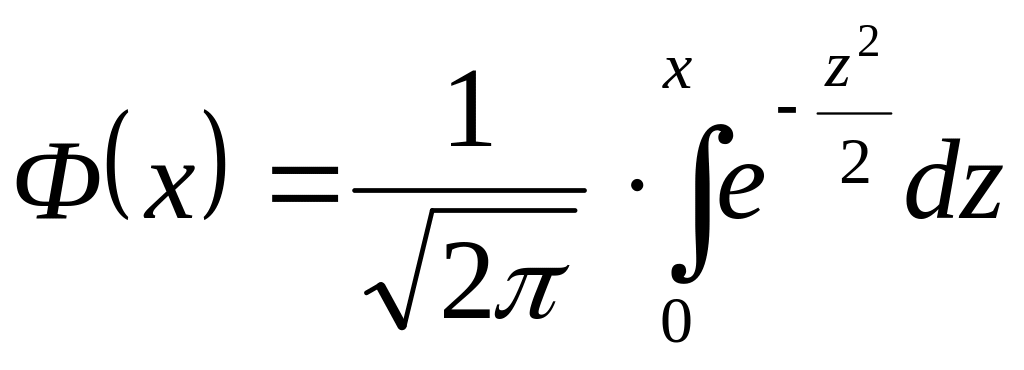 – функция Лапласа.
– функция Лапласа.
Пусть событие
состоит в том, что человек, проходящий
мимо киоска, не покупает газету;
вероятность наступления события
в каждом из испытаний
![]() ;
вероятность ненаступления события в
каждом из испытаний
;
вероятность ненаступления события в
каждом из испытаний
![]() ;
число испытаний
;
;
число испытаний
;
![]() ,
,
![]() .
.
Значит вероятность того, что из 400 человек, прошедших мимо киоска в течение часа, не купят газету от 300 до 340 человек (включительно):
![]()
![]() .
.
По таблице значений функции Лапласа
находим:
![]() .
.
Следовательно,
![]() .
.
Ответ:
а)
![]() ;
б)
;
б)
![]() .
.
Задача № 4
Пульт охраны связан с тремя охраняемыми объектами. Вероятность поступления сигнала с этих объектов составляет 0,2; 0,3 и 0,6 соответственно. Составить закон распределения случайной величины – числа объектов, с которых поступит сигнал. Найти математическое ожидание и дисперсию этой случайной величины.
Решение.
Дискретная случайная величина
![]() – число объектов, с которых поступит
сигнал, – имеет следующие возможные
значения:
– число объектов, с которых поступит
сигнал, – имеет следующие возможные
значения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найдём вероятности
![]() ,
,
![]() ,
,
![]() ,
,
![]() этих возможных значений.
этих возможных значений.
Х |
|
|
|
|
Р |
|
|
|
|
величины , соответственно, будет иметь вид:
Обозначим:
![]() – событие, которое заключается в том,
что с 1-ого объекта поступил сигнал;
– событие, которое заключается в том,
что с 1-ого объекта поступил сигнал;
![]() – событие, которое заключается в том,
что со 2-ого объекта поступил сигнал;
– событие, которое заключается в том,
что со 2-ого объекта поступил сигнал;
![]() – событие, которое заключается в том,
что с 3-его объекта поступил сигнал.
– событие, которое заключается в том,
что с 3-его объекта поступил сигнал.
По условию:
![]() ;
;
![]() ;
;
![]() .
.
Событие
![]() ,
противоположное событию
,
состоит в том, что с 1-ого объекта не
поступил сигнал;
,
противоположное событию
,
состоит в том, что с 1-ого объекта не
поступил сигнал;
![]() .
.
Событие
![]() ,
противоположное событию
,
состоит в том, что со 2-ого объекта
не поступил сигнал;
,
противоположное событию
,
состоит в том, что со 2-ого объекта
не поступил сигнал;
![]() .
.
Событие
![]() ,
противоположное событию
,
состоит в том, что с 3-его объекта не
поступил сигнал;
,
противоположное событию
,
состоит в том, что с 3-его объекта не
поступил сигнал;
![]() .
.
Число объектов, с которых поступит сигнал, только в случае совместного появления событий , и . Поэтому, учитывая независимость событий , и , по теореме умножения вероятностей получаем:
![]() .
.
Число объектов, с которых поступит
сигнал,
в случаях совместного появления либо
событий
,
и
,
либо событий
,
и
,
либо событий
,
и
.
Поэтому, учитывая несовместность
событий
![]() ,
,
![]() и
и
![]() ,
по теореме сложения вероятностей
получаем:
,
по теореме сложения вероятностей
получаем:
![]()
![]()
![]()
![]() .
.
(здесь мы также применили теорему умножения вероятностей, учитывая независимость событий , и ).
Число объектов, с которых поступит
сигнал,
в случае совместного появления либо
событий
,
и
,
либо событий
,
и
,
либо событий
,
и
.
Поэтому, учитывая несовместность
событий
![]() ,
,
![]() и
и
![]() ,
по теореме сложения вероятностей
получаем:
,
по теореме сложения вероятностей
получаем:
![]()
![]()
![]()
![]() .
.
(здесь мы также применили теорему умножения вероятностей, учитывая независимость событий , и ).
Число объектов, с которых поступит
сигнал,
![]() только в случае совместного появления
событий
,
и
.
Поэтому, учитывая независимость
событий
,
и
,
по теореме умножения вероятностей
получаем:
только в случае совместного появления
событий
,
и
.
Поэтому, учитывая независимость
событий
,
и
,
по теореме умножения вероятностей
получаем:
![]() .
.
Сумма вероятностей
![]() .
.
Таким образом, искомый закон распределения дискретной случайной величины
|
0 |
1 |
2 |
3 |
|
0,224 |
0,488 |
0,252 |
0,036 |
Вычислим числовые характеристики случайной величины (параметры распределения):
Математическое ожидание дискретной случайной величины :
![]() .
.
Дисперсия дискретной случайной величины :
![]() ,
где
,
где
![]() .
.
![]() ,
значит
,
значит
![]() .
.
|
0 |
1 |
2 |
3 |
|
0,224 |
0,488 |
0,252 |
0,036 |
