
Контрольная работа по теории вероятности №3 Вариант 3. Выполнено авторским коллективом ООО «Взфэи-архив.рф» © 2010. Avzfei.ru. Авторские права на данную работу зарегистрированы Российским авторским обществом КОПИРУС совместно с Федеральным государственным учреждением Российская государственная библиотека - РГБ.
© ООО «ВЗФЭИ-АРХИВ.РФ», 2010
Электронная версия данного текстовой работы предназначена исключительно для ознакомления. Незаконное распространение, публикация (в том числе и на интернет-ресурсах), передача третьим лицам текста данной работы, либо фрагментов текста данной работы без прямой цитаты и согласования с правообладателем преследуется по закону, а лица виновные в данных правонарушениях несут ответственность, предусмотренную главой 4 Гражданского Кодекса РФ.
Если Вы обнаружили данную работу на каком-либо сайте, кроме avzfei.ru, взфэи.su, взфэи-архив.рф – немедленно сообщите об этом на адрес электронной почты: vzfeiextra@ya.ru – Вознаграждение сообщившему гарантируется!
Контрольная работа № 3
Вариант 5
Задача № 1
Ребёнок играет
кубиками, на которых написаны буквы:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() .
Найти вероятность того, что произвольно
поставленные в ряд пять букв образуют
слово «ШАРИК».
.
Найти вероятность того, что произвольно
поставленные в ряд пять букв образуют
слово «ШАРИК».
Решение.
Испытание (опыт) заключается в выборе по одному пяти кубиков с буквами в случайном порядке без возврата.
Элементарным событием (исходом испытания) является полученная последовательность из пяти букв. Элементарные события являются размещениями из 7 букв ( , , , , , , ) по 5 букв.
Число всех возможных исходов испытания:
![]() .
.
Пусть событие заключается в том, что буквы выбраны в порядке заданного слова «ШАРИК».
Число исходов, благоприятствующих появлению события , соответствует числу всех возможных использований букв Ш, А, Р, И и К, входящих в слово «ШАРИК»:
![]() .
.
Воспользовавшись классическим определением вероятности, получаем:
![]() .
.
Ответ:
![]() .
.
Задача № 2
При тестировании качества радиодеталей установлено, что на каждые 10000 радиодеталей в среднем приходится четыре бракованных. Определить вероятность того, что при проверке 5000 радиодеталей будет обнаружено:
а) не менее трёх бракованных деталей;
б) не менее одной и не более трёх бракованных деталей.
Решение.
Здесь мы имеем дело с независимыми
испытаниями, каждое из которых заключается
в тестировании качества радиодетали.
Число испытаний в нашем случае
![]() .
.
В нашем случае событие состоит в том, что деталь является бракованной.
а) Вероятность обнаружения при проверке
5000 радиодеталей не менее трёх бракованных
деталей равна
![]() .
.
Вычислить искомые вероятности
![]() ,
,
![]() ,
,
![]() появления события в 5000 испытаниях
по формуле Бернулли
появления события в 5000 испытаниях
по формуле Бернулли
![]() затруднительно из-за громоздкости
вычислений. Искомую искомые вероятности
,
,
можно вычислить, используя асимптотические
(приближённые) формулы Пуассона и
Муавра – Лапласа.
затруднительно из-за громоздкости
вычислений. Искомую искомые вероятности
,
,
можно вычислить, используя асимптотические
(приближённые) формулы Пуассона и
Муавра – Лапласа.
Воспользуемся теоремой Пуассона:
если вероятность
![]() наступления события
в каждом испытании постоянна и мала
наступления события
в каждом испытании постоянна и мала
![]() ,
число испытаний
,
число испытаний
![]() – велико
– велико
![]() и число
и число
![]() – незначительно
– незначительно
![]() ,
то вероятность
,
то вероятность
![]() того, что событие
появится
того, что событие
появится
![]() раз в
независимых испытаниях вычисляется
по приближённой формуле
раз в
независимых испытаниях вычисляется
по приближённой формуле
![]() ,
где
,
где
![]() – функция Пуассона.
– функция Пуассона.
В нашем случае вероятность появления
события
![]() постоянна и мала, число независимых
испытаний
велико, число
постоянна и мала, число независимых
испытаний
велико, число
![]() .
.
Значит вероятность появления события не менее 3 раз в 5000 испытаниях:
![]() .
.
По таблице значений функции Пуассона находим:
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, вероятность обнаружения при проверке 5000 радиодеталей не менее трёх бракованных деталей равна
![]() .
.
б) Вероятность обнаружения при проверке
5000 радиодеталей не менее одной и не
более трёх бракованных деталей равна
![]() .
.
Снова воспользуемся теоремой Пуассона:
если вероятность наступления события в каждом испытании постоянна и мала , число испытаний – велико и число – незначительно , то вероятность того, что событие появится раз в независимых испытаниях вычисляется по приближённой формуле , где – функция Пуассона.
В нашем случае вероятность появления события постоянна и мала, число независимых испытаний велико, число .
Значит вероятность появления события не менее 1 и не более 3 раз в 5000 испытаниях:
![]() .
.
По таблице значений функции Пуассона находим:
,
,
![]() .
.
Следовательно, вероятность обнаружения при проверке 5000 радиодеталей не менее одной и не более трёх бракованных деталей равна
![]() .
.
Ответ:
а)
![]() ;
б)
;
б)
![]() .
.
Задача № 3
Вероятность гибели саженца составляет 0,4. Составить закон распределения числа прижившихся саженцев из имеющихся четырёх. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и функцию распределения этой случайной величины.
Решение.
Дискретная случайная величина Х
– число прижившихся саженцев – имеет
следующие возможные значения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найдём вероятности
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() этих возможных значений.
этих возможных значений.
Х |
|
|
|
|
|
Р |
|
|
|
|
|
величины Х, соответственно, будет иметь вид:
Пусть – событие, которое заключается в том, что саженец погиб.
Так как число испытаний невелико, то
для вычисления искомых вероятностей
воспользуемся формулой Бернулли
![]() ,
где
,
где
![]() – число сочетаний из
элементов по
;
– число сочетаний из
элементов по
;
– вероятность появления события
в каждом из испытаний, по условию
![]() ;
;
![]() – вероятность непоявления события
в каждом из испытаний,
– вероятность непоявления события
в каждом из испытаний,
![]() .
.
Число прижившихся саженцев
возможно только в случае появления
события
ровно 4 раза в
![]() испытаниях. Поэтому
испытаниях. Поэтому
![]() .
.
Число прижившихся саженцев возможно только в случае появления события ровно 3 раза в испытаниях. Поэтому
![]() .
.
Число прижившихся саженцев возможно только в случае появления события ровно 2 раза в испытаниях. Поэтому
![]() .
.
Число прижившихся саженцев возможно только в случае появления события ровно 1 раз в испытаниях. Поэтому
![]() .
.
Число прижившихся саженцев возможно только в случае появления события ровно 0 раз в испытаниях. Поэтому
![]() .
.
Сумма вероятностей
![]() .
.
Таким образом, искомый закон распределения дискретной случайной величины Х
Х |
0 |
1 |
2 |
3 |
4 |
Р |
|
|
|
|
|
Вычислим числовые характеристики случайной величины Х (параметры распределения):
Математическое ожидание дискретной случайной величины Х:
![]()
![]()
![]() .
.
Дисперсия дискретной случайной величины
Х:
![]() ,
где
,
где
![]() .
.
![]()
![]() ,
,
значит
![]() .
.
Среднее квадратическое отклонение
![]() .
.
Функция распределения вероятностей
(интегральная функция распределения)
![]() случайной величины
случайной величины
![]() задаётся формулой
задаётся формулой
![]() .
.
При построении функции будем получать её аналитическое выражение на каждом промежутке разбиения числовой прямой точками, соответствующими значениям заданной случайной величины, используя теорему сложения вероятностей несовместных событий:
для

 ,
так как в данном случае мы имеем дело
с вероятностью невозможного события
(в частности для
,
так как в данном случае мы имеем дело
с вероятностью невозможного события
(в частности для

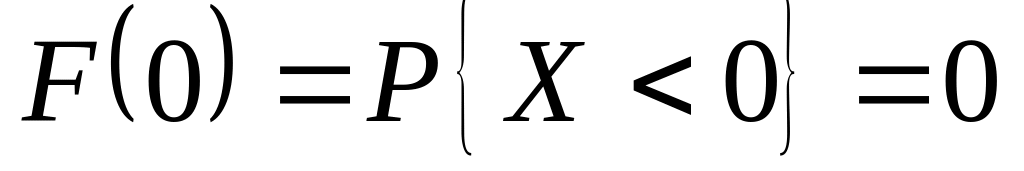 );
);
для
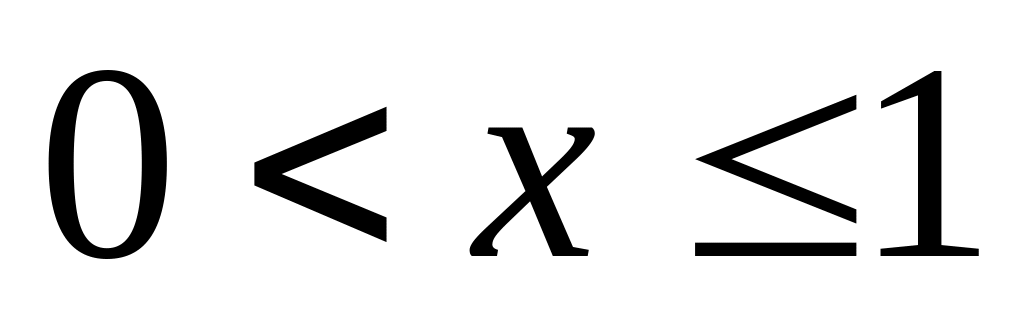
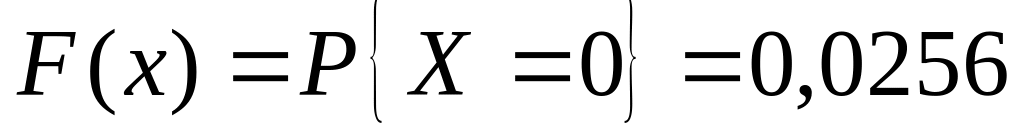 (в частности для
(в частности для
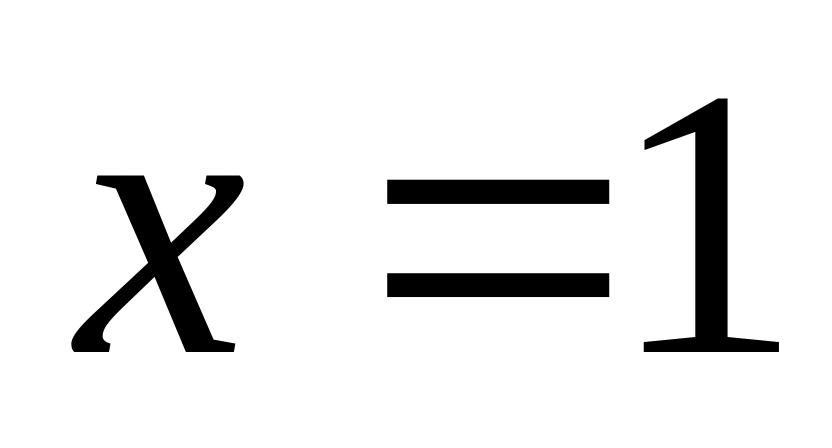
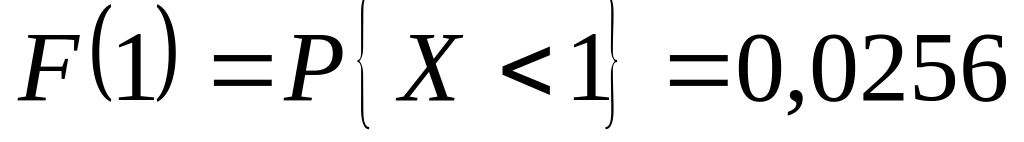 );
);
для

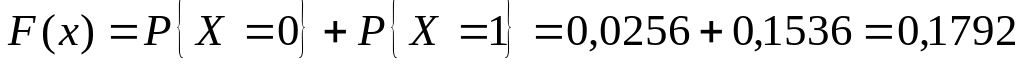 (в частности
для
(в частности
для
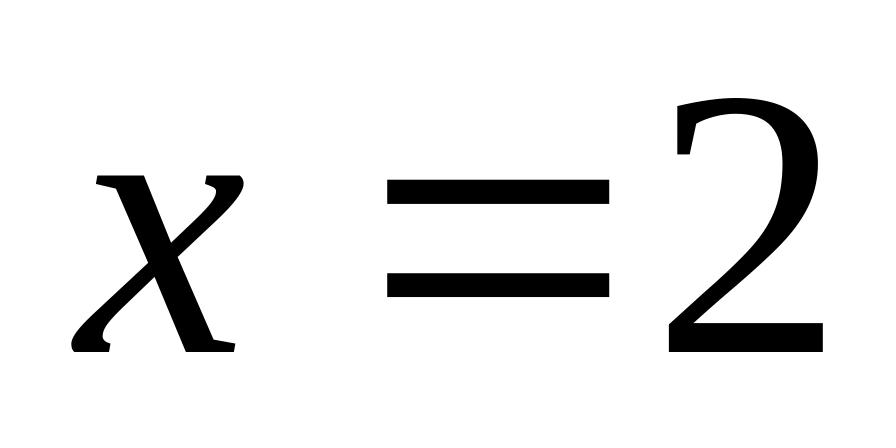
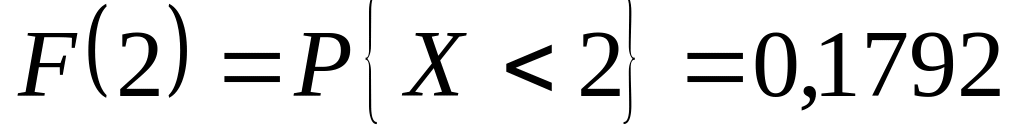 );
);
для
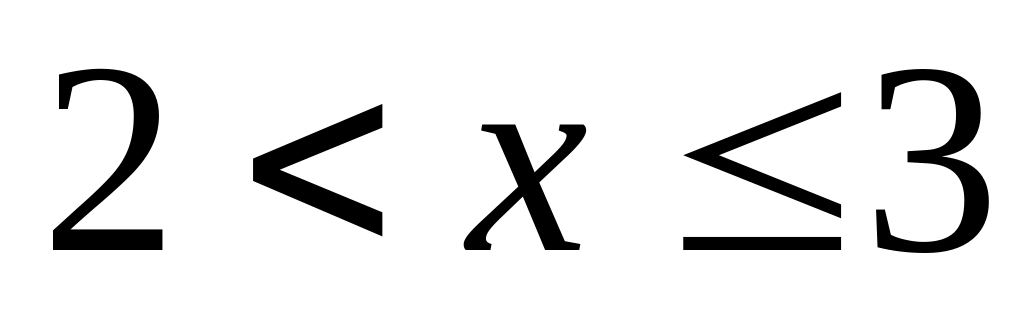
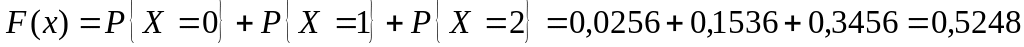 (в частности для
(в частности для
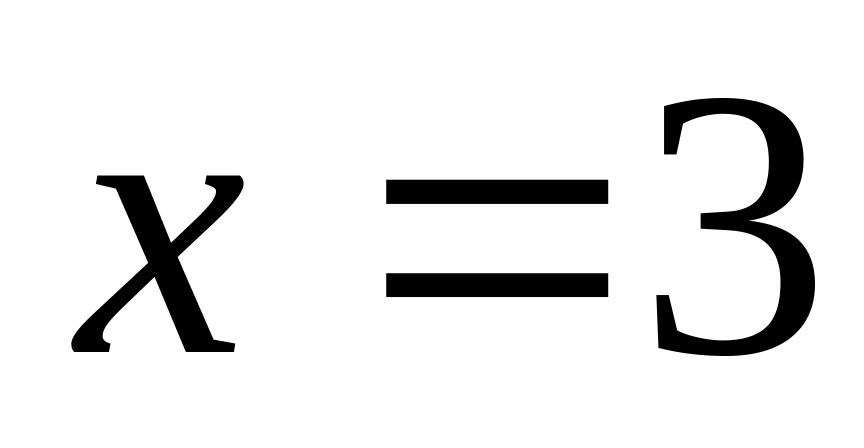
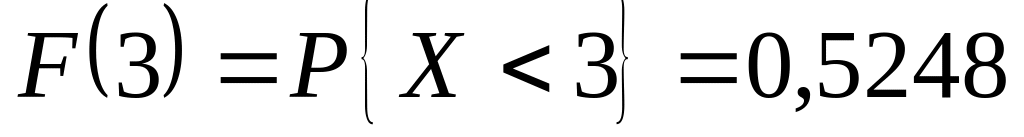 );
);
для
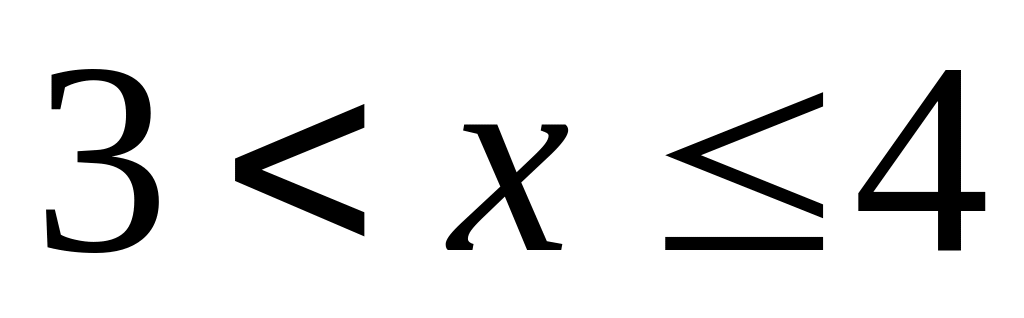

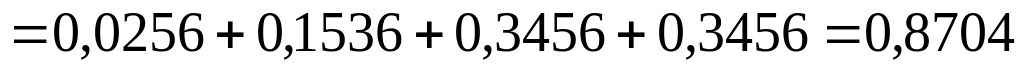
(в частности для
![]()
![]() );
);
для
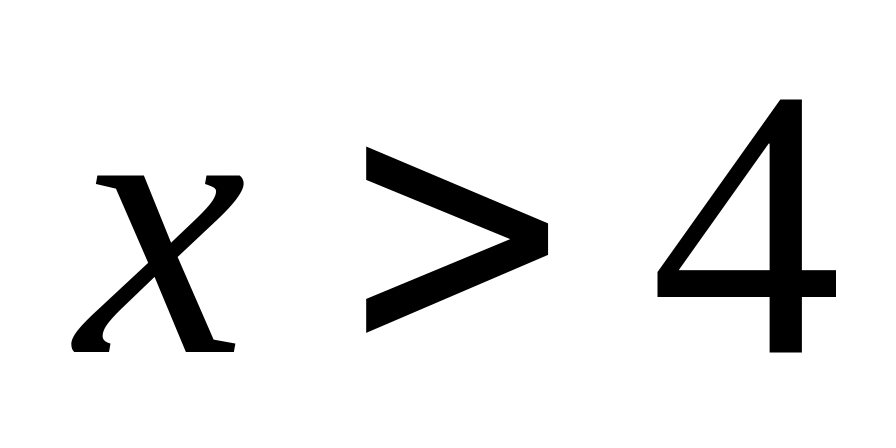
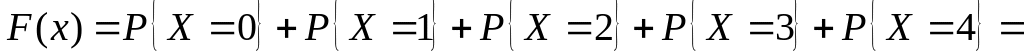
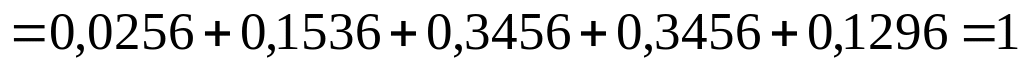 .
.
Обобщая полученные данные, можно
записать:
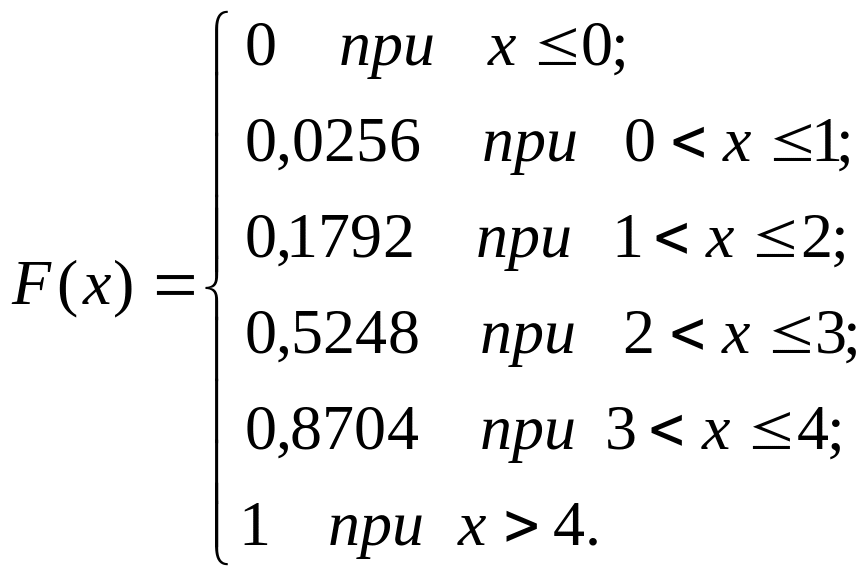
Х |
0 |
1 |
2 |
3 |
4 |
Р |
|
|
|
|
|
![]() ;
;
