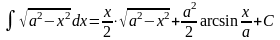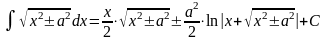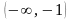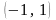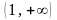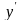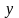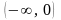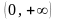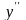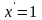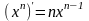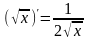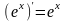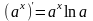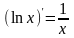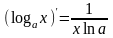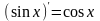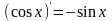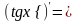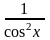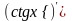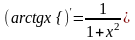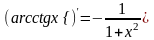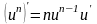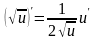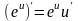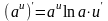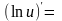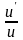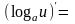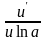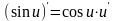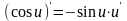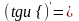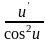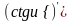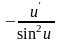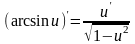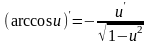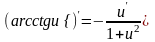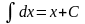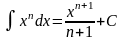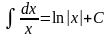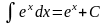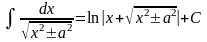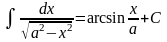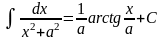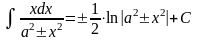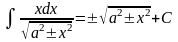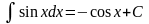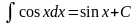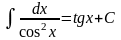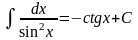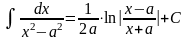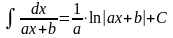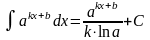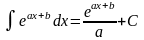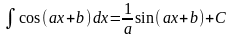- •Введение
- •Область применения методических указаний
- •1.2. Место учебной дисциплины в структуре основной профессиональной образовательной программы:
- •1.3. Цели и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины:
- •1.4. Количество часов на освоение рабочей программы учебной дисциплины:
- •2. Рабочая программа учебной дисциплины
- •2.1 Объем учебной дисциплины и виды учебной работы
- •2.2. Тематический план и содержание учебной дисциплины ен.01 Математика
- •Методические указания по каждой теме программы и вопросы для самоконтроля
- •Раздел 1.Основы математического анализа
- •Тема 1.1. Теория пределов. Непрерывность
- •Тема 1.2. Дифференциальное исчисление функции одной переменной
- •Тема 1.3.Интегральное исчисление функции одной переменной
- •Простейшие свойства определенного интеграла
- •Раздел 2. Обыкновенные дифференциальные уравнения
- •Тема 2.1. Дифференциальные уравнения 1 порядка
- •Линейные дифференциальные уравнения первого порядка
- •Тема 2.2. Дифференциальные уравнения2 порядка
- •Раздел 3. Ряды
- •Тема 3.1. Разложение функции в ряд
- •Раздел 4. Элементы аналитической геометрии
- •Тема 4.1. Прямая на плоскости. Кривые второго порядка
- •Тема 4.2. Прямоугольная система координат. Полярные координаты.
- •Раздел 5. Основы теории вероятностей
- •Тема 5.1. Элементы комбинаторики
- •Тема 5.2. Случайные события. Классическое определение вероятности.
- •Раздел 6. Случайные величины
- •Тема 6.1.Дискретная случайная величина.
- •Задание для контрольной работы
- •Примеры решения типовых заданий.
- •Контрольная работа «Основы математического анализа»
- •Перечень лабораторных работ и практических заданий
- •Контроль и оценка результатов освоения учебной дисциплины
Примеры решения типовых заданий.
Задание 1-20
Пример 1.
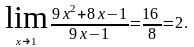
Пример 2.
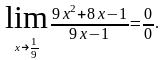
Здесь применима
теорема о пределе частного. К этому же
выражению при х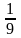 теорема о пределе неприменима, т. к.
теорема о пределе неприменима, т. к.
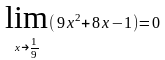 и
и
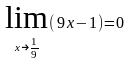 .
.
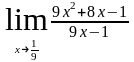 представляет собой неопределенность
вида
.
представляет собой неопределенность
вида
.
Разложим на множители квадратный трехчлен.
9х2+8х–1=9·(х– )·(х+1).Для этого достаточно найти корни х1 и х2 квадратного трехчлена
ах2+bх+с=а(х–х1)·(х–х2).
Под знаком предела сократим одинаковые множители и перейдем к пределу:
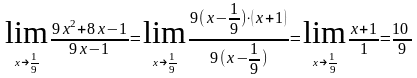
Пример 3.
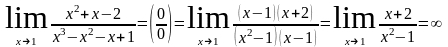 .
.
Обнаружив неопределенность (так это в примере и записывают), раскладываем многочлены в числителе и в знаменателе на множители.
Сократив
на х–1, получили дробь
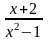 ,
числитель которой стремится к конечному
пределу, отличному от нуля (
,
числитель которой стремится к конечному
пределу, отличному от нуля (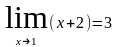 ),
а знаменатель при х1
является бесконечно малой, тогда дробь
при х1 является
бесконечно большой.
),
а знаменатель при х1
является бесконечно малой, тогда дробь
при х1 является
бесконечно большой.
Пример
4.
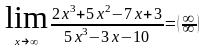 .
.
Решение. Здесь числитель и знаменатель не имеют конечных пределов, имеем неопределенность . Поделив одновременно числитель и знаменатель на х3, получим
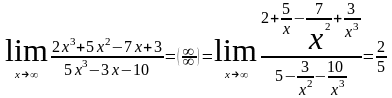 ,
т. к. каждая из дробей
,
т. к. каждая из дробей
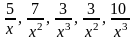 является бесконечно малой и стремится
к нулю.
является бесконечно малой и стремится
к нулю.
Пример 5.
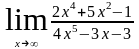
Решение.
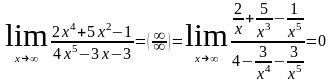 , так как
, так как
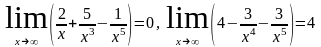 .
.
Для раскрытия неопределенности следует числитель и знаменатель разделить на одну и ту же старшую степень переменной.
Пример 6.

Решение.
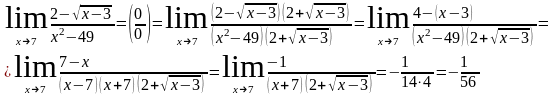
В этом примере нужно было избавиться от радикалов, для чего умножили и числитель и знаменатель на сумму – сопряженное числителю выражение. Применив формулу разности квадратов в числителе, мы избавились от радикалов:
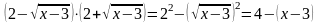 .
.
Задание 21-40 . Найти производные функций.
Пример
1:
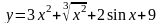
Решение:
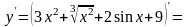
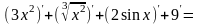

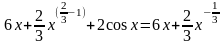 +
+
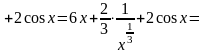
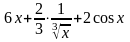 .
.
При
вычислении производной использовали
правило и формулы дифференцирования:
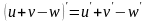 ;
;
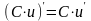 ;
;
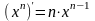 ;
;
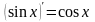 ;
;
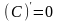 .
.
Пример
2:
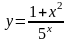
Решение:
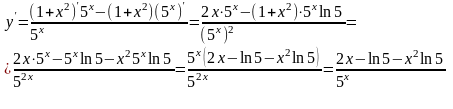
При вычислении производной использовали правила и формулы дифференцирования:
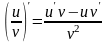 ;
;
;
;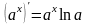 ;
;
.
;
;
.
Пример 3:
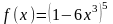
Решение:
вычислим производную сложной степенной
функции, применив формулу дифференцирования
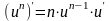 ,
получим
,
получим
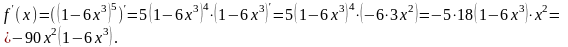
Пример 4:
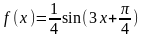
Решение:
вычислим производную сложной
тригонометрической функции, применив
формулу дифференцирования
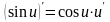 ,
получим
,
получим
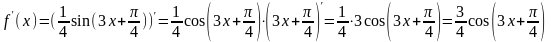
Задание 41-60: Исследовать функцию и построить ее график
Пример: Исследовать функцию и построить ее график:
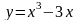 .
.
Решение:
Функция определена на всей числовой оси, т. е. ее область определения
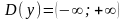 .
.Найдем точки пересечения с осями координат:
с
осью ОХ : решим уравнение
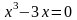
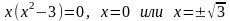 .
.
с
осью ОY:
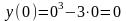
Выясним, не является ли функция четной или нечет
ной:
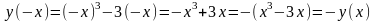 .
.
Отсюда следует, что функция является нечетной.
Функция непериодическая.
Найдем промежутки монотонности и точки экстремума функции:
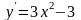 .
.
Критические
точки:
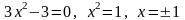 .
.
|
|
-1 |
|
1 |
|
|
+ |
0 |
- |
0 |
+ |
|
|
т. max 2 |
|
т. min -2 |
|
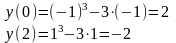
Найдем промежутки выпуклости и точки перегиба функции:

Критические
точки:
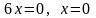 .
.
|
|
0 |
|
|
- |
0 |
+ |
|
|
точка перегиба 0 |
|
Функция непрерывна, асимптот у нее нет.
По результатам исследования построим график функции:
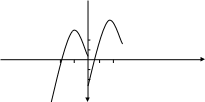
Задание 61-80. Найти неопределенные интегралы и вычислить определенный интеграл:
Пример 1 а) Найти неопределенный интеграл:
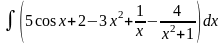 .
.
Решение: =
=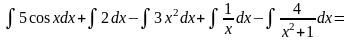
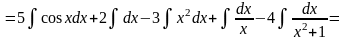
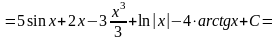
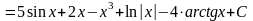 .
.
б)
Найти
неопределенный интеграл:
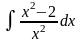 .
.
Решение:
=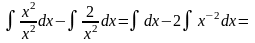
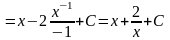 .
.
в)
Найти
неопределенный интеграл
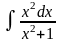
Решение:
=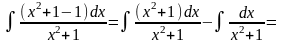
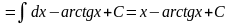
Пример
2. а)Найти
неопределенный интеграл
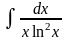
Решение:
=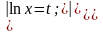
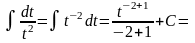
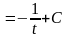
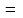
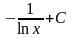
б)
Найти неопределенный интеграл
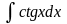
Решение: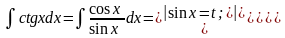
=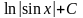
в)
Найти неопределенный интеграл
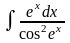
Решение:
=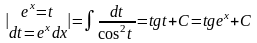
г)
Найти неопределенный интеграл

Решение:
=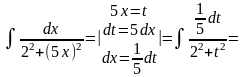
=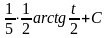 =
=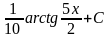 .
.
Пример
3 а) Вычислить определенный интеграл
методом замены переменной

Решение:
=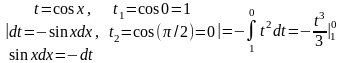
 .
.
б)
Вычислить определенный интеграл:
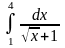 .
.
Решение:
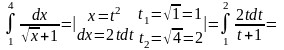
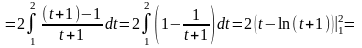
 .
.
Задание 81-100. Сделать чертеж и с помощью определенного интеграла вычислить:
Пример 1. Найти площадь фигуры, ограниченной линиями:
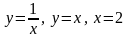 .
.
Решение.
Площадь данной фигуры равна разности
площадей криволинейных трапеций,
образованных прямой
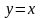 и гиперболой
и гиперболой
 на отрезке
на отрезке
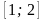 .
.
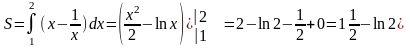 .
.
Пример 2. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
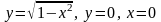 .
.
Решение.
Используем формулу для нахождения
объёма тел вращения:
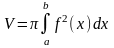 .
.
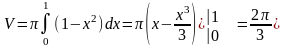 .
.
Таблица производных основных элементарных и сложных функций
х- независимая переменная, u=u(x)-дифференцируемая функция
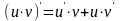
|
1.2.
1.3.
1.4
1.5.
1.6
1.7
1.8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
|
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
2.14
2.15 |
Таблица интегралов
1. 2. 3. 6. 7.
|
4. 5. 8. 9.
|