Var а, в, d, к, X, y : integer;
BEGIN
WRITELN('BBEДИTE ДВА НАТУРАЛЬНЫХ ЧИСЛА');
READLN(A, В);
К := 0;
IF A>B THEN
BEGIN
X:=B;
Y:=A
END
ELSE
BEGIN
Y := B;
X:=A
END;
REPEAT
K:= K+Y DIV X;
D.= Y MOD X;
Y:= X;
X:= D;
UNTIL D = 0;
WRITELN('ИCKOMOE ЧИСЛО КВАДРАТОВ : ', К)
END.
Для решения задачи:
- формируем тело программы и описываем переменные;
- создаем описание функций MIN и МАХ;
- вводим два натуральных числа А и В;
- присваиваем начальные значения вспомогательным переменным;
- организуем цикл, в котором сторона У уменьшается каждый раз до величины X, а само X становится равным Y MOD X;
- цикл работает до тех пор, пока У не станет кратным X;
- завершаем работу программы.
Переменные:
в основной программе;
А, В - два натуральных числа (глобальные переменные);
D, X, Y - вспомогательные переменные;
К - количество отрезаемых квадратов.
З
адача
9.9 Дан
прямоугольный бильярдный стол со
сторонами А и В, где А, В - натуральные
числа (бильярд Льюиса Кэрролла -рис.
9.2). Из угловой лузы вылетает шар под
углом 45 градусов к боковым стенкам,
ударяется о борт, отскакивает, ударяется
еще раз и т. д., пока не вылетит через
одну из угловых луз. Рассчитать количество
отрезков в ломаной траектории шара.
Считать угол падения равным углу
отражения.
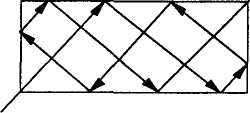
Рис. 9.2. Бильярд Льюиса Кэрролла
Данная задача решается с помощью стандартных функций вы деления целой части от деления Y на X Y DIV X и выделения ос татка Y MOD X.
При прохождении шаром прямоугольного стола и отражении его от боковых сторон происходит увеличение числа отрезков траектории на два, а обратный путь вычисляется как Y := A – X+Y MOD X, где Y - обратный путь для шара, А - длинная сторона стола, X - короткая сторона стола.
PROGRAM PG9_9;
Var а, в : integer;
FUNCTION BILL(Y, X : INTEGER): INTEGER;
Var к: integer;
BEGIN
К:=0;
WHILE Y MOD X <> 0 DO
BEGIN
К := K+Y DIV X+2;
Y := A-X+Y MOD X;
END;
BILL := K+Y DIV X
END;
BEGIN
REPEAT
WRITE('BBEДИTE ДВА НАТУРАЛЬНЫХ ЧИСЛА А>В');
READLN(A, В);
UNTIL A> = B;
WRITELN('КОЛИЧЕCTBO ОТРЕЗКОВ В ТРАЕКТОРИИ :', BILL(A, В))
END.
Для решения задачи:
- формируем тело программы и описываем переменные;
- создаем описание функции BILL;
- вводим два натуральных числа А и В;
- вызываем функцию BILL для определения количества отрежов;
- завершаем работу программы.
Переменные:
в функции BILL:
X, Y - два натуральных числа (формальные параметры);
К - вспомогательная переменная (локальная переменная);
А - длинная сторона стола (глобальная переменная);
в основной программе:
А, В - два натуральных числа (глобальные переменные).
Описание функций и процедур может строиться с помощью рекурсии, т. е. обращения их к самим себе. При каждом новом обращении к подпрограмме значения используемых параметров заносятся в стек, причем параметры предыдущих обращений также сохраняются.
Формально рекурсию для функции F(X) можно описать следующим образом:
IF X = <начальное значение> THEN
F := <начальное значение функции>
ELSE
F := W(F);
где конструкция F := <начальное значение функции> называется глубиной рекурсии, a F := W (F) определяет способ обращения функции в точке Хп к своим значениям для меньших значений аргумента Хп - 1, Хп - 2 и т. д.
Классическим примером простейшей рекурсии (линейной) может служить функция вычисления факториала натурального числа N FACT(N).
IF N = 0 THEN
FACT := 1
ELSE
FACT := N * FACT(N - 1);
Например, при N = 4 к функции FACT происходит обращение 5 раз (для N = 4, N = 3, N = 2, N = 1, N = 0), каждое из которых, кроме последнего, заносится в стек. При 5-м обращении вычисляется FACT(O) = 1, и затем последовательно, извлекая обращения из стека, вычисляются
FACT(1) = 1* FACT(O) = 1,
FACT(2) = 2*FACT(1) = 2,
FACT(3) = 3* FACT(2) = 6,
FACT(4) = 4*FACT(3) = 12.
Рассмотрим несколько примеров построения рекурсии. При использовании рекурсий следует помнить, что размеры стека не бесконечны и переполнение его возникает довольно быстро.
Задача 9.10 Вычислить I-е число Фибоначчи.
Известно, что каждое последующее число Фибоначчи равняется сумме двух предыдущих:
F i := F i-1 + F i-2 ; а нулевое число равно нулю, первое - единице.
Данная задача относится к каскадным рекурсиям, когда для вычисления одного значения требуется несколько вызовов для разных предыдущих значений.
PROGRAM PG9J0;