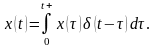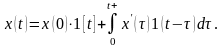- •Основи теорії автоматичного управління
- •Частина 1. Лінійні системи
- •1. Загальна характеристика об'єктів і систем автоматичного керування
- •1.1 Короткі історичні відомості
- •1.2 Основні поняття і визначення
- •1.3 Принципи регулювання
- •1.4 Приклади систем автоматичного регулювання в хімічній технології
- •1.5 Класифікація систем автоматичного керування
- •1.6 Тренувальні завдання
- •1.7 Тести
- •2 Регулярні сигнали і їх характеристики
- •2.1 Визначення регулярного сигналу
- •2.2 Основні типи регулярних сигналів. Періодичні і безперервні сигнали
- •Перетворення Фурье, його основні властивості
- •Спектри сигналів
- •2.5 Розподіл енергії в спектрах сигналів
- •Практична ширина спектру і спотворення сигналів
- •2.7 Представлення сигналів
- •2.8 Сигнали. Їх види
- •2.9 Тренувальні завдання
- •2.10 Тести
- •3.Математичний опис автоматичних систем
- •3.1 Основні способи математичного опису. Рівняння руху.
- •3.2 Приклади рівнянь об'єктів керування
- •3.2.1 Гідравлічний резервуар
- •3.2.2 Електрична ємкість
- •3.2.3 Хімічний реактор повного перемішування
- •3.3 Визначення лінійної стаціонарної системи. Принцип суперпозиції
- •3.4 Динамічне поводження лінійних систем
- •3.5 Динамічні процеси в системах
- •3.6 Перехідна і вагова функції
- •3.6.1 Перехідна функція
- •3.6.2 Вагова функція
- •3.7 Інтеграл Дюамеля
- •Перетворення Лапласа
- •Визначення перетворення Лапласа
- •Властивості перетворення Лапласа
- •Рішення диференціальних рівнянь
- •Розбиття на прості дроби
- •Передаточна функція
- •3.10 Тренувальні завдання
- •3.11 Тести
- •4 Частотний метод дослідження лінійних систем
- •4.1 Елементи теорії функції комплексного змінного
- •4.2 Частотні характеристики
- •4.3 Зв'язок перетворень Лапласа і Фур’є
- •4.4 Зв'язок диференціального рівняння з частотними характеристиками
- •4.5 Фізичний сенс частотних характеристик
- •4.6 Мінімально-фазові системи
- •4.7 Поняття про логарифмічні частотні характеристики
- •4.8 Взаємозв'язок динамічних характеристик
- •4.9 Тренувальні завдання
- •4.10 Тести
- •5 Структурний аналіз лінійних систем
- •5.1 Ланка направленої дії
- •5.2 Типові динамічні ланки
- •5.2.1 Підсилювальна ланка
- •5.2.2 Інтегруюча ланка
- •5.2.6 Ланка чистого запізнювання
- •5.2.7 Аперіодична ланка першого порядку
- •5.2.8Ланка щоінерційно-форсуює
- •5.2.9 Аперіодична ланка другого порядку
- •5.2.10 Коливальна ланка
- •5.2.11 Особливі ланки
- •5.3 Основні способи з'єднання ланок
- •5.3.1 Структурні схеми
- •5.3.2 Паралельне з'єднання ланок
- •5.3.3 Послідовне з'єднання ланок
- •5.3.4 З'єднання із зворотним зв'язком
- •5.3.5 Передаточні функції замкнутої системи
- •5.3.6 Правила перетворення структурних схем
- •5.3.7 Формула мейсона
- •5.4 Типові закони регулювання
- •5.4.1 Пропорційний закон регулювання
- •5.4.2 Інтегральний закон регулювання
- •5.4.3 Диференційний закон регулювання
- •5.4.4 Пропорційно-диференційний закон регулювання
- •5.4.5 Пропорційно-інтегральний закон регулювання
- •5.4.6 Пропорційно-інтегрально-диференційний закон регулювання
- •5.5 Тренувальні завдання
- •5.6 Тести
- •6 Стійкість лінійних систем
- •6.1 Поняття стійкості і її визначення
- •6.2 Стійкість лінійного диференціального рівняння з постійнимикоефіцієнтами
- •6.3 Зображення руху у фазовому просторі
- •6.3.1 Поняття фазового простору
- •6.3.2 Фазові портрети лінійних систем другого порядку
- •6.4 Поняття стійкості руху
- •6.5 Основні види стійкості
- •6.5.1 Орбітальна стійкість
- •6.5.2 Стійкість по ляпунову
- •6.5.3 Асимптотична стійкість
- •6.6 Необхідна умова стійкості
- •6.7 Алгебраїчні критерії стійкості
- •6.7.1 Критерій стійкості рауса
- •6.7.2 Критерій стійкості гурвіця
- •6.7.3 Критерій стійкості л’єнара-шипаро
- •6.7.4 Стійкість і стала похибка
- •6.7.5 Область стійкості
- •6.8 Частотні критерії стійкості
- •6.8.1 Принцип аргументу
- •6.8.2 Критерій міхайлова
- •6.8.3 Критерій найквіста
- •6.8.4 Застосування критеріїв для дослідження стійкості систем
- •6.8.5 Аналіз стійкості по логарифмічних частотних характеристиках
- •6.9Тренувальні завдання
- •6.10 Тести
- •7. Синтез стійких систем з необхідним запасом стійкості
- •7.1 Стійкість ланок і систем. Запас стійкості.
- •7.2 Межі стійкості систем
- •7.2.1 Межа стійкості для систем з пі-регулятором
- •7.2.2 Межа стійкості для систем з пі-регулятором
- •7.2.3 Межі стійкості для системи з і-регулятором
- •7.3 Запас стійкості і його оцінка
- •7.3.1 Кореневі методи оцінки запасу стійкості
- •7.3.2 Частотні методи оцінки запасу стійкості
- •7.4 Розширені частотні характеристики
- •7.5 Аналіз систем на запас стійкості
- •7.6 Синтез систем з необхідним запасом стійкості
- •Система с п-регулятором
- •7.6.2 Система с і-регулятором
- •7.6.3 Система с пі-регулятором
- •7.6.4 Система з пд-регулятором
- •7.7 Використання логарифмічних частотних характеристик для забезпечення стійкості і заданого запасу стійкості
- •7.8 Структурно-стійкі системи
- •7.9 Малі параметри систем і їх вплив на стійкість
- •7.10 Використання корегуючих пристроїв для забезпечення стійкості і запасу стійкості
- •7.10.1 Послідовна корекція
- •7.10.2 Паралельна корекція
- •7.11 Тренувальні завдання
- •7.12 Тести
- •8.Якість процесів регулювання і методи її аналіза
- •8.1 Показники якості регулювання
- •8.1.1 Прямі показники якості регулювання
- •8.1.2 Непрямі показники якості регулювання
- •8.1.3 Інтегральні критерії якості регулювання
- •8.1.3.1 Лінійний інтегральний критерій
- •8.1.3.2 Модульний інтегральний критерій
- •Інтегральний квадратичний критерій
- •8.2 Частотні методи аналізу якості регулювання
- •8.2.1 Залежність між перехідною і частотними характеристиками
- •8.2.2 Властивості дійсно-частотних характеристик і відповідних їмперехідних процесів
- •8.3 Поняття про чутливість систем автоматичного регулювання
- •Тренувальні завдання
- •8.5 Тести
- •9 Методи розрахунку настроювальних параметрів для сар
- •9.1 Постановка задачі
- •9.2 Вибір оптимальних настройок регуляторів методом незгасаючих коливань
- •9.3 Алгоритм розрахунку області настройок типових регуляторів
- •9.4 Графоаналітичний метод розрахунку
- •9.5 Тренувальні завдання
- •9.6 Тести
- •Частина 2 нелінійні системи
- •10 Методи лінеаризації характеристик нелінійних систем
- •10.1 Особливості нелінійних систем
- •10.2 Типові нелінійні елементи систем керування
- •10.3 Методи лінеаризації
- •10.3.1 Розкладання в ряд Тейлора
- •10.3.2 Гармонійна лінеаризація
- •10.3.3 Вібраційна лінеаризація
- •10.4 Тренувальні завдання
- •10.5 Тести
- •11 Дослідження нелінійних систем методом фазового простору
- •11.1 Загальні відомості про метод фазового простору
- •Фазові портрети нелінійних систем другого порядку
- •Методи побудови фазових портретів
- •11.3.1 Інтегрування рівнянь фазових траєкторій
- •11.3.2 Метод ізоклін
- •11.3.3 Метод припасовування
- •11.3.4 Метод зшивання
- •11.4 Тренувальні завдання
- •11.5 Тести
- •12 Аналіз нелінійних систем на стійкість і якість
- •Основні види стійкості нелінійних систем
- •Методи дослідження стійкості нелінійних систем
- •12.2.1 Перший метод Ляпунова
- •12.2.2 Другий метод Ляпунова
- •12.2.2.1 Поняття про знаковизначенні, знакопостійні і знакозмінні функції
- •12.2.2.2 ФункціяЛяпунова
- •12.2.2.3 Теореми Ляпунова
- •12.3 Методи побудови функції Ляпунова
- •12.3.1 Функція Ляпунова у вигляді квадратичних форм
- •12.3.2 Побудова функції Ляпунова методом г. Сеге
- •12.3.3 Побудова функції Ляпунова методом д. Шульца
- •12.3.4 Побудова функції Ляпунова методом Лур’є – Постникова
- •12.4 Приклади побудови функцій Ляпунова
- •12.5 Абсолютна стійкость по критерію Попова
- •12.6 Методи визначення якості регулювання нелінійних систем
- •12.7 Тренувальні завдання
- •12.8 Тести
- •13 Автоколивання в нелінійних системах
- •13.1 Режим автоколивань в нелінійних системах
- •13.2 Методи дослідження автоколивань в нелінійних системах
- •13.2.1 Критерій Бендіксона
- •13.2.2 Метод гармонійного балансу
- •13.3 Тренувальні завдання
- •13.4 Тести
- •14.1. Опис систем у просторі станів
- •14.2. Структура рішення рівнянь змінні стану
- •14.3. Характеристики систем у просторі станів
- •14.4. Нормальна форма рівнянь у просторі станів
- •14.5. Керування по стану. Системи керування
- •14.6. Оцінювання координат стану систем
- •14.7. Прямий кореневий метод синтезу систем керування
- •14.8 Тренувальні завдання
- •14.9 Тести
- •15. Дискретні системи автоматичного керування
- •15.1. Загальні відомості
- •15.2. Структура й класифікація імпульсних систем
- •15.3. Математичний апарат дослідження дискретних систем
- •15.4. Передатні функції розімкнутих імпульсних систем
- •15.5 Структурні схеми і передатні функції
- •15.6. Частотні характеристики імпульсних систем
- •15.7 Стійкість імпульсних систем
- •15.8. Перехідні процеси в імпульсних системах
- •Перехідний процес
- •15.9 Точність і корекція імпульсних систем
- •15.10. Опис дискретних систем у просторі станів
- •15.11 Тренувальні завдання
- •15.12 Тести
- •16 Оптимальне керування динамічними системами
- •16.1. Основні поняття систем оптимального керування
- •16.2. Завдання синтезу оптимальних систем
- •16.3. Самонастроювальні і динамічні системи, що самонавчаються, оптимального керування
- •16.4 Тести
- •Загальна характеристика об'єктів і систем автоматичного керування.
- •1.1 Короткі історичні відомості 3
- •Регулярні сигнали і їхні характеристики
- •Математичний опис автоматичних систем.
- •Частотний метод дослідження лінійних систем
- •Структурний аналіз лінійних систем
- •6. Стійкість лінійних систем
- •7. Синтез стійких систем з необхідним запасом стійкості
- •8. Якість процесів регулювання і методи її аналізу
- •9. Методи розрахунку настроювальних параметрів для сар
- •10.Методи лінеаризації характеристик нелінійних систем
- •11.Дослідження нелінійних систем методом фазового простору
- •14. Аналіз і синтез сау у просторі станів
- •15. Дискретні системи автоматичного керування
- •16. Оптимальне керування динамічними системами
2.8 Сигнали. Їх види
Найчастіше в теорії автоматичного управління використовуються наступні сигнали.
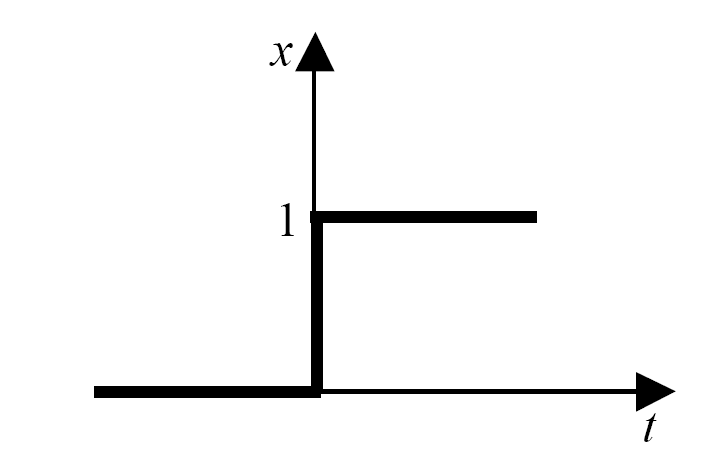
1 Одиничний стрибок (рис. 2.2). 1(t) називається також функцією Хевісайда.
|
(2.16) |
Строго
кажучи, функція Хевісайда фізично не
реалізовується, проте, якщо, наприклад,
на досліджуваному об'єкті різко відкрити
вентиль, внаслідок чого витрата речовини,
що подається, зміниться стрибком з
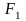 до
до
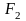 то говорять, що на вході об'єкту
реалізований стрибкоподібний сигнал
величиною
то говорять, що на вході об'єкту
реалізований стрибкоподібний сигнал
величиною
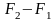 і
якщо остання різниця рівна одиниці, то
на вході реалізується одиничний стрибок.
і
якщо остання різниця рівна одиниці, то
на вході реалізується одиничний стрибок.
Спектральна характеристика для одиничного стрибка:
|
(2.16) |
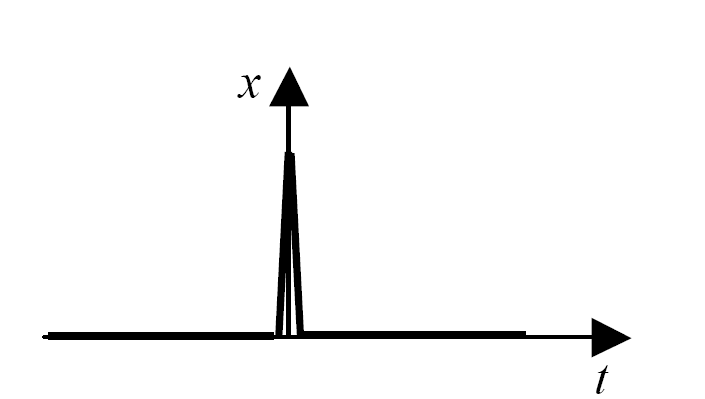
2 Одинична імпульсна функція – дельта-функція (мал. 2.3) – це функція, що задовольняє наступним умовам:
|
(2.17) |
|
|
Рис. 2.2Одиничний стрибок |
Рис. 2.3Одиничний імпульс |
Дельта-функцію
називають також функцією Дираку, вона
відноситься до класу сингулярних
функцій. Цю функцію, що також фізичноне
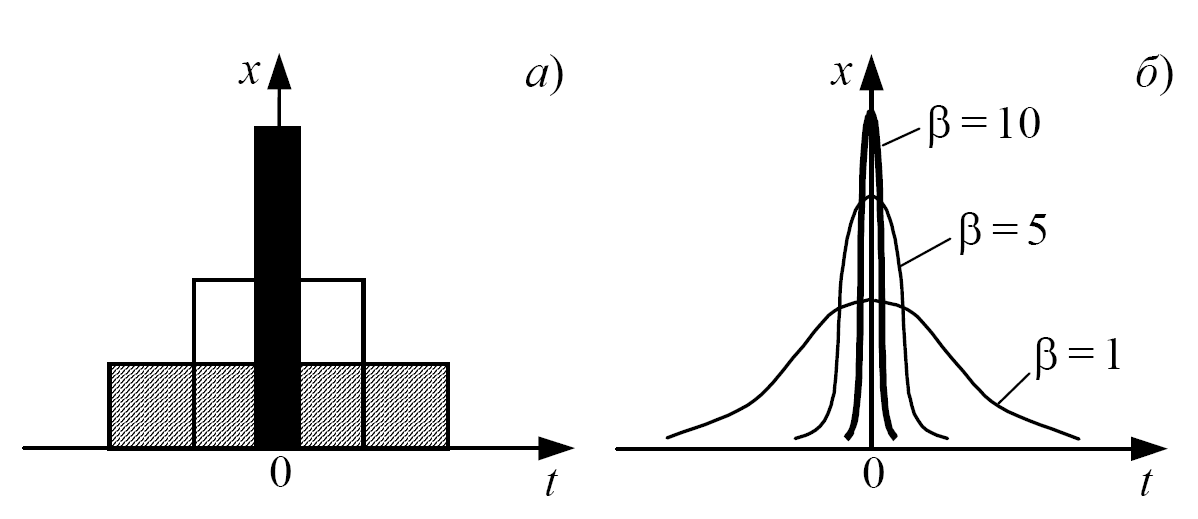
реалізовується, можна представити як
імпульс нескінченно малої тривалості
і нескінченно великої амплітуди, тобто
як межа, до якої наближується прямокутний
імпульс з підставою
 і
площею, рівній одиниці (рис. 2.4, а),
якщо
і
площею, рівній одиниці (рис. 2.4, а),
якщо
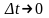 так, щоб площа імпульсу зберігалася
рівній одиниці. Також δ-функцию
можна представити як межу деякої функції
(рис. 2.4, б):
так, щоб площа імпульсу зберігалася
рівній одиниці. Також δ-функцию
можна представити як межу деякої функції
(рис. 2.4, б):
|
(2.18) |
|
Рис. 2.4Представлення дельта-функції: а – прямокутний імпульс; б – δ(у, t) -функція |
До основних властивостей дельта-функції можна віднести наступну рівність:
|
(2.19) |
δ-функція є парною функцією:
|
(2.20) |
|
(2.21) |
тобто з безперервної функції можна "вирізувати" одну ординату.
Останнє співвідношення, використовуючи розглянуті вже властивості δ-функції, доводиться таким чином:
|
|
Спектральна
характеристика дельта-функції:
 .
.
Між функцією Хевісайда і функцією Дираку існує зв'язок, що виражається співвідношенням
|
(2.22) |
На практиці вважається, що на вхід об'єкту подана δ-функция, якщо час дії прямокутного імпульсу набагато менше часу перехідного процесу.
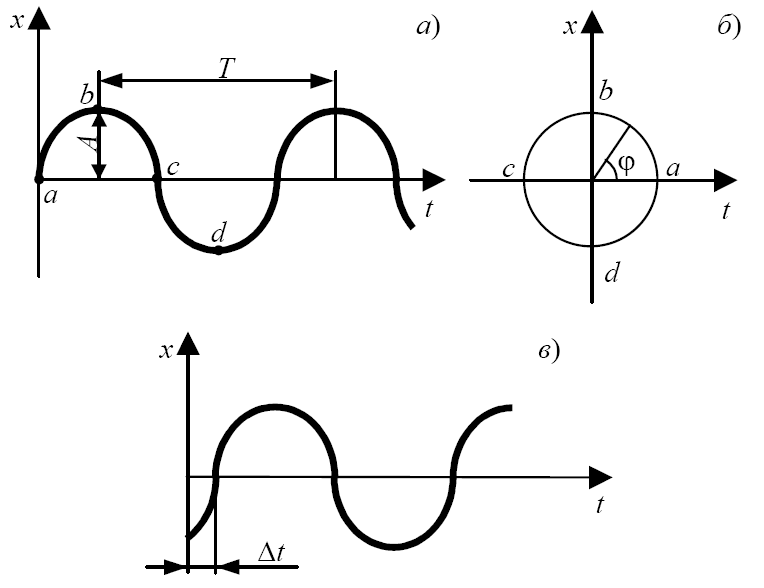
3 Гармонійний сигнал (рис. 2.5, а)
|
(2.23) |
використовується при дослідженні систем автоматичного регулювання частотними методами.
Синусоїдальний гармонійний сигнал можна представити як обертання вектора довжиною навколо початку координат (рис. 2.5, б) з деякою кутовою швидкістю рад/с.
Гармонійний
сигнал характеризується такими
параметрами, як амплітуда –
;
період –
;
фаза –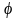 .
.
|
Рис. 2.5Гармонійний сигнал: а – звичайний сигнал; б – представлення гармонійного сигналу обертанням вектора; у – гармонійний сигнал із зрушенням фази |
Між періодом і кутовою швидкістю справедливі співвідношення
|
(2.24) |
Якщо коливання починаються не з нуля, то вони характеризуються фазою коливань (рис. 2.5, в), яка в часовій області характеризується відрізком але зазвичай фазу виражають в радіанах – (рис. 2.5, б). Переклад здійснюється по формулі
|
(2.25) |
На практиці для отримання гармонійного сигналу використовується генератор синусоїдальних коливань.
4 Зсунуті елементарні функції.
До
цих функцій відносяться функції Хевісайда
і Дираку із запізнюванням, тобто
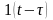 і
і
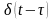 (рис.
2.6),
(рис.
2.6),
|
Рис. 2.6Зсунені елементарні функції |
причому
 .
.
Всі властивості δ-функціїзберігаються, але записуються у вигляді:
|
|
|
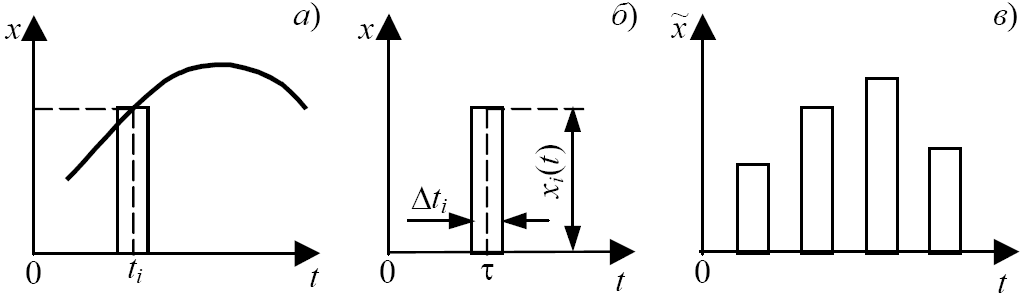
5 Сигнал довільної форми – (рис. 2.10, а).
Будь-який
сигнал довільноїформиможнапредставити
за допомогоюδ-функції.
З цією метою виділяється довільний
момент часу
і
будується стовпчик заввишки
(рис. 2.7, б)відповідний
значенню сигналу у момент часу
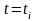 і
основою
і
основою
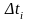 .
.
Цей
імпульс можна виразити через наближену
дельта-функцію –
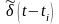
|
|
тобто
 .
.
|
Рис. 2.7Сигнал довільної форми: а – вхідний безперервний сигнал; б – імпульс; в – суперпозиція імпульсів, що визначають сигнал. |
Замінюючи
функцію x(t)
набором
імпульсів (мал. 2.7, в),
можна записати: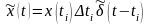 .
.
Якщо
тепер
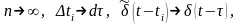 то
то
|
(2.26) |
Сигнал
довільної форми можна представити і
через одиничні функції, для чого вираз
(2.26) слід проінтегрувати по частинах,
використовуючи співвідношення
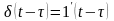 внаслідок чого отримують наступне
співвідношення
внаслідок чого отримують наступне
співвідношення
|
(2.27) |

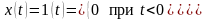 ,
,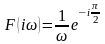 .
. ,
,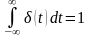
 .
.
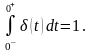
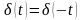 ,
,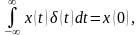
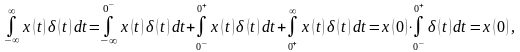
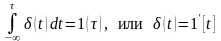
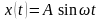

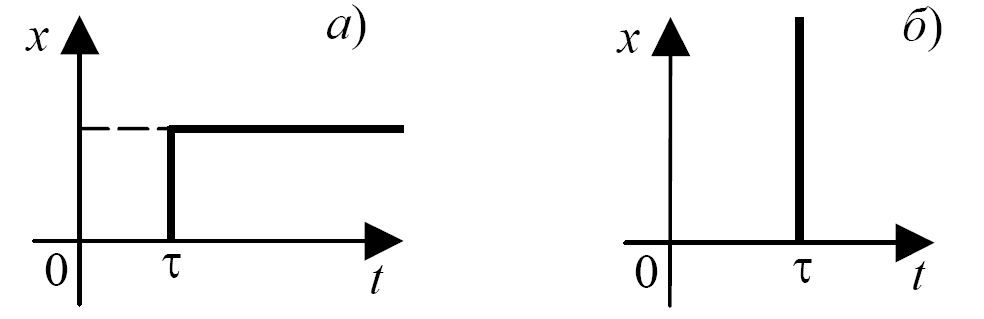
 ;
;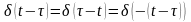 ;
;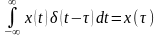 .
.