2.1.2. Сложение положительных чисел

Рассмотрим принцип сложения двух одноразрядных чисел. Результат выполнения этой операции приведен на рис. 2.2. Обратите внимание, что для записи результата сложения двух единиц необходим 2-битовый вектор 10, представляющий значение 2. В этом случае говорят, что сумма равняется 0, а перенос — 1. Для сложения многоразрядных чисел используется метод, аналогичный тому, с помощью которого мы складываем десятичные числа на бумаге. Складываются пары разрядов, начиная с младшего разряда, то есть с правого края битового вектора, с переносом в направлении старшего разряда, то есть левого края битового вектора.

0 1 0 1

+ 0 + 0 + 1 + 1

0 1 1 1 1

Перенос

Рис. 2.2. Сложение одноразрядных чисел

2.1.3. Сложение и вычитание чисел со знаком

Итак, вы уже знакомы с тремя системами представления положительных и отрицательных чисел, или, проще говоря, чисел со знаком. Эти системы различаются только способами представления отрицательных значений. Их сравнительные преимущества с точки зрения выполнения арифметических операций можно определить так: простейшая с точки зрения представления чисел система значения со знаком наименее удобна для их сложения и вычитания. Система дополнения до единицы несколько лучше. А наиболее эффективной с точки зрения выполнения указанных операций является система дополнения до двух.

Чтобы понять принципы арифметики дополнений до двух, нужно рассмотреть операцию сложения по модулю N(обозначаемую как mod N). Удобным графическим представлением сложения положительных чисел по модулю N является круг с N значениями по его периметру: от 0 до N- 1 (рис. 2.3, а). Для примера рассмотрим значение N= 16. Результатом операции (7 + 4) mod 16 является значение 11. Для того чтобы выполнить эту операцию с помощью графического представле­ния, найдите на окружности отметку 7 и переместитесь от нее на четыре деления по часовой стрелке. Там вы найдете ответ — значение 11. Аналогичным образом (9 + 14) mod 16 = 7. Найдя значение 9 и, отсчитав от него 14 делений, вы опишете полный круг и остановитесь на делении 7. Этот нехитрый графический прием по­зволяет вычислить любую сумму (а + b) mod 16 для любых положительных чисел а и b: вы находите число а и перемещаетесь на b делений по часовой стрелке.

Теперь рассмотрим другую интерпретацию окружности mod 16. Предположим, что значения из диапазона от 0 до 15 представлены в соответствии с двоичной системой счисления 4-битовыми двоичными векторами: 0000, 0001,..., 1111. А двоичные векторы, как видно на рис. 2.3, б, представляют числа со знаком от -8 до +7, что соответствует системе дополнения до двух (рис. 2.1).

Давайте применим графическую технологию сложения по модулю 16 к простому примеру сложения чисел +7 и -3. В системе дополнения до двух эти числа представлены как 0111 и 1101 соответственно. Для того чтобы их сложить, найди­те на окружности число 0111 и переместитесь на 1101 шагов по часовой стрелке (то есть на 13 шагов — сосчитайте количество делений от 0 до 1101). Вы окажетесь на делении 0100, представляющем ответ, а именно +4 (рис. 2.3, б). Если вы выполните эту операцию путем сложения пар разрядов справа налево, результат будет таким:

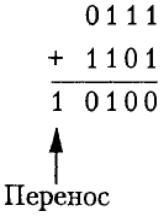
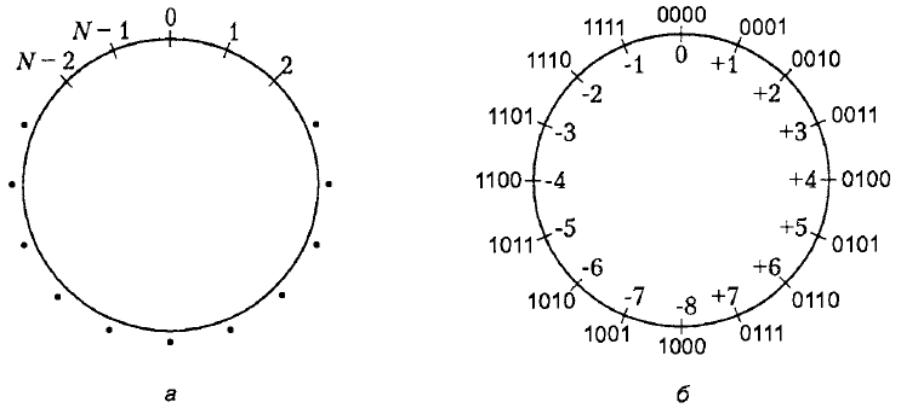
Как видите, для получения правильного результата мы проигнорировали пе­ренос из четвертого разряда. В этом и состоит суть сложения по модулю. Перемещаясь по кругу (рис. 2.3, б), мы возвращаемся не к значению 10000, следующему за значением 1111, а к значению 0000.

Рис. 2.3. Сложение по модулю и сложение в системе дополнения до двух:

представление операций над целыми числами по модулю N (а); операции

над числами в формате дополнения до двух по модулю 16 (б)

Теперь мы можем описать правила сложения и вычитания n-разрядных чисел со знаком в системе дополнения до двух.

Для сложения двух чисел следует сложить их n-разрядные представления, игнорируя сигнал переноса из позиции старшего разряда (MSB). Суммой будет алгебраически правильное значение, представленное в системе дополнения до двух, если это значение лежит в диапазоне от -2^n-1 до +2^n-1 - 1.

Для вычитания чисел X и Y, то есть выполнения операции X — Y, следует вычислить дополнение числа Y до двух, а затем добавить его к числу Y с учетом правила 1. Результатом будет алгебраически правильное значение, представленное в системе дополнения до двух, если это значение лежит в диапазоне от -2^n-1 до +2^n-1 -1.

На рис. 2.4 показано несколько примеров сложения и вычитания 4-разрядных двоичных чисел. Во всех этих примерах ответ оказывается в диапазоне от -8 до 7. Если ответ выходит за границу указанного диапазона, мы говорим, что произошло арифметическое переполнение. Такие ситуации рассматриваются в следующем разделе. Представленные здесь четыре операции сложения (рис. 2.4, а-г) выполнены по правилу 1, а шесть операций вычитания (рис. 2.4, д-к) — по правилу 2. В операции вычитания для вычитаемого (нижнее значение) сначала выполняется вычисление дополнения, а затем сложение — точно так же, как в случае двух по­ложительных чисел.

В программировании часто возникает необходимость выразить некоторое число, заданное в системе дополнения до двух, с использованием определенного количества разрядов, большего, чем необходимо для представления этого числа на самом деле. Если речь идет о положительных числах, для этого достаточно просто добавить слева нужное количество нулей. В случае отрицательных чисел крайний слева бит, представляющий знак числа, должен быть равен 1, и для получения более длинного представления того же значения нужно повторить знаковый бит слева от числа столько раз, сколько нужно для достижения заданной длины. Чтобы понять, почему нужно действовать именно так, давайте снова вернемся к окружности для сложения по модулю 16, показанной на рис. 2.3, б. Сравните эту окружность с окружностью для сложения по модулям 32 и 64. Представление отрицательных чисел, -1, -2 и т. д., будет точно таким же, с дополнительной единицей слева. Операция добавления единицы называется расширением знака.

а 0010 (+2) б 0100 (+4)

+ 0011 (+3) + 1010 (-6)

0101 (+5) 1110 (-2)

в 1011 (-5) г 0111 (+7)

+ 1110 (-2) + 1101 (-3)

1001 (-7) 0100 (+4)

д 1101 (-3) 1101

- 1001 (-7) - 0111

0100 (+4)

е 0010 (+2) 0010

- 0100 (+4) + 1100

1110 (-2)

ж 0110 (+6) 0110

- 0011 (+3) + 1101

0011 (+3)

з 1001 (-7) 1001

- 1011 (-5) + 0101

1110 (-2)

и 1001 (-7) 1001

- 0001 (+1) + 1111

1000 (-8)

к 0010 (+2) 0010

- 1101 (-3) + 0011

0101 (+5)

Рис. 2.4. Операции сложения и вычитания в системе дополнения до двух

Теперь вы знаете, насколько просто выполняется сложение и вычитание чисел со знаком в системе дополнения до двух. Поэтому для представления чисел в со­временных компьютерах выбрана именно эта система. Может показаться, что и система дополнения до 1 не хуже, но это только на первый взгляд. Хотя вычислить дополнение до единицы и проще, результаты операции сложения не всегда оказываются правильными. В данном случае нельзя игнорировать перенос, с_n.

Если с_n = 0, полученный результат будет верным. Но если с_n= 1, то для определе­ния точного результата к полученному значению нужно добавить 1. Необходимость в этом поправочном цикле, зависящая от значения переноса, делает опера­ции сложения и вычитания в системе дополнения до единицы более сложными, чем в системе дополнения до двух.