15.Нармальная плоскасць прасторавай крывой.

Нармальную пл-цю прасторавай крывой γ ў яе пункце Р наз пл-ць β. Якая праходзіць праз пункт Р крывой γ перпендыкулярна датычнай прамой Т крывой γ.

Сцв1. Усякая гладкая прасторавая крывая γ ў кожным сваім пункце Р мае нармальную пл-ць β і пры тым толькі адну

Заўвага: Калі пункт Р крывой γ мае каардынаты(), а вектар ў пункце Р мае каардынаты (), тады раўнанне нармальнай пл-ці β ў пункце Р можна запісаць ў выглядзе:

Сцв2. Калі гладкая прасторавая крывая γ зададзена няяўна сіс-май:

І вектар існуе непарыўны і адрозніваецца ад нуль вектара ўздоўж γ, тады в-р ёсць нармальны в-р нармальнай пл-ці β крывой γ у яе пункце Р(х,у,z)

16*.Вугал паміж крывымі.

Вуглом паміж крывым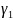і і 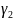у пункце Р перасячэння Р будзем лічыць адвольный з двух смежных вуглоў 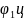і 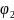паміж іх датычнымі прамымі 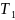і праведзенымі ў пункце Р.

Сцв.1 Калі 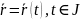дапушчальная параметрызацыя гладкай крывой , а 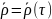, 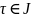. Тады вугал 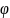паміж крывымі і у іх пункце перасячэння 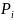можна знайсці з дапамогай ф-лы:

Cos = , дзе Р(

17.Даўжыня дугі крывой

Даўжынёй дугі 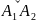гладкай крывой наз. Лік ( )= (1), дзе v=v(t)-вектар хуткасці адвольнай дапушчальнай параметрызацыі r=r(t) t крывой γ.

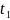і 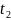-параметры пунктаў адносна параметрызацыі

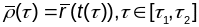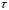Заўвага: Азначэнне карэктна ў тым сэнсе, што не залежыць ад выбару дапушчальнага параметра. На самой справе , гэта значыць . Дыфферэнцыруя па будзем мець , , , , .

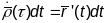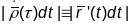18.Формулы для вылічэння даўжыні дугі.

Спецыяльныя формулы для вылічэння даўжыні дугі:

1.Калі прасторавая крывая 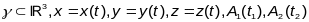, t (параметрычнае раўнанне)

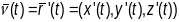
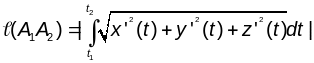
2.Калі γ-гладкая простая крывая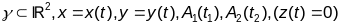

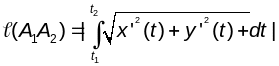
(3)Калі γ графік гладкай ф-цыі y=y(x),х . Тады γ можна параметрызаваць γ:x=t, y=y(t), t

r(t)=(t,y(t)), t

|v(t)|=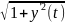

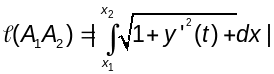
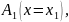
Калі γ плоская гладкая крывая зададзеная палярнымі каардынатамі: ρ=ρ(φ) ,φ∈І

,

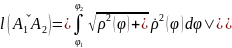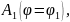
19**.Натуральная параметрызацыя крывой

20**.Судатыкальная плоскасць

21.Суправаджальны трохграннік прасторавай крывой.

Няхай - бірэгулярная прасторавая крывая ,

r=r(t), t∈J-нейкая дапушчальная параметрызацыя. Р(t)∈(γ,r), Т – датычная прамая да γ ў пункце Р(t), - нармальная пл-сць ў пункт Р, а π-сутыкальная пл-сць.

праз пункт Р(t) праходзіць бясконцае мноства нармаляў да крывой 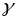, якія ляжаць у нармальнай пл-ці 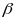да крывой γ у пункце Р, тая з іх якая да тако ж ляжыць ў сутыкальнай пл-ці π наз. Галоўнай нармаллю(N), а тая якая перпендыкулярна пл-ці π наз. Бінармальная(β).

Плоскасць, якая праходзіць праз датычную прамую Т і бінармаль β наз. Выпрастоўнай і абазн. Праз α

Суправаджальным трохграннікам прасторовай крывой 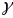у яе пункце Р называецца трохгранны вугал з вяршынай ў пункце Р крывой γ, кантамі якога з’яўл. Т,N,β, а гранямі π,β,α

Сцв.У кожным пункце Р бірэгулярнай крывой γ існуе суправаджальны трохграннік і пры тым толькі адзін, відавочна