2. Элементарные крывыя

Гамеаморфным(тапалагічным) пераутварэннем фігуры А на фігуру В наз. Узаемна-адназначная і узаемна непарыўная адл-нне фігуры А на В.

Будзем наз. Элементарным прамежкам прамой, з наступных яе падмн-ваў: адрэзак, адрэзак без 1-го ці 2-ых канцоў, прамень(з пачатку або без), усю прамую, саму прамую

Азн1. Элементарнай крывой(э.к) у пр-ры( на пл-ці) наз. Гамеаморфны вобраз элементарнага прамежка прамой ў гэтую прастору(на плоскасць).

Будзем абазначаць э.к. праз

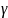
Тыпы э.к:

1)адрэзак; 2) адрэзак без аднаго канца; 3) адрэзак без 2-х канцоў; 4)дуга; 5)прамень з пачаткам; 6) прамень без пачатку; 7)уся прамая;

Такім чынам э.к-усякія дугі з адным ці двумя канцамі, ці бясконцыя ў адзін бок, ці ў два бакі;

Прыклады:

1)элементарныя прамежкі самі з’яўляюцца э.к.

2)дугі акружнасці(замкнутая, адкрытая, паўадкрытая, паўзамкнутая, з 2-мя канцамі, з 1-ым канцом)

3)сінусоіда, касінусоіда;

3.Агульныя крывыя

Азн.1Агульнай крывой(а.к.) наз. Фігура ў пр-ры(на пл-ці), якую можна пакрыць канечнай ці злічонай колькасць э.к.

Абазначаецца .

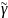Азн2.Пакрыццём мн-ва Х наз. Адвольная сукупнасць яго падмн-ваў 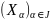, такая што X=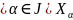

Сцв1: калі пункт P а.к. , належыць некаторай э.к.тады 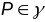, якая змяшчаецца ў крывой .

Вынік: вывученне агульных крывых у малым( у класічнай ДГ) зводзіцца да вывучэння э.к.

Прыклады а.к.:

1)усякая э.к. ёсць а.к;

2)тангенсоіда; 3)акружнасць; 4) гіпербала; 5)прамень;

Тапалагічна звычайны пункт а.к. – такі яе пункт, які мае адкрытае наваколле ў пр-ры(на пл-ці), перасячэнне якога з гэтай крывой ёсць э.к.

Адкрытым наваколлем пункта на пл-ці( у пр-ры) будзем наз. Унутраннасць адвольнага круга(шара) з цэнтрам у гэтым пункце.

Заўвага: Усе пункты крывых раней прыведзяных прыкладаў-тапалагічна звычайныя, але усё ж тапалагічна-звычайным а.к. наз. Яе унутраным пунктам, калі існуе яго адкрытае наваколле, перасячэнне якога з ёсць э.к. без двух канцоў.

Тапалагічна-звычайны пункт а.к., які не з’яўл. Ўнутранным наз. Яе канцавым пунктам, часам краявым ці канцом.

Пункты а.к., якія не тапалагічна-звычайныя наз. Тапалагічна асаблівымі

5.Параметрычны спосаб задання элементарных крывых

Э.к. ёсць вобраз ў пр-ры(на пл-ці) элементарнага прамежка J пры тапалагічным(гамеаморфным) адл-ння

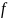
Адл-нне наз. Параметрызацыяй э.к.

Увядзём на прамой і ў пр-ры(на пл-ці), якія-небудзь каардынаты, напрыклад дэкартавы.

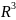Тады прамая пераўтвараецца ў лікавую прамую , а пр-ра ў пунктава-вектарную пр-ру . Тады кожны пункт t, які належыць J пераўтвараецца ў некатары пункт P(t)=f(t) Э.к.

Няхай –радыўс вектар пункта P(t), ён мае каардынаты .

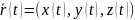Калі t прабягае прамежак J ўзнікае вектар-функцыя

.

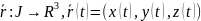параметрызацыі f адносна ўведзяных на прамой і ў пр-ры каардынат, а таксама простай параметрызацыяй э.к. γ

Кароткі запіс параметрызацыі :

Роўнасць (1) наз.таксама вектарным параметрычным раўнаннем э.к.γ

Наз. Яе скалярным параметрычным раўнаннем

Параметр t наз. Параметрам ці ўнутранай каардынатай адпаведнага пункта P(t) э.к.γ адносна ўведзяных каардынат.

Часам пішуць:

Сцв. Кожная э.к.γ дапускае бясконцую кол-сць розных параметрызацый і адпаведна параметрычных раўнанняў.

Калі зафіксаваць нейкую параметрызацыю э.к.γ атрымаем элементарную параметрызаваную крывую, г.з. пару (), пры гэтым γ наз. Нозбітам параметрызацыі

Заўвага: Ў пр-ры(на пл-ці) можна ўводзіць не толькі дэкартавы каардынаты, але і адвольныя іншыя, напрыклад, палярныя(на пл-ці), сферычныя ці цыліндрычныя(ў пр-ры)