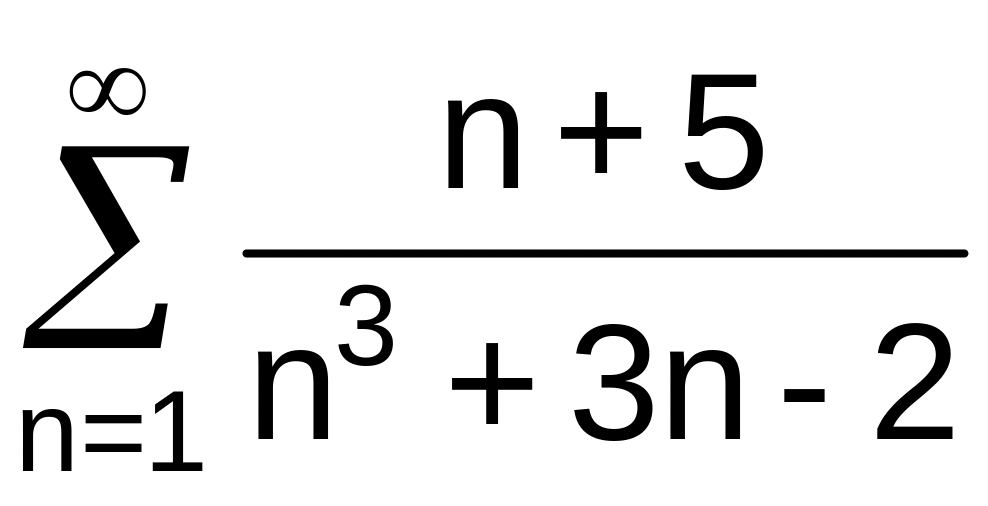Решение.

Исходное уравнение является неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами и правой частью, вида: , где ,  многочлен степени .

Общее решение дифференциального уравнения имеет вид: , где  общее решение однородного дифференциального уравнения , а  частное решение неоднородного дифференциального уравнения.

Решим характеристическое уравнение , производя в уравнении замену , и .

Тогда

.

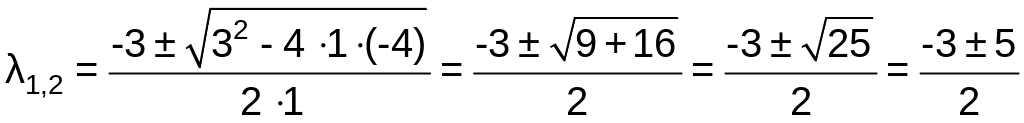Откуда и .

Если характеристическое уравнение имеет два различных действительных корня и , то общее решение соответствующего однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Следовательно,  общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами .

Найдем частное решение исходного дифференциального уравнения, которое будем отыскивать в виде: , так как не является корнем характеристического уравнения. Так как и , то, подставляя , , в исходное уравнение, получим:

или

.

Откуда

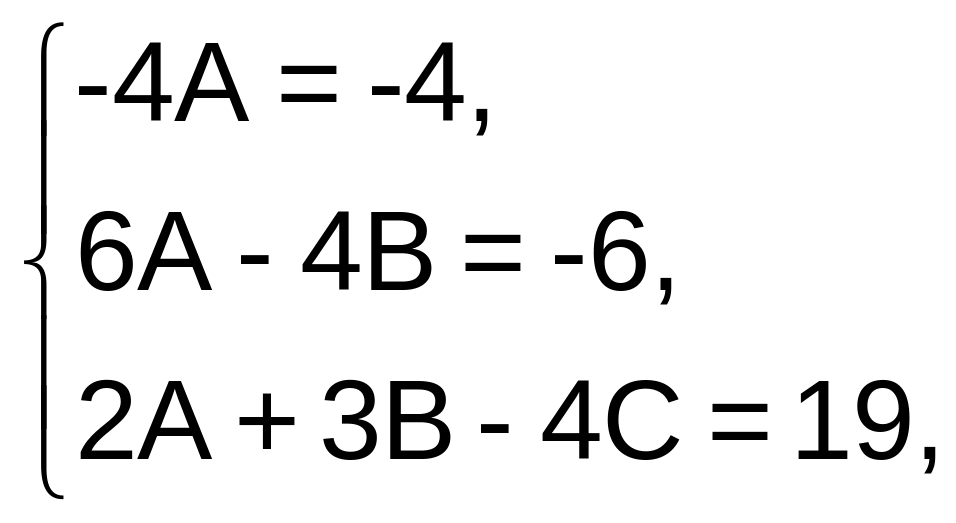и

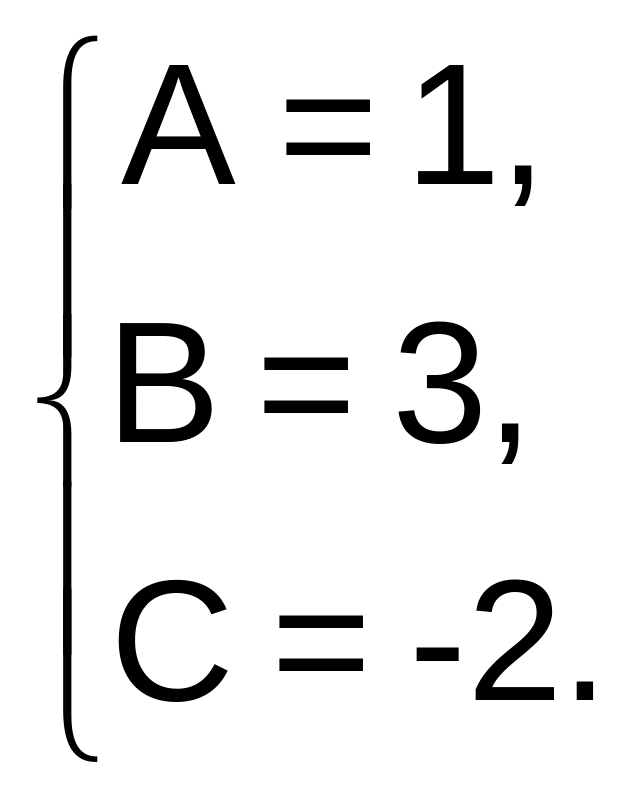
Следовательно,

 частное решение исходного дифференциального уравнения.

Таким образом,

 общее решение дифференциального уравнения.

Ответ: .

№10. Найти общее решение дифференциального уравнения:

.

Решение.

Исходное уравнение является неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами и правой частью вида: , где ,  многочлен степени .

Общее решение дифференциального уравнения имеет вид: , где  общее решение однородного дифференциального уравнения , а  общее решение неоднородного дифференциального уравнения.

Решим характеристическое уравнение , производя в уравнении замену , и .

Тогда

.

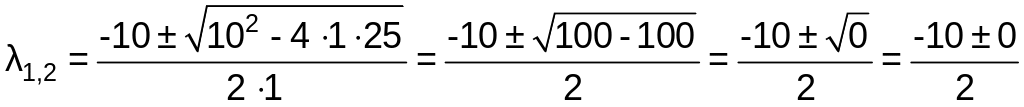Откуда .

Если характеристическое уравнение имеет два равных действительных корня (кратный корень), то общее решение соответствующего однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Следовательно,  общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами .

Заметим, что если характеристическое уравнение имеет два различных действительных корня и , то общее решение соответствующего однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Найдем частное решение исходного дифференциального уравнения, которое будем искать в виде: , так как является кратным корнем характеристического уравнения.

Заметим, что если является одним из действительных корней характеристического уравнения, то частное решение исходного дифференциального уравнения имеет вид:

.

Так как

и

,

то, подставляя , , в исходное уравнение , получим:

или

, т. е. .

Откуда , т. е. .

Следовательно,

 частное решение исходного дифференциального уравнения.

Таким образом,

 общее решение дифференциального уравнения.

Ответ: .

№11. Исследовать сходимость ряда: а)