
Задание 1
Задана
функция ![]() .
Требуется:
.
Требуется:
а) найти частные производные второго порядка функции z;
б)
найти градиент функции z
в точке ![]() ;
;
в)
вычислить производную функции z
в точке ![]() в направлении вектора
в направлении вектора ![]() ;
;
г) исследовать на экстремум.
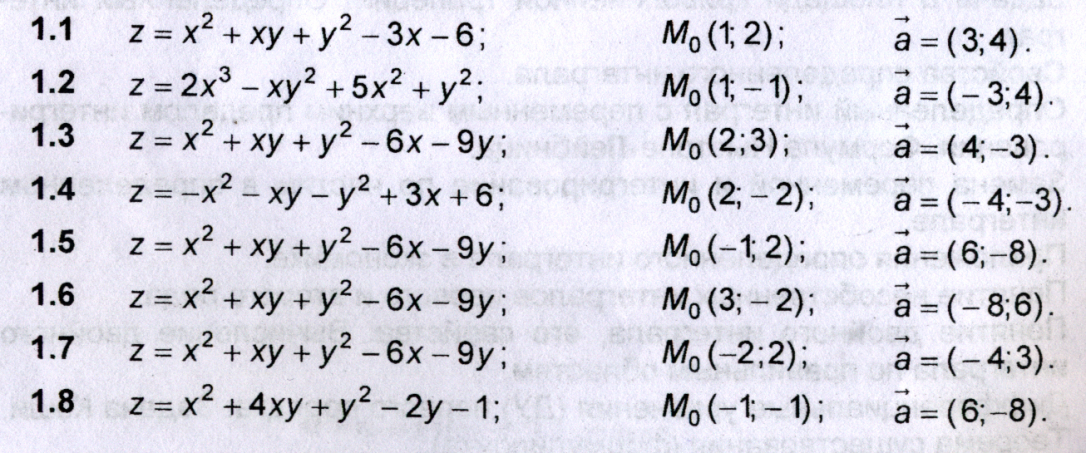
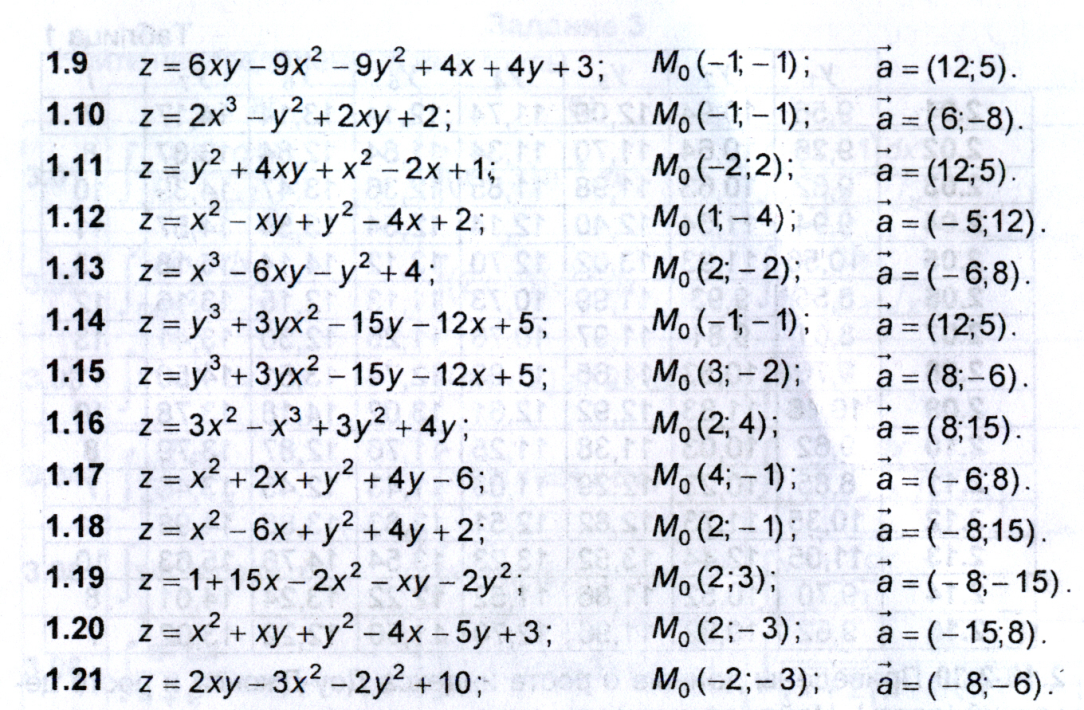
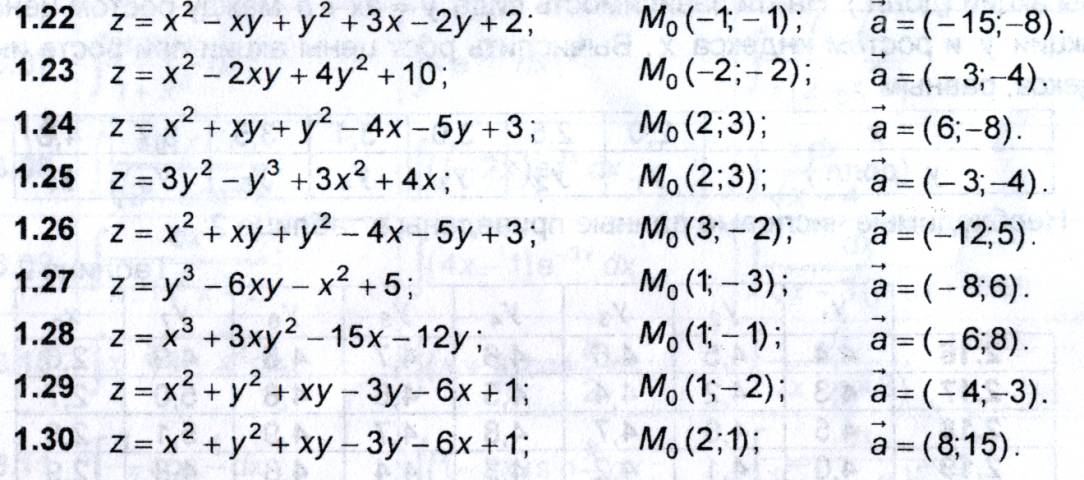
Задание 2
Используя
метод наименьших квадратов, найти
линейную зависимость между
![]() и
и
![]() по данным, приведенным в таблице. Сделать
чертеж.
по данным, приведенным в таблице. Сделать
чертеж.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−9 |
−7 |
−2 |
−1 |
3 |
−3 |
9 |
11 |
15 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−9 |
−8 |
−4 |
−4 |
−1 |
−8 |
3 |
4 |
7 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
−5 |
−4 |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
|
−15 |
−13 |
−8 |
−7 |
−3 |
−9 |
3 |
5 |
9 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
|
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
−3 |
−2 |
2 |
2 |
5 |
−2 |
9 |
10 |
13 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−9 |
−7 |
−2 |
−1 |
3 |
−3 |
9 |
11 |
15 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−6 |
−4 |
1 |
2 |
6 |
0 |
12 |
14 |
18 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−4 |
−4 |
−1 |
−2 |
0 |
−8 |
2 |
2 |
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10) |
|
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
11) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−9 |
−7 |
−2 |
−1 |
3 |
−3 |
9 |
11 |
15 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−9 |
−8 |
−4 |
−4 |
−1 |
−8 |
3 |
4 |
7 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
13) |
|
−5 |
−4 |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
|
−15 |
−13 |
−8 |
−7 |
−3 |
−9 |
3 |
5 |
9 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15) |
|
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
−3 |
−2 |
2 |
2 |
5 |
−2 |
9 |
10 |
13 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
16) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−9 |
−7 |
−2 |
−1 |
3 |
−3 |
9 |
11 |
15 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
17) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−6 |
−4 |
1 |
2 |
6 |
0 |
12 |
14 |
18 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
18) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−4 |
−4 |
−1 |
−2 |
0 |
−8 |
2 |
2 |
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
19) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
20) |
|
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
221) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−9 |
−7 |
−2 |
−1 |
3 |
−3 |
9 |
11 |
15 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
22) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−9 |
−8 |
−4 |
−4 |
−1 |
−8 |
3 |
4 |
7 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
23) |
|
−5 |
−4 |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
|
−15 |
−13 |
−8 |
−7 |
−3 |
−9 |
3 |
5 |
9 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
24) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
25) |
|
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
−3 |
−2 |
2 |
2 |
5 |
−2 |
9 |
10 |
13 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
26) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−9 |
−7 |
−2 |
−1 |
3 |
−3 |
9 |
11 |
15 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
27) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−6 |
−4 |
1 |
2 |
6 |
0 |
12 |
14 |
18 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
28) |
|
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
−4 |
−4 |
−1 |
−2 |
0 |
−8 |
2 |
2 |
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
29) |
|
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
30) |
|
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
−4 |
−3 |
1 |
1 |
4 |
−3 |
8 |
9 |
12 |
15 |
Задание 3
Найти неопределенные интегралы:
1
а)
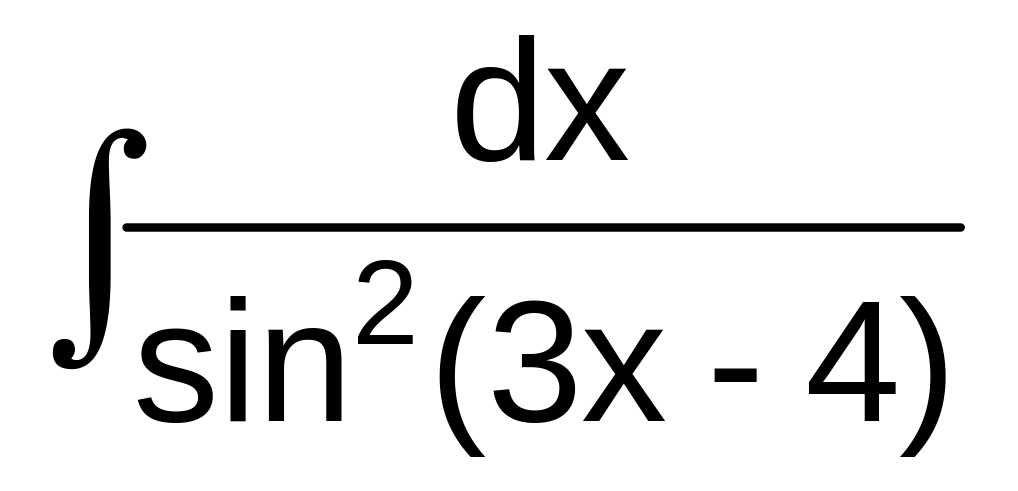 б)
б)
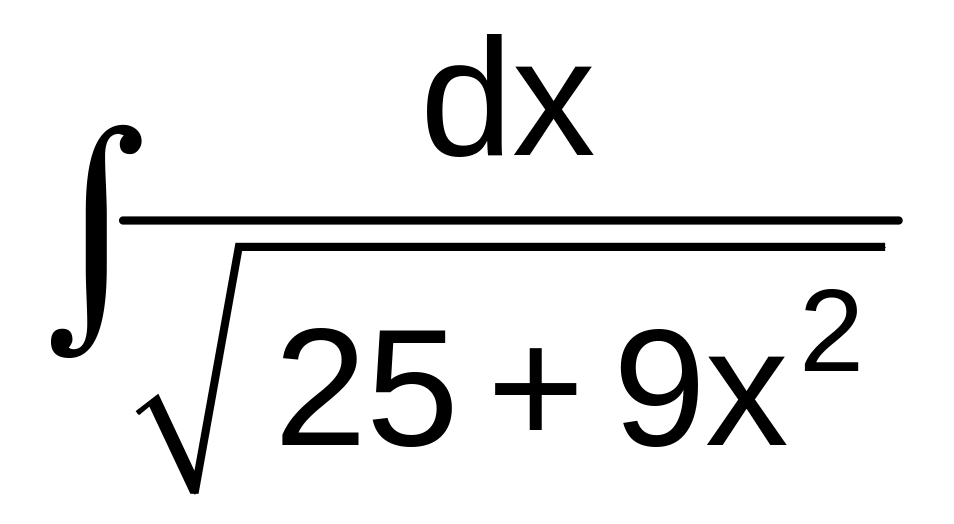 в)
в)
![]() г)
г)

2
а)
![]() б)
б)
![]() в)
в)
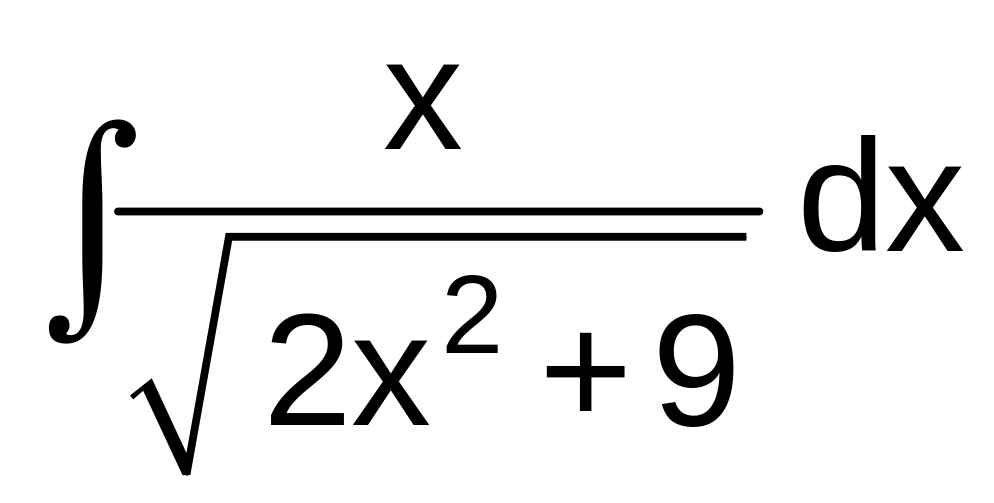 г)
г)
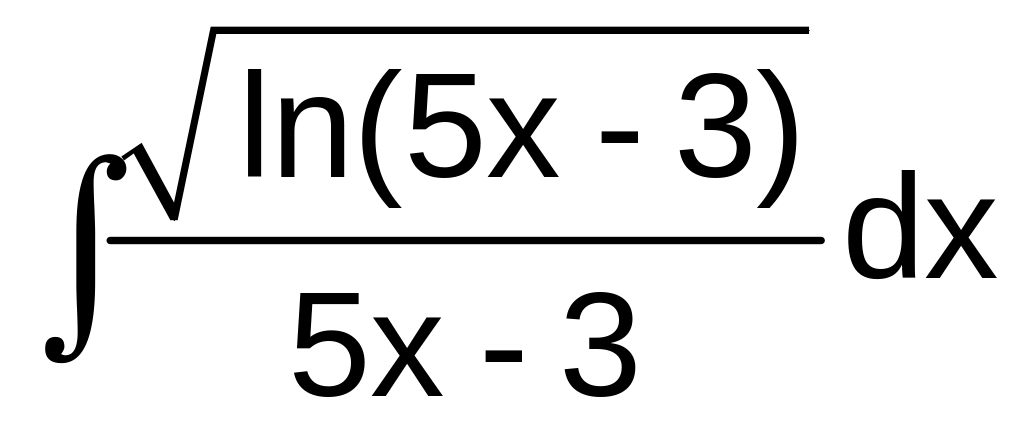
3
а)
![]() б)
б)
![]() в)
г)
в)
г)
4
а)
![]() б)
б)
![]() в)
в)
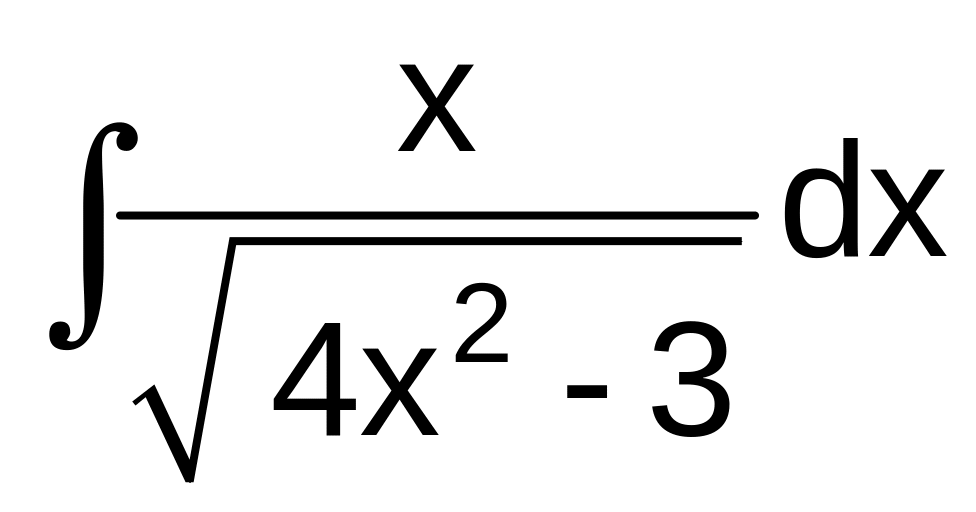 г)
г)
![]()
5
а)
![]() б)
б)
 в)
в)
![]() г)
г)
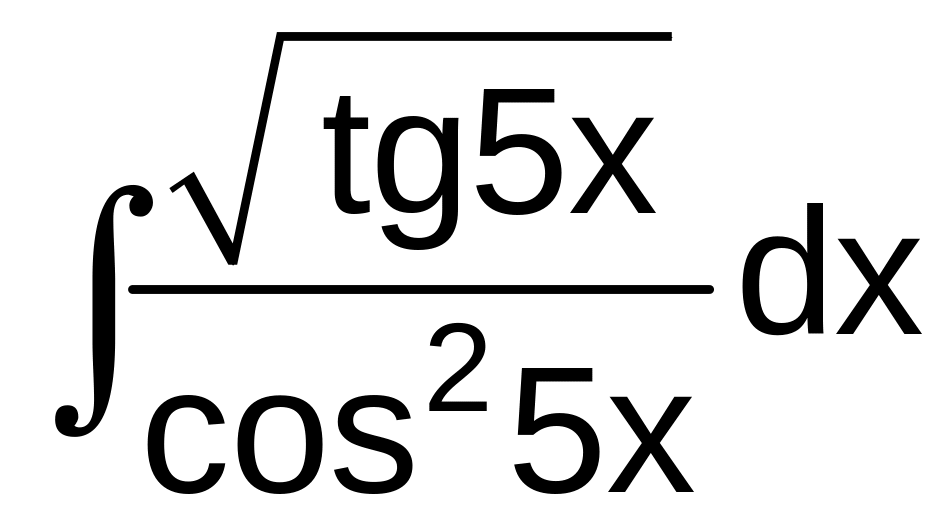
6
а)
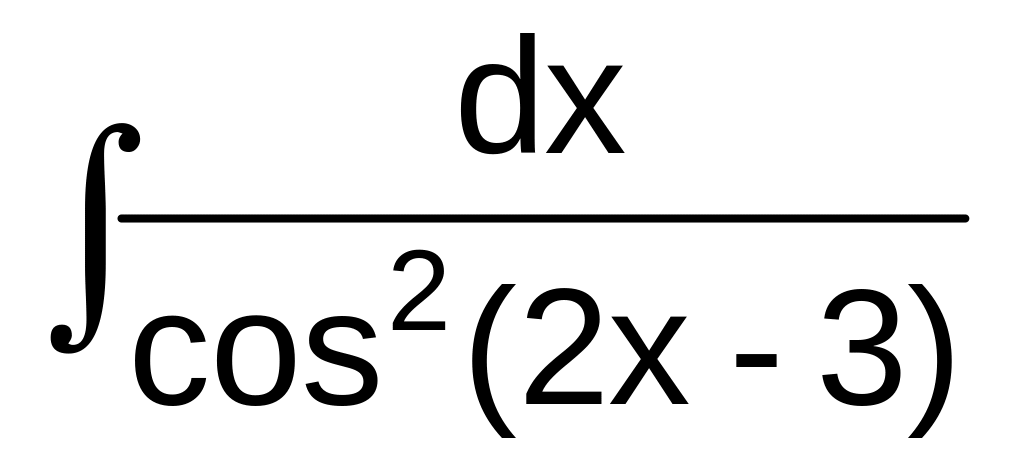 б)
б)
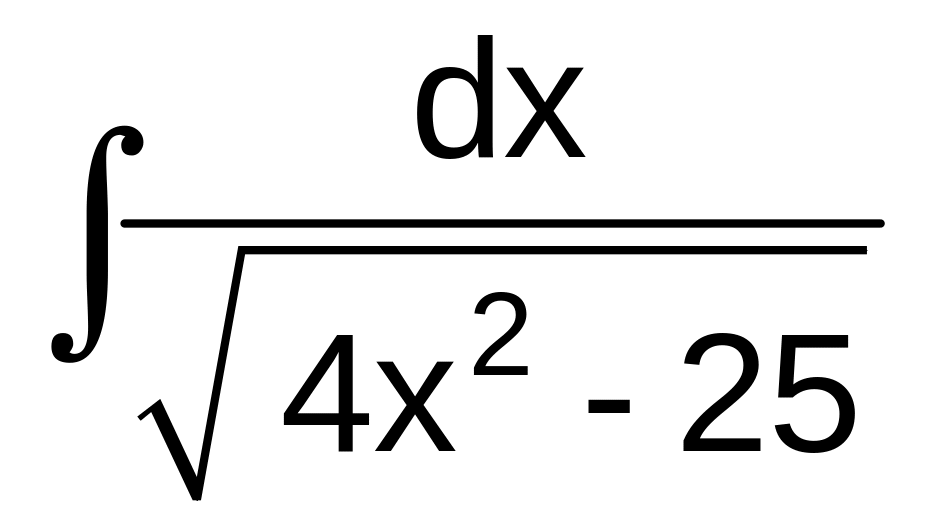 в)
в)
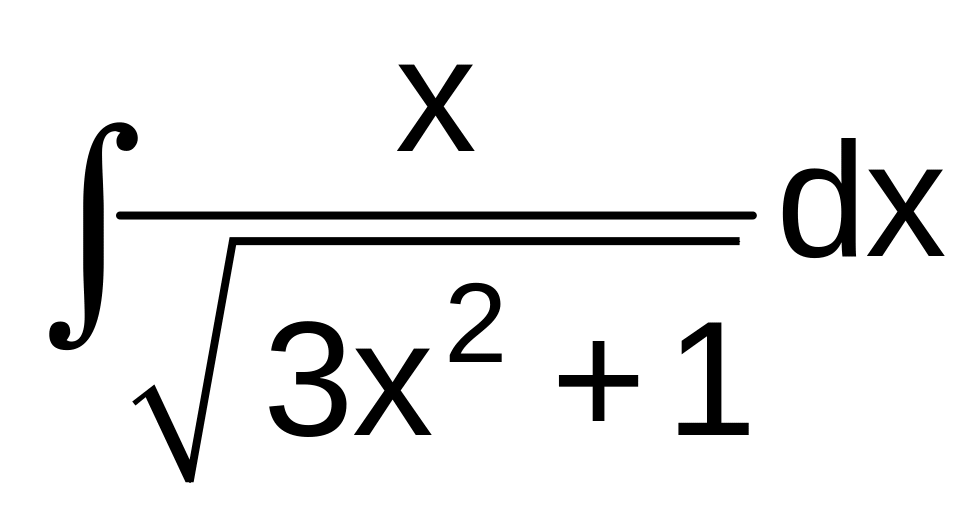 г)
г)
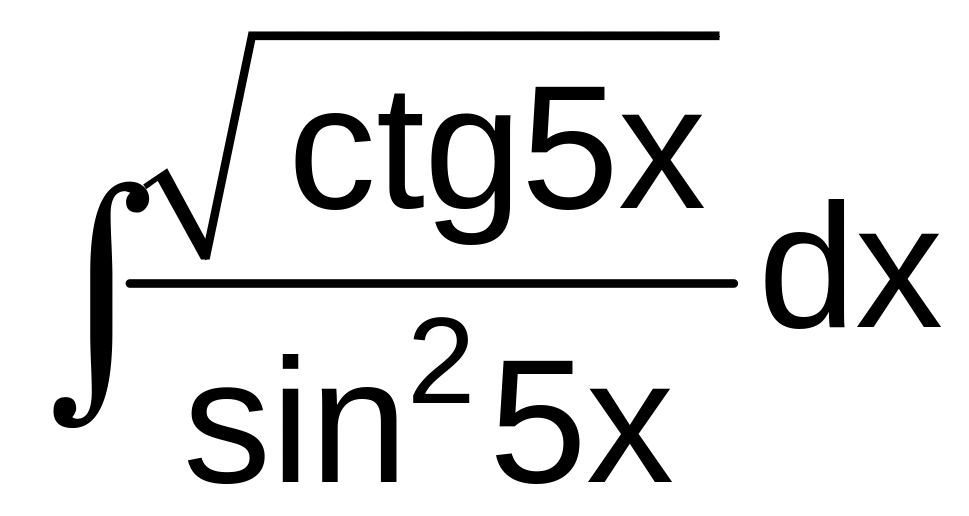
7
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
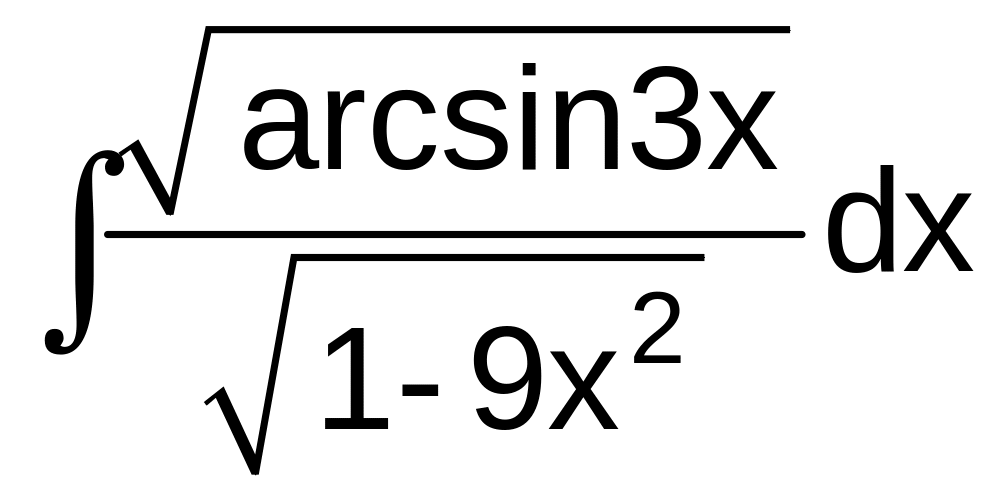
8
а)
![]() б)
б)
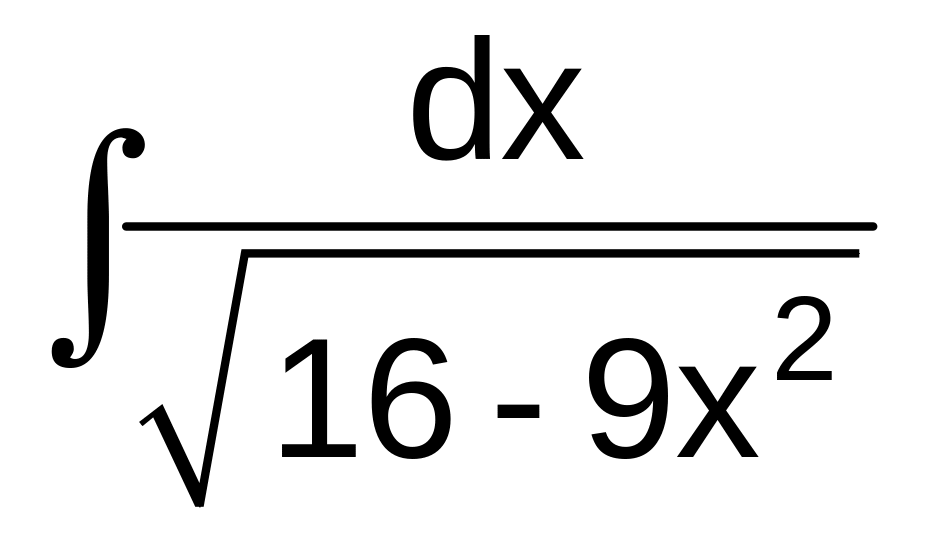 в)
в)
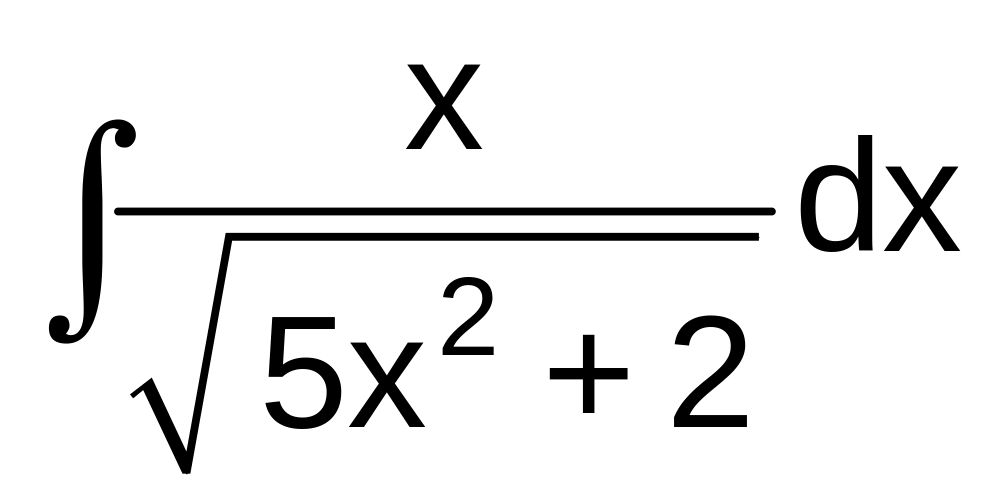 г)
г)
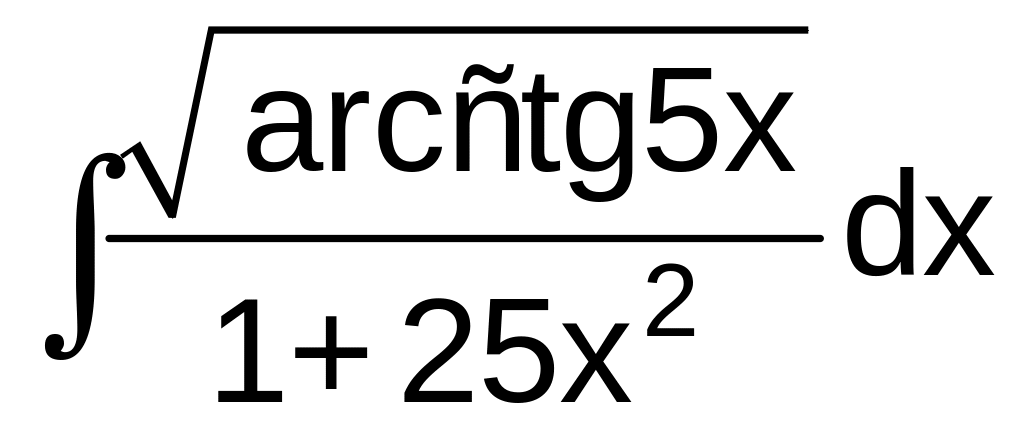
9
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)

10
а)
![]() б)
б)
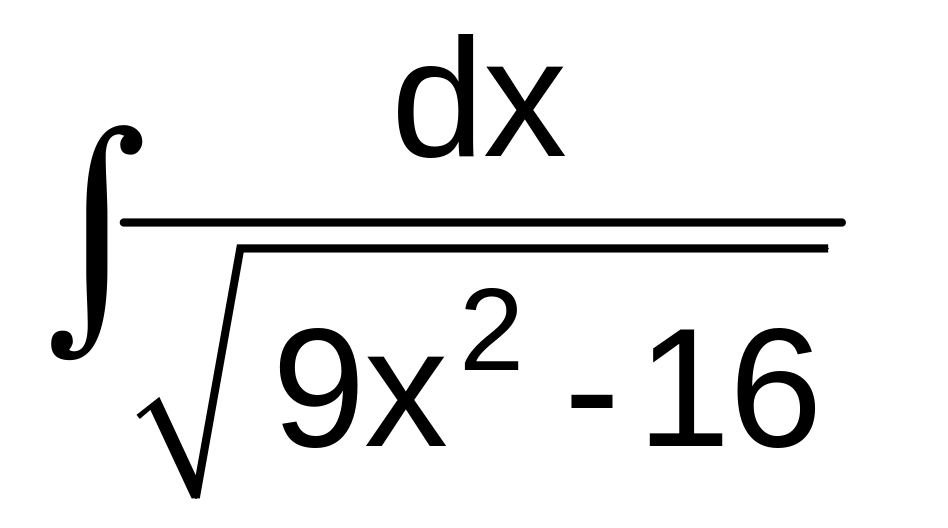 в)
в)
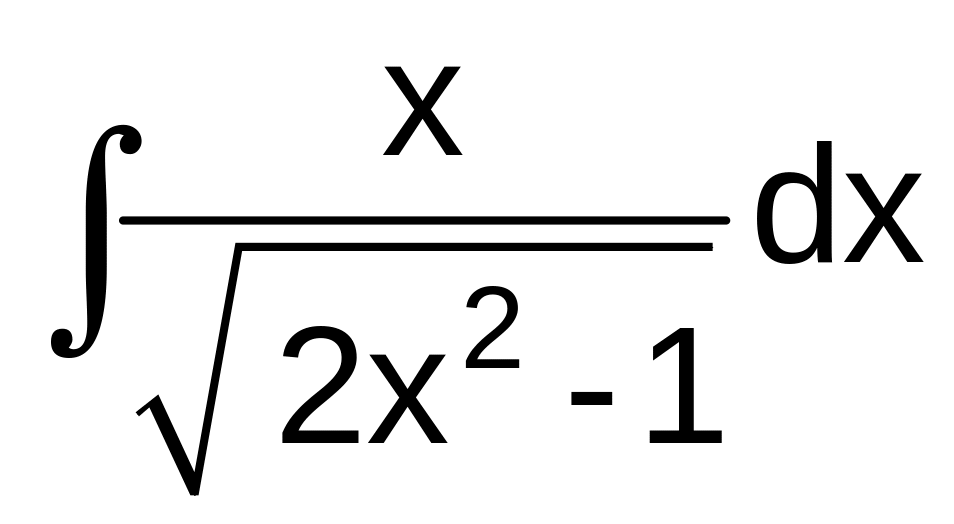 г)
г)
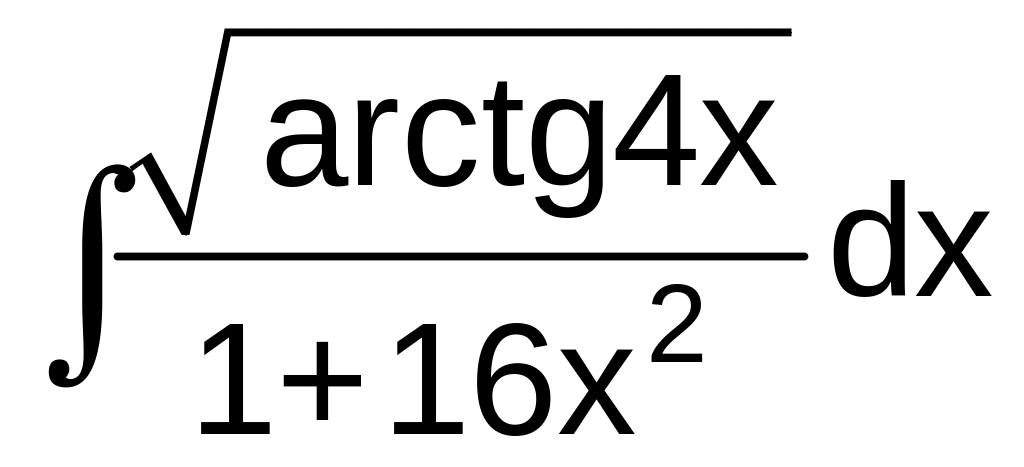
11 а) б) в) г)
12 а) б) в) г)
13 а) б) в) г)
14 а) б) в) г)
15 а) б) в) г)
16 а) б) в) г)
17 а) б) в) г)
18 а) б) в) г)
19 а) б) в) г)
20 а) б) в) г)
21 а) б) в) г)
22 а) б) в) г)
23 а) б) в) г)
24 а) б) в) г)
25 а) б) в) г)
26 а) б) в) г)
27 а) б) в) г)
28 а) б) в) г)
29 а) б) в) г)
30 а) б) в) г)
Задание 4
Найти неопределенный интеграл
1
а)
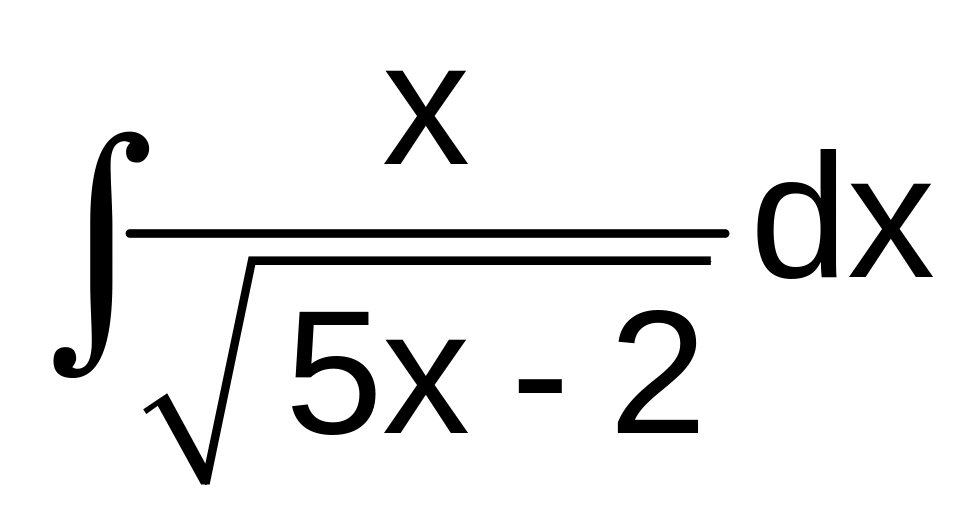 б)
б)
![]() в)
в)
![]()
2
а)
 б)
б)
![]() в)
в)
![]()
3
а)
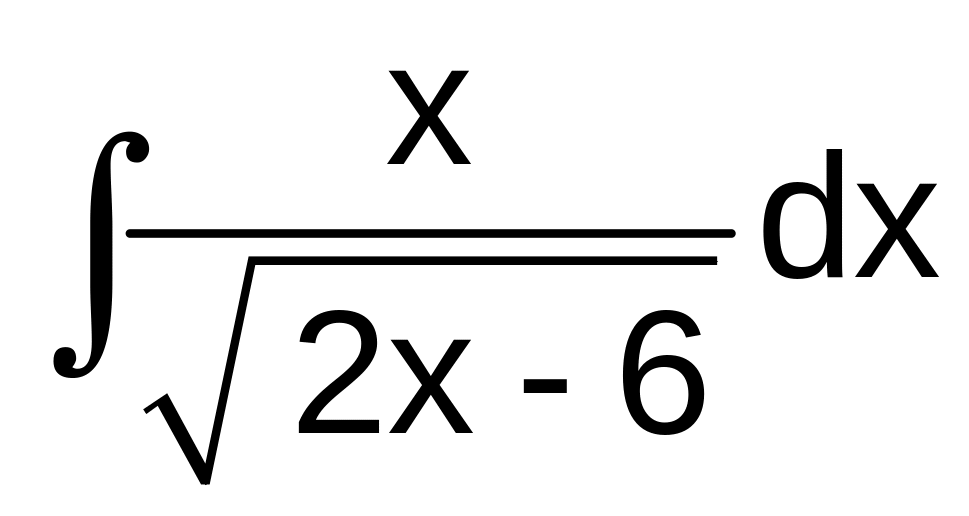 б)
б)
![]() в)
в)
![]()
4
а)
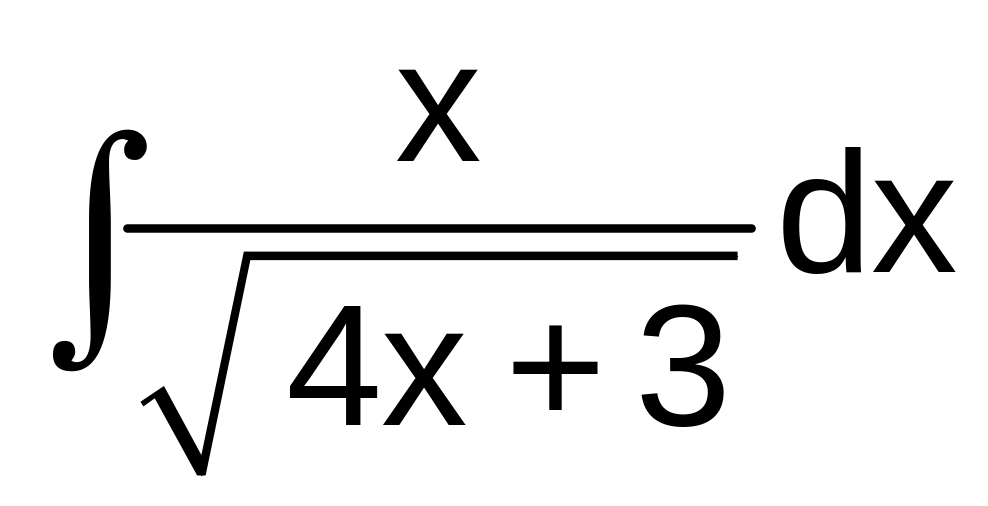 б)
б)
![]() в)
в)
![]()
5
а)
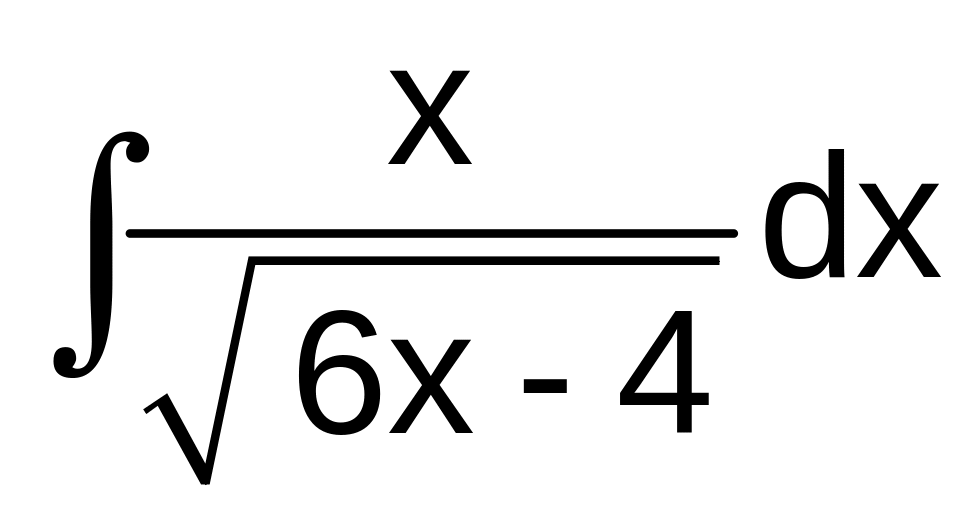 б)
б)
![]() в)
в)
![]()
6
а)
![]() б)
б)
![]() в)
в)
![]()
7
а)
![]() б)
б)
![]() в)
в)
![]()
8
а)
![]() б)
б)
![]() в)
в)
![]()
9
а)
![]() б)
б)
![]() в)
в)
![]()
10
а)
![]() б)
б)
![]() в)
в)
![]()
11 а) б) в)
12 а) б) в)
13 а) б) в)
14 а) б) в)
15 а) б) в)
16 а) б) в)
17 а) б) в)
18 а) б) в)
19 а) б) в)
20 а) б) в)
21 а) б) в)
22 а) б) в)
23 а) б) в)
24 а) б) в)
25 а) б) в)
26 а) б) в)
27 а) б) в)
28 а) б) в)
29 а) б) в)
30 а) б) в)
Задание 5
Найти площадь фигуры, ограниченной параболой и прямой
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
|
11. |
, |
. |
12. |
, |
. |
13. |
, |
. |
14. |
, |
. |
15. |
, |
. |
16. |
, |
. |
17. |
, |
. |
18. |
, |
. |
19. |
, |
. |
20. |
, |
. |
21. |
, |
. |
22. |
, |
. |
23. |
, |
. |
24. |
, |
. |
25. |
, |
. |
26. |
, |
. |
27. |
, |
. |
28. |
, |
. |
29. |
, |
. |
30. |
, |
. |
Задание 6
Найти общее решение дифференциального уравнения:
№ |
а) |
б) |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
. |
. |
12 |
. |
. |
13 |
. |
. |
14 |
. |
. |
15 |
. |
. |
16 |
. |
. |
17 |
. |
. |
18 |
. |
. |
19 |
. |
. |
20 |
. |
. |
21 |
. |
. |
22 |
. |
. |
23 |
. |
. |
24 |
. |
. |
25 |
. |
. |
26 |
. |
. |
27 |
. |
. |
28 |
. |
. |
29 |
. |
. |
30 |
. |
. |
№ 7 Найти частное решение дифференциального уравнения:
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
. |
8 |
|
. |
9 |
|
. |
10 |
|
|
11 |
, |
. |
12 |
, |
. |
13 |
, |
. |
14 |
, |
. |
15 |
. |
. |
16 |
, |
. |
17 |
, |
. |
18 |
, |
. |
19 |
, |
. |
20 |
, |
. |
21 |
, |
. |
22 |
, |
. |
23 |
, |
. |
24 |
, |
. |
25 |
. |
. |
26 |
, |
. |
27 |
, |
. |
28 |
, |
. |
29 |
, |
. |
30 |
, |
. |
№8 Найти общее решение дифференциального уравнения:
1 |
а)
|
б)
|
в)
|
2 |
а)
|
б)
|
в)
|
3 |
а)
|
б)
|
в)
|
4 |
а)
|
б)
|
в)
|
5 |
а)
|
б)
|
в)
|
6 |
а)
|
б)
|
в)
|
7 |
а)
|
б)
|
в)
|
8 |
а)
|
б)
|
в)
|
9 |
а)
|
б) |
в)
|
10 |
а)
|
б)
|
в)
|
11 |
а) , |
б) , |
в) . |
12 |
а) , |
б) , |
в) . |
13 |
а) , |
б) , |
в) . |
14 |
а) , |
б) , |
в) . |
15 |
а) , |
б) , |
в) . |
16 |
а) , |
б) , |
в) . |
17 |
а) , |
б) , |
в) . |
18 |
а) , |
б) , |
в) . |
19 |
а) , |
б) , |
в) . |
20 |
а) , |
б) , |
в) . |
21 |
а) , |
б) , |
в) . |
22 |
а) , |
б) , |
в) . |
23 |
а) , |
б) , |
в) . |
24 |
а) , |
б) , |
в) . |
25 |
а) , |
б) , |
в) . |
26 |
а) , |
б) , |
в) . |
27 |
а) , |
б) , |
в) . |
28 |
а) , |
б) , |
в) . |
29 |
а) , |
б) , |
в) . |
30 |
а) , |
б) , |
в) . |
№9 . Найти общее решение дифференциального уравнения:
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
. |
12 |
. |
13 |
. |
14 |
. |
15 |
. |
16 |
. |
17 |
. |
18 |
. |
19 |
. |
20 |
. |
21 |
. |
22 |
. |
23 |
. |
24 |
. |
25 |
. |
26 |
. |
27 |
. |
28 |
. |
29 |
. |
30 |
. |
№10 Найти общее решение дифференциального уравнения
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
. |
12 |
. |
13 |
. |
14 |
. |
15 |
. |
16 |
. |
17 |
. |
18 |
. |
19 |
. |
20 |
. |
21 |
. |
22 |
. |
23 |
. |
24 |
. |
25 |
. |
26 |
. |
27 |
. |
28 |
. |
29 |
. |
30 |
. |
№11 Исследовать сходимость ряда:
№ |
а) |
б) |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
. |
. |
12 |
. |
. |
13 |
. |
. |
14 |
. |
. |
15 |
. |
. |
16 |
. |
. |
17 |
. |
. |
18 |
. |
. |
19 |
. |
. |
20 |
. |
. |
21 |
. |
. |
22 |
. |
. |
23 |
. |
. |
24 |
. |
. |
25 |
. |
. |
26 |
. |
. |
27 |
. |
. |
28 |
. |
. |
29 |
. |
. |
30 |
. |
. |
№12 Исследовать сходимость ряда:
№ |
а) |
б) |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
. |
9 |
|
|
10 |
|
|
11 |
|
. |
12 |
|
. |
13 |
|
. |
14 |
|
. |
15 |
|
. |
16 |
|
. |
17 |
|
. |
18 |
|
. |
19 |
|
. |
20 |
|
. |
21 |
|
. |
22 |
|
. |
23 |
|
. |
24 |
|
. |
25 |
|
. |
26 |
|
. |
27 |
|
. |
28 |
|
. |
29 |
|
. |
30 |
|
. |
№13 Найти область сходимости степенного ряда:
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
. |
12 |
. |
13 |
. |
14 |
. |
15 |
. |
16 |
. |
17 |
. |
18 |
. |
19 |
. |
20 |
. |
21 |
. |
22 |
. |
23 |
. |
24 |
. |
25 |
. |
26 |
. |
27 |
. |
28 |
. |
29 |
. |
30 |
. |
Рекомендации к решению заданий 6-13:
№6. Найти общее решение дифференциального уравнения:
а)
![]() .
.
Решение.
Исходное уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными.
Заметим,
что
![]() является одним из решений исходного
дифференциального уравнения.
является одним из решений исходного
дифференциального уравнения.
Разделяя переменные, имеем
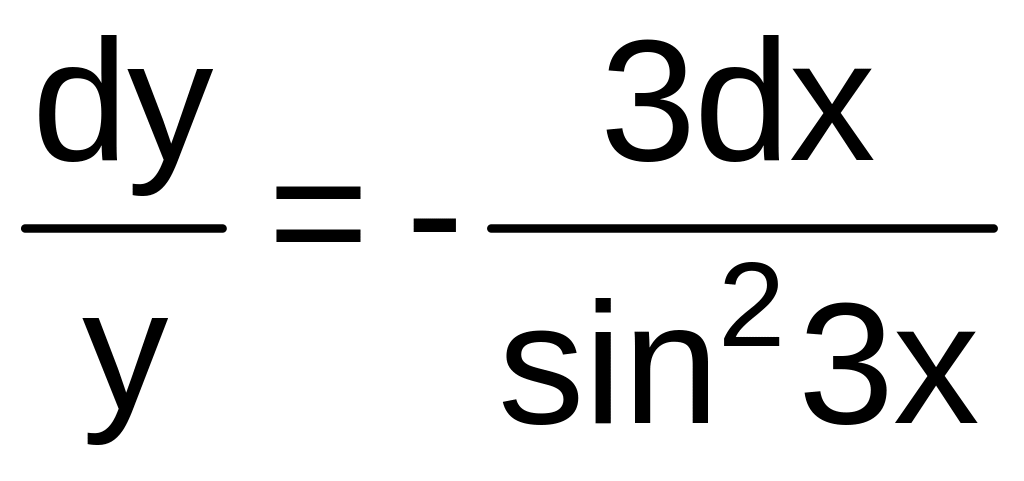 или
или
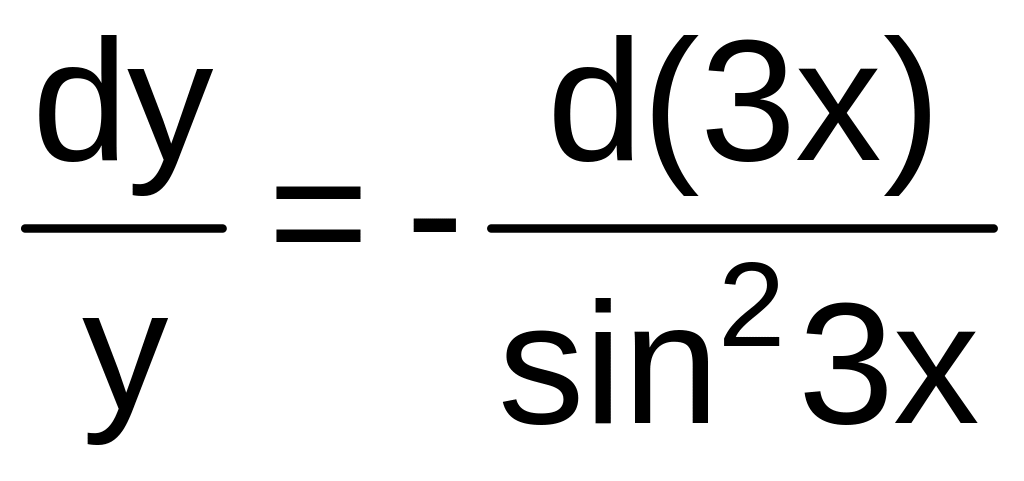 .
.
Интегрируя последнее уравнение, получим
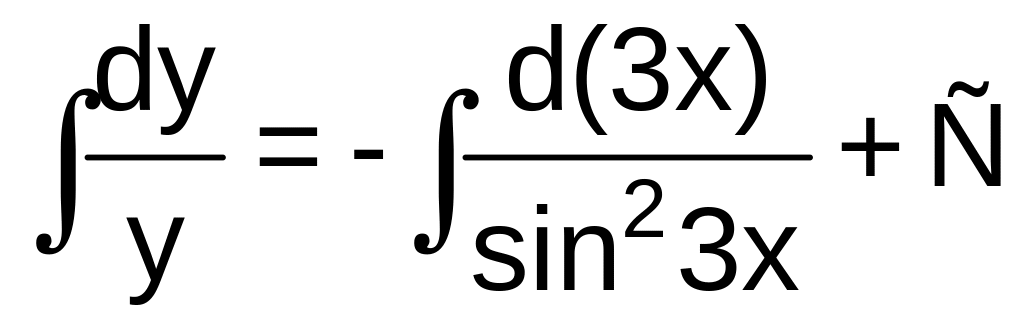 или
или
![]() .
.
Откуда,
![]() или
или
![]() .
Тогда, полагая
.
Тогда, полагая
![]()
![]() и, учитывая, что
также является решением исходного
уравнения, получим
и, учитывая, что
также является решением исходного
уравнения, получим
![]()
![]()
общее решение уравнения
общее решение уравнения
![]() .
.
Ответ:
![]() .
.
б)
![]() .
.
Решение.
Исходное уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными.
Учитывая,
что
![]() ,
получим уравнение
,
получим уравнение
![]() или
или
![]() .
.
Заметим, что является одним из решений исходного дифференциального уравнения.
Разделяя переменные, имеем
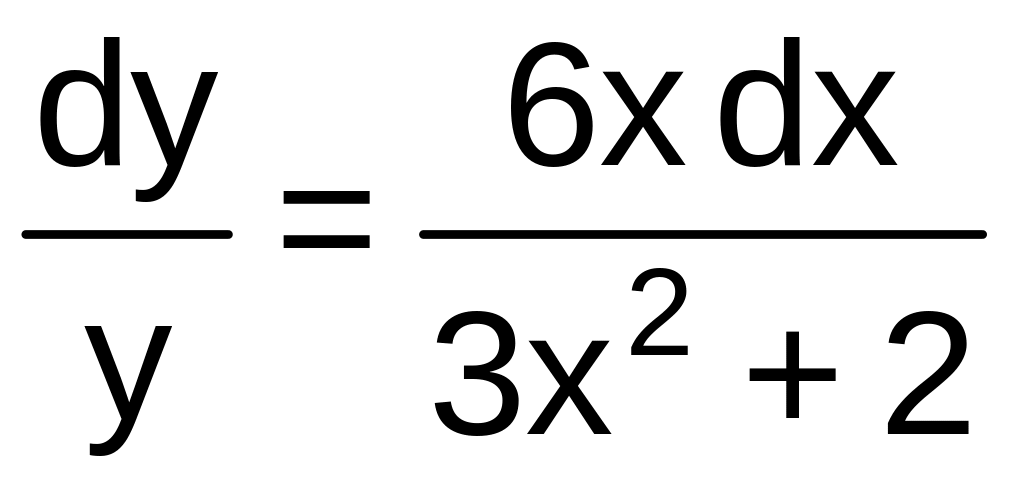 .
.
Интегрируя последнее уравнение, получим
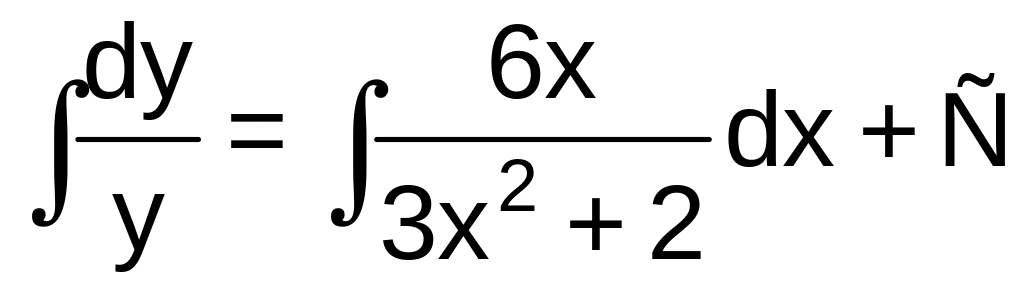 .
.
Учитывая, что
![]() ,
,
имеем
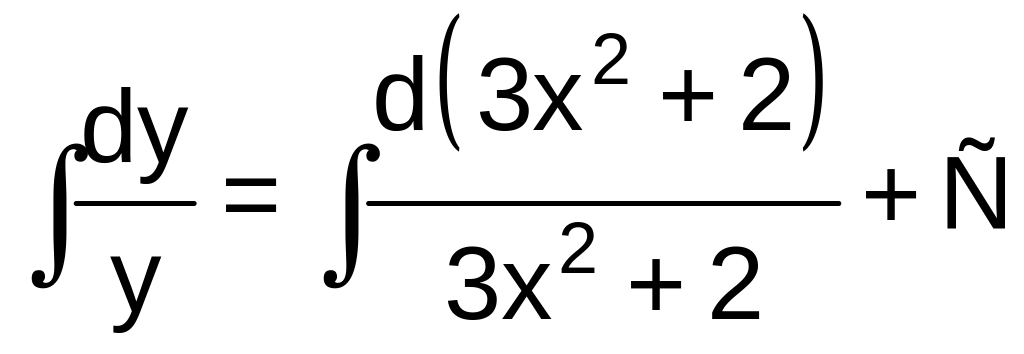 .
.
Откуда,
полагая
![]()
![]() ,
получим
,
получим
![]() .
.
Используя свойства логарифмов, приходим к уравнению
![]() .
.
Откуда
![]() или
или
![]() .
.
Тогда,
полагая
![]()
![]() и, учитывая, что
также является решением исходного
уравнения, получим
и, учитывая, что
также является решением исходного
уравнения, получим
![]() ,
,
![]() ,
,
общее
решение уравнения
![]() .
.
Ответ:
![]() .
.
№7. Найти частное решение дифференциального уравнения:
![]() ,
,
![]() .
.
Решение.
Исходное
уравнение является линейным неоднородным
дифференциальным уравнением первого
порядка вида:
![]() .
Найдем общее решение дифференциального
уравнения методом Бернулли.
.
Найдем общее решение дифференциального
уравнения методом Бернулли.
Решение
уравнения будем искать в виде:
![]() .
Так как
.
Так как
![]() ,
то, подставляя
и
,
то, подставляя
и
![]() в исходное уравнение, получим
в исходное уравнение, получим
![]() .
.
Группируя второе и третье слагаемое в левой части последнего уравнения, имеем
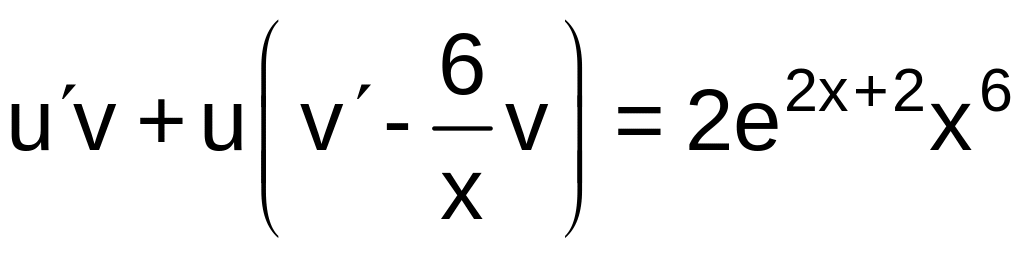 .
.
Найдем
одно из ненулевых решений уравнения
![]() или
или
![]() ,
которое является уравнением с
разделяющимися переменными. Учитывая,
что
,
которое является уравнением с
разделяющимися переменными. Учитывая,
что
![]() ,
имеем
,
имеем
![]() и, разделяя переменные, получим
и, разделяя переменные, получим
![]() .
.
Интегрируя
последнее уравнение, имеем
![]() .
Откуда, полагая
,
получим
.
Откуда, полагая
,
получим
![]() и, используя свойства логарифмов,
приходим к уравнению
и, используя свойства логарифмов,
приходим к уравнению
![]() или
или
![]() .
Откуда
.
Откуда
![]() или
или
![]() .
.
Тогда,
полагая
и, учитывая, что
![]() также является решением уравнения
,
получим
также является решением уравнения
,
получим
![]()
общее решение уравнения
.
общее решение уравнения
.
В
качестве одного из ненулевых решений
возьмем, например
![]() ,
полагая
,
полагая
![]() .
.
Учитывая, что и, подставляя в уравнение
,
получим
![]() или
или
![]()
неполное дифференциальное уравнение
первого порядка вида:
неполное дифференциальное уравнение
первого порядка вида:
![]() .
.
Откуда,
![]() .
.
Учитывая
![]() ,
имеем
,
имеем
![]() .
.
Таким
образом,
![]()
общее решение дифференциального
уравнения.
общее решение дифференциального
уравнения.
Найдем
частное решение, удовлетворяющее
начальному условию
.
Подставляя,
![]() и
и
![]() в уравнение
в уравнение
![]() ,
получим:
,
получим:
![]() или
или
![]() и
и
![]() .
.
Следовательно,
![]()
частное решение исходного дифференциального
уравнения, удовлетворяющее начальному
условию
.
частное решение исходного дифференциального
уравнения, удовлетворяющее начальному
условию
.
Ответ: .
№8. Найти общее решение дифференциального уравнения:
а)
![]() ;
б)
;
в)
;
б)
;
в)
![]() .
.
Решение.
а)
Решим характеристическое уравнение
![]() ,
производя в уравнении
замену
,
производя в уравнении
замену
![]() ,
,
![]() и
и
![]() .
.
Тогда
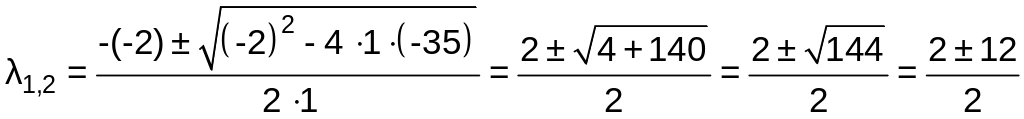 .
.
Откуда
![]() и
и
![]() .
.
Если
характеристическое уравнение имеет
два различных действительных корня
![]() и
и
![]() ,
то общее решение соответствующего
однородного дифференциального уравнения
второго порядка с постоянными
коэффициентами имеет вид
,
то общее решение соответствующего
однородного дифференциального уравнения
второго порядка с постоянными
коэффициентами имеет вид
![]() .
.
Следовательно,
![]()
общее решение исходного уравнения.
общее решение исходного уравнения.
Ответ: .
б)
Решим характеристическое уравнение
![]() ,
производя в уравнении
замену
,
и
.
,
производя в уравнении
замену
,
и
.
Тогда
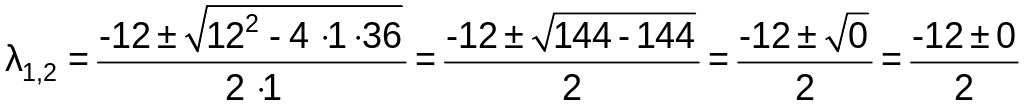 .
.
Откуда
![]() .
.
Если
характеристическое уравнение имеет
два равных действительных корня
![]() (кратный корень), то общее решение
соответствующего однородного
дифференциального уравнения второго
порядка с постоянными коэффициентами
имеет вид
(кратный корень), то общее решение
соответствующего однородного
дифференциального уравнения второго
порядка с постоянными коэффициентами
имеет вид
![]() .
.
Следовательно,
![]()
общее решение исходного уравнения.
общее решение исходного уравнения.
Ответ: .
в)
Решим характеристическое уравнение
![]() ,
производя в уравнении
замену
,
и
.
,
производя в уравнении
замену
,
и
.
Тогда
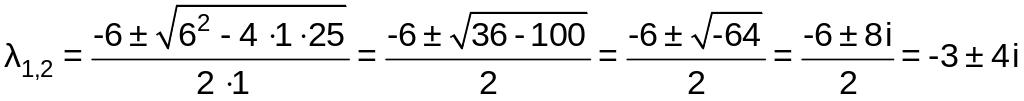 .
.
Откуда
![]() и
и
![]() ,
т.е. корни характеристического уравнения
имеют вид
,
т.е. корни характеристического уравнения
имеют вид
![]() ,
где
,
где
![]() ,
,
![]() .
.
Если
характеристическое уравнение имеет
два сопряженных комплексных корня
![]() и
и
![]() ,
то общее решение соответствующего
однородного дифференциального уравнения
второго порядка с постоянными
коэффициентами имеет вид
,
то общее решение соответствующего
однородного дифференциального уравнения
второго порядка с постоянными
коэффициентами имеет вид
![]() .
.
Следовательно,
![]()
общее решение исходного уравнения.
общее решение исходного уравнения.
Ответ:
![]() .
.
№9. Найти общее решение дифференциального уравнения:
![]() .
.

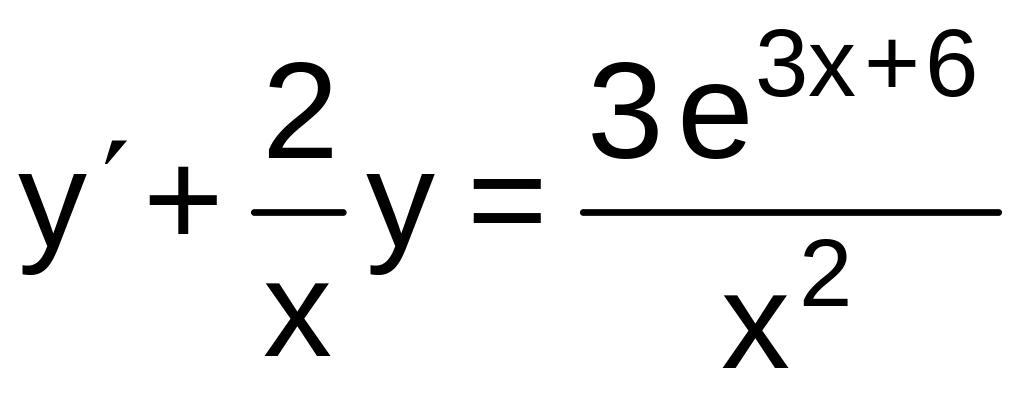 ,
,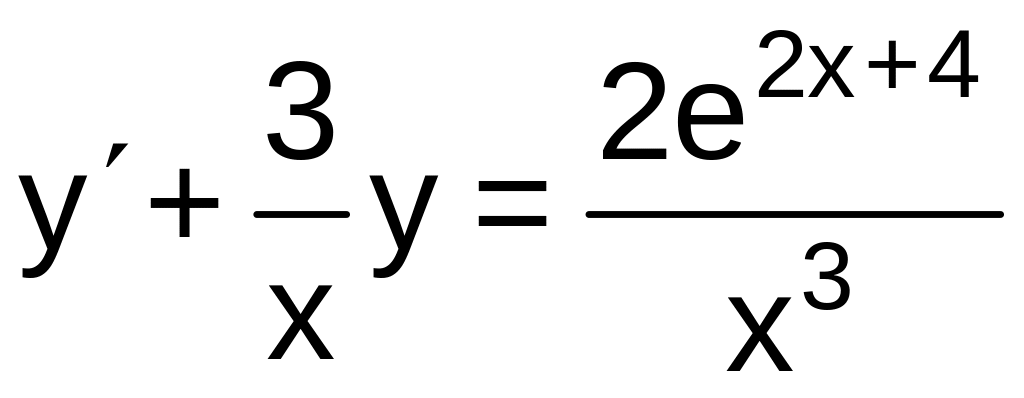 ,
,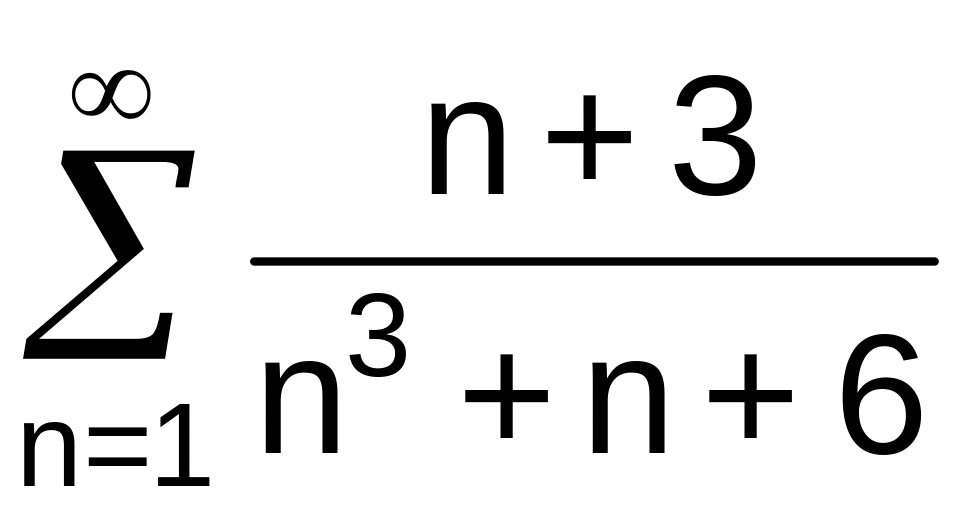 .
.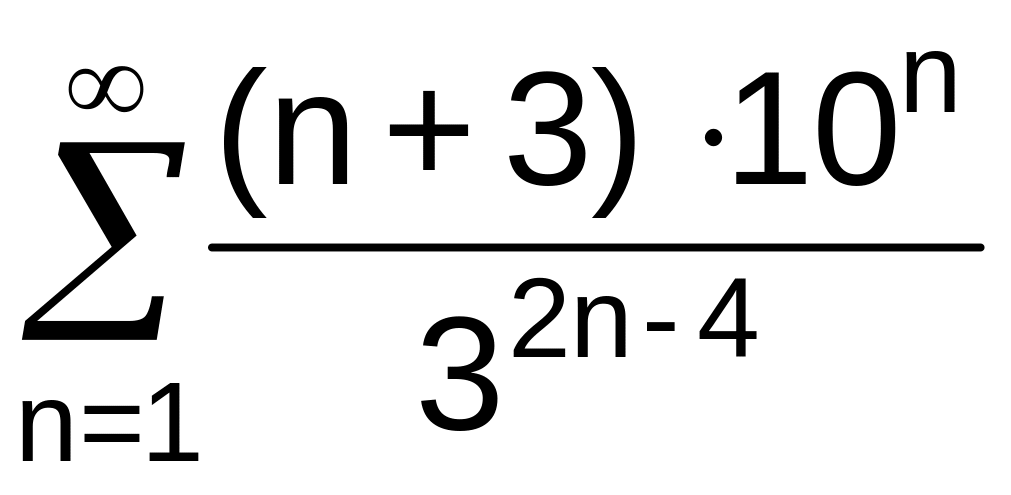 .
.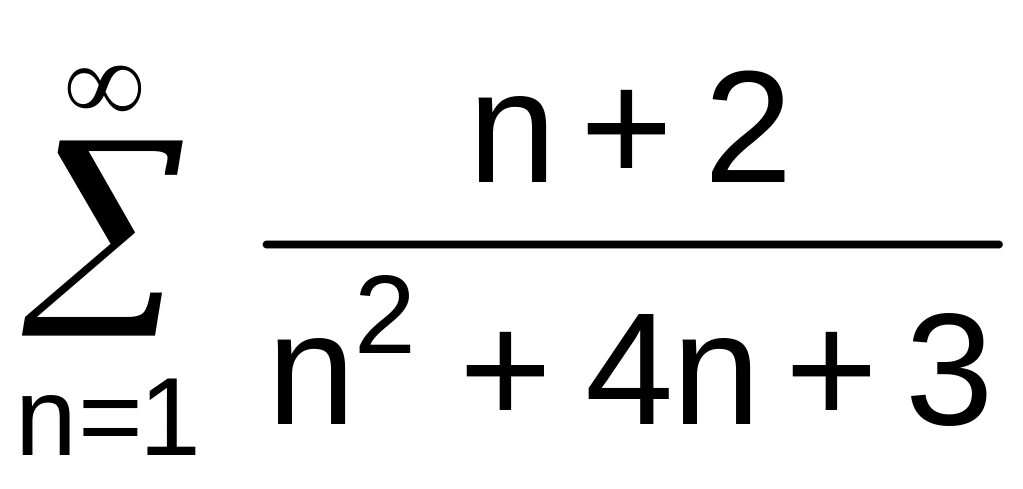 .
.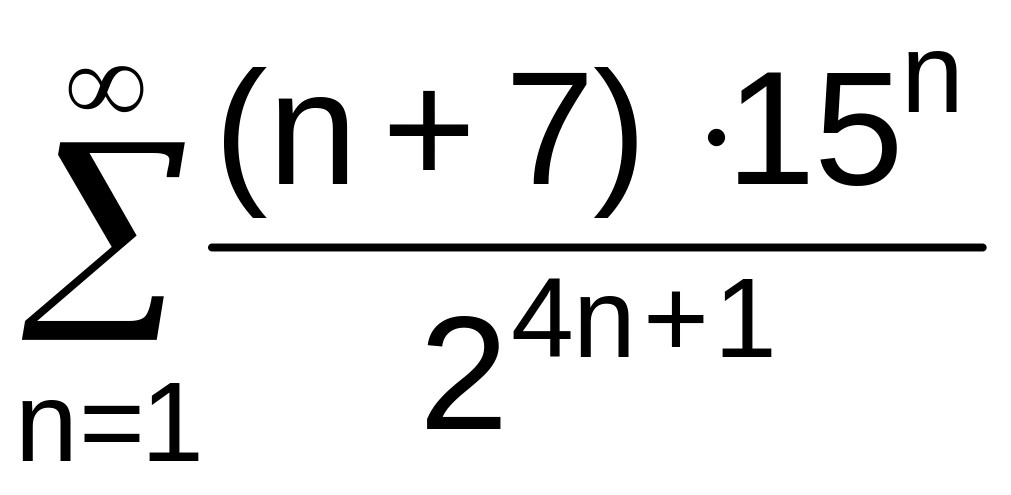 .
. .
.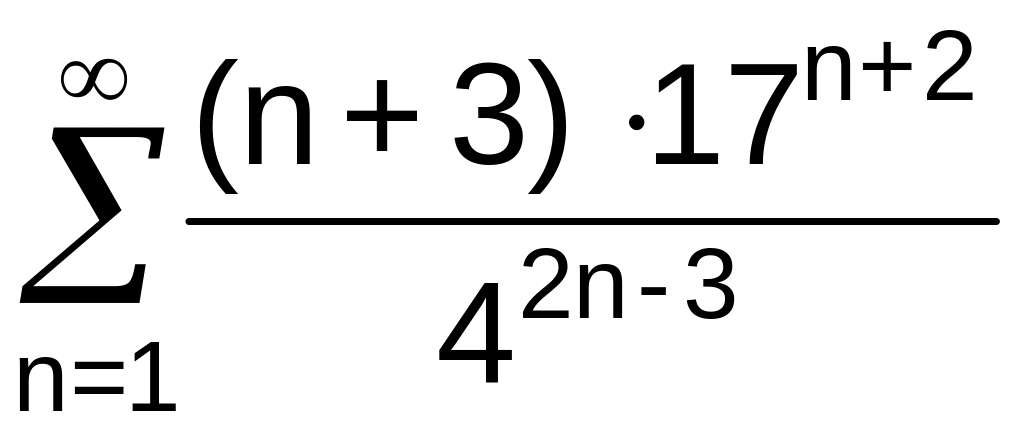 .
.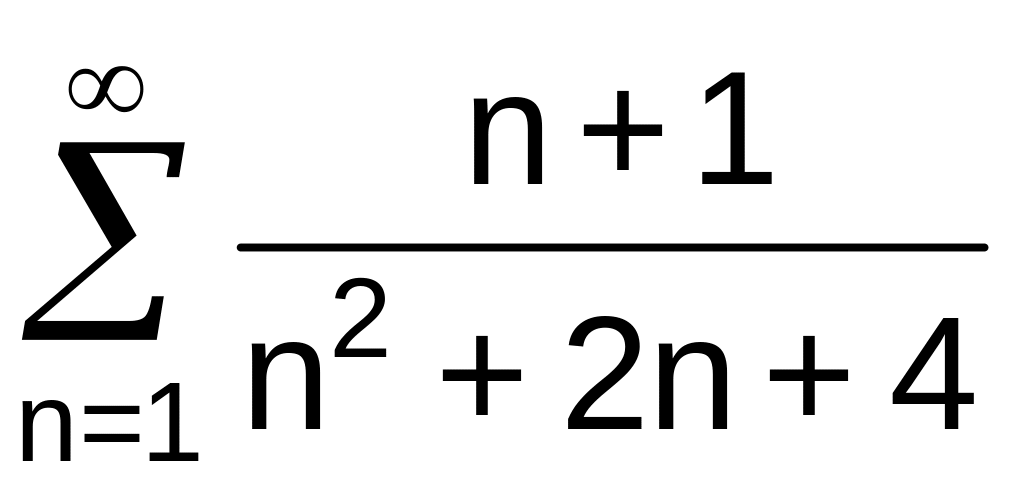 .
.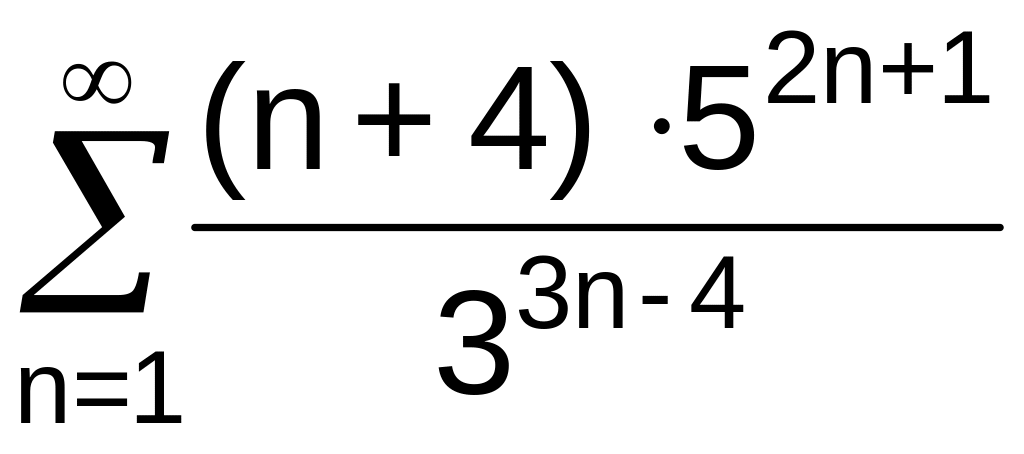 .
.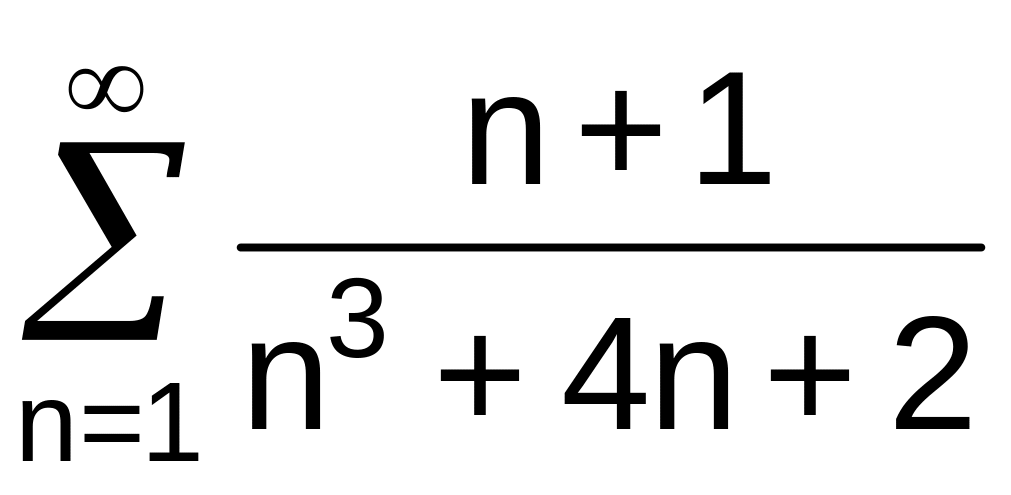 .
.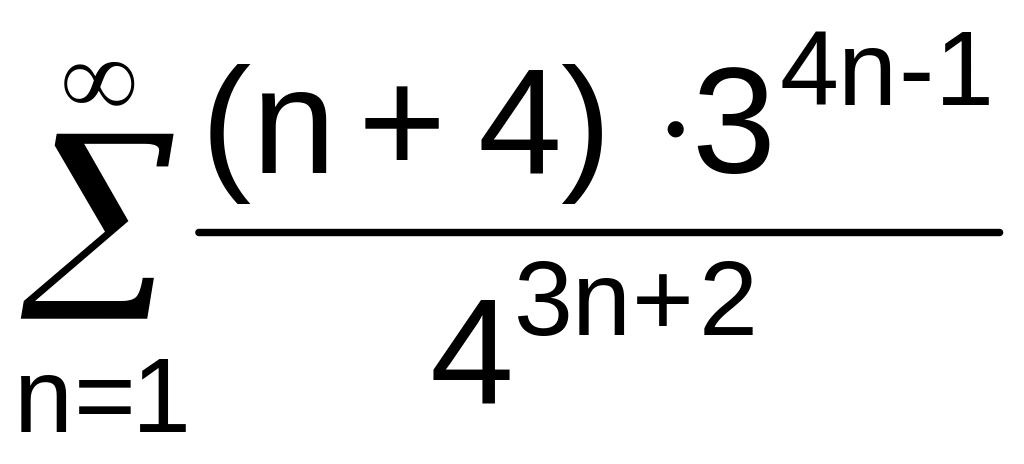 .
.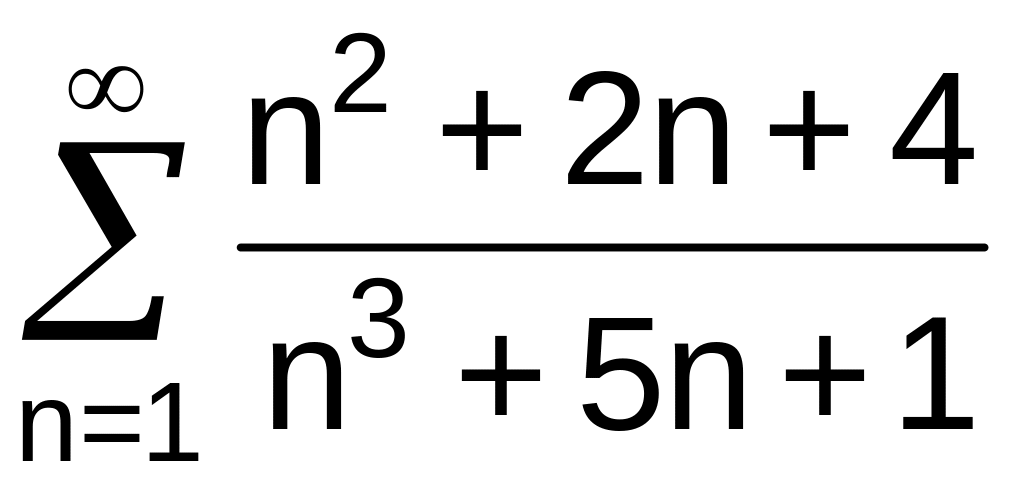 .
.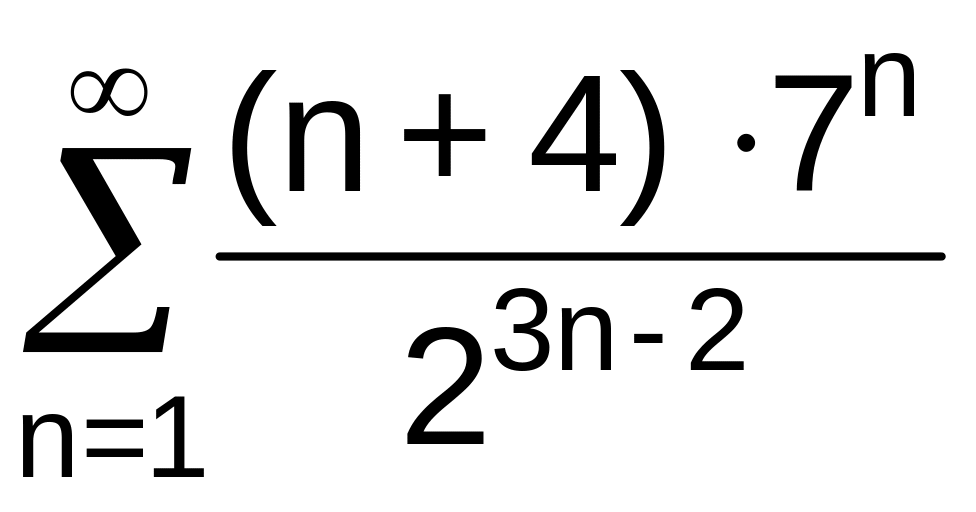 .
.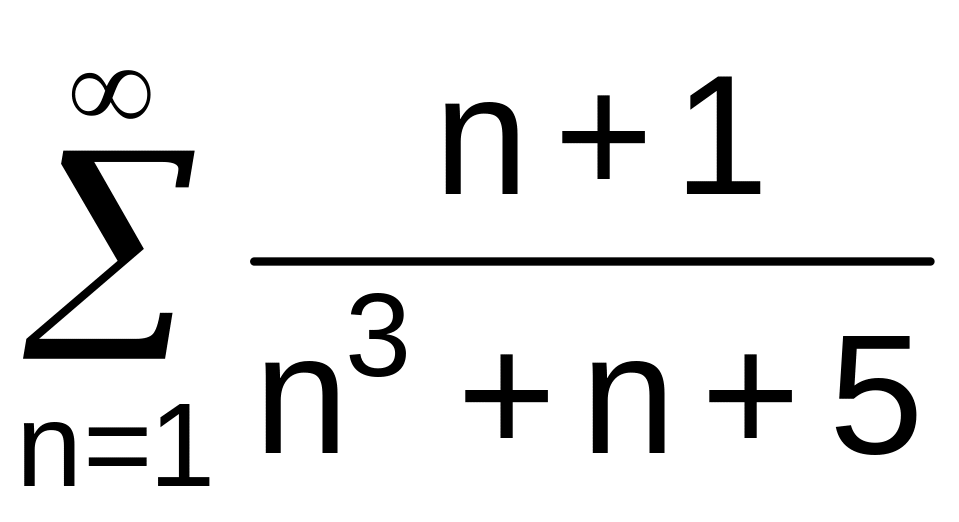 .
.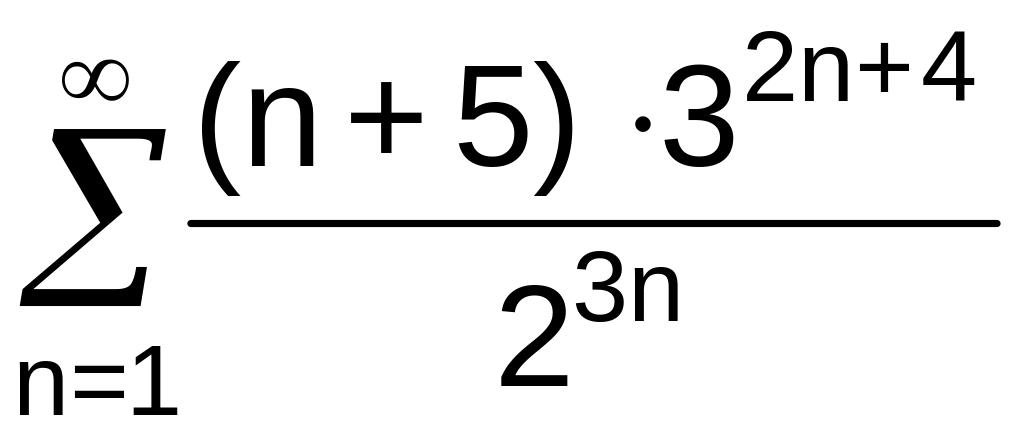 .
.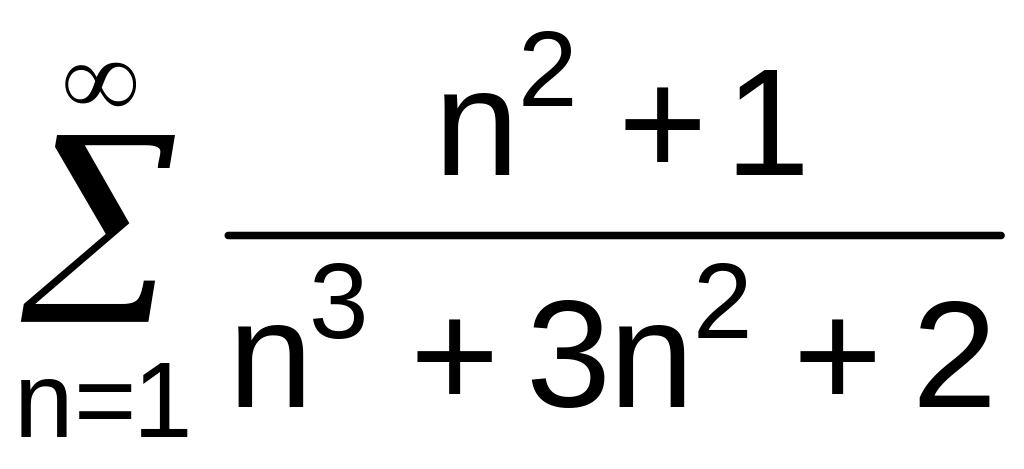 .
.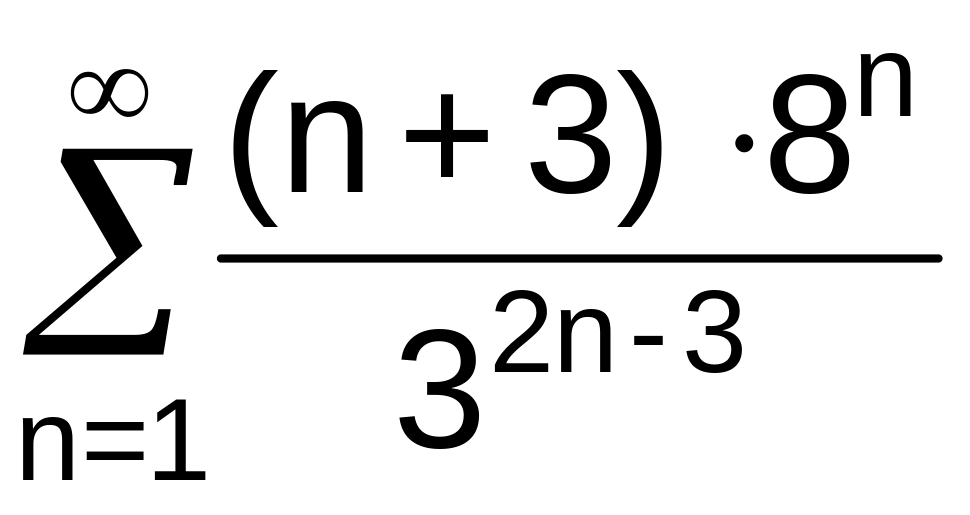 .
.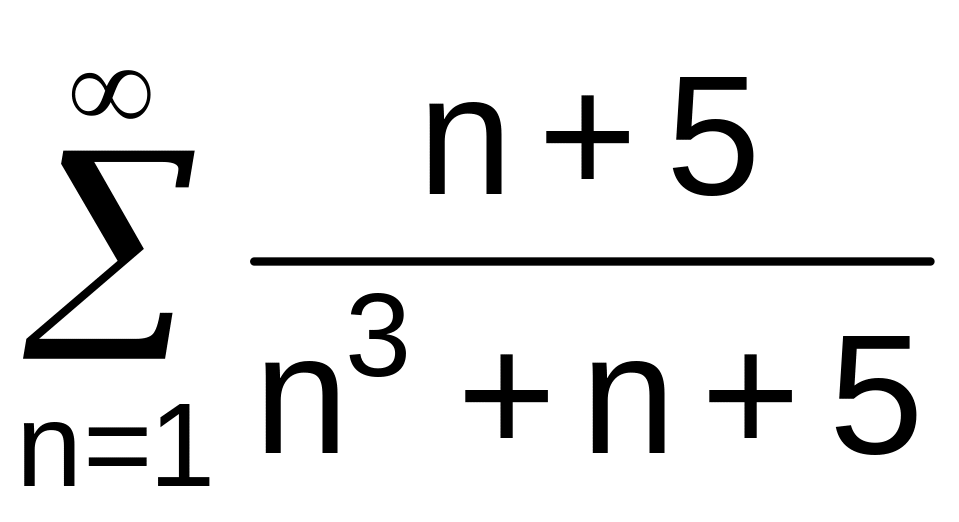 .
. .
.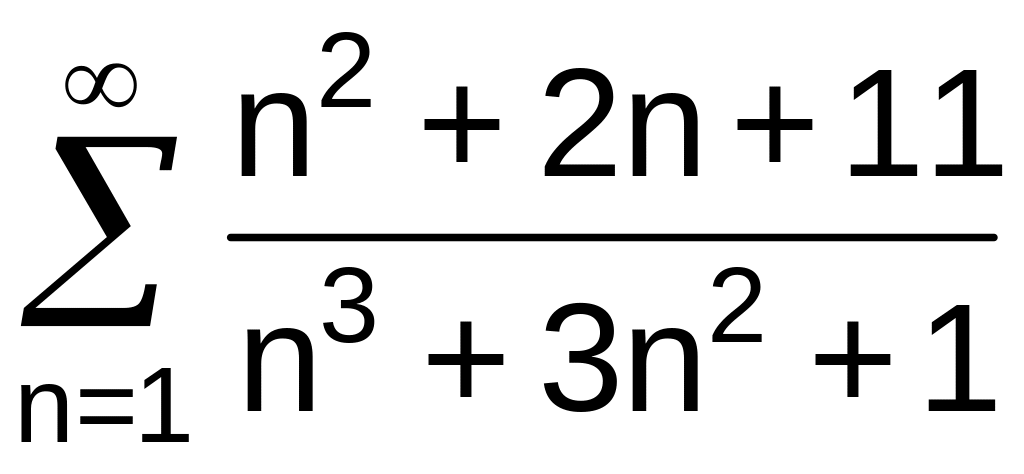 .
.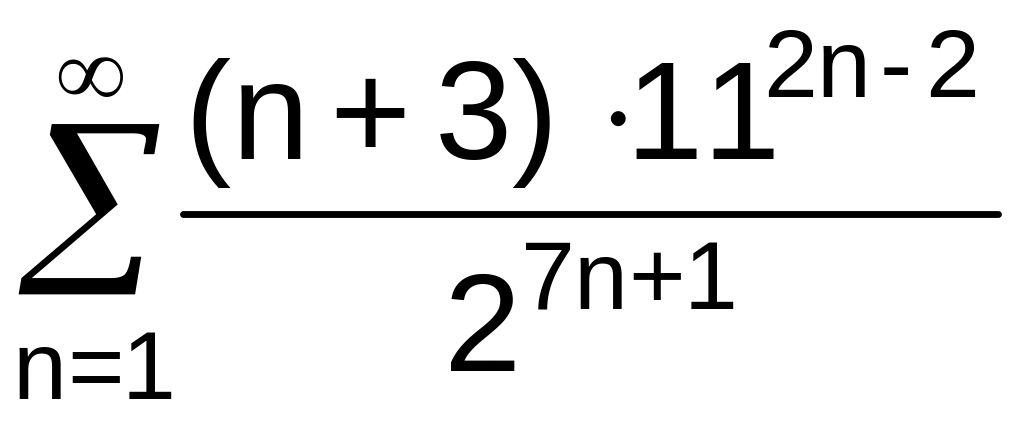 .
.
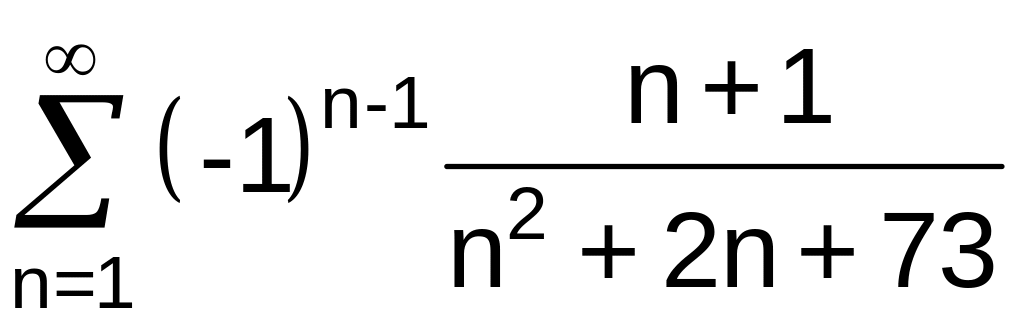 .
.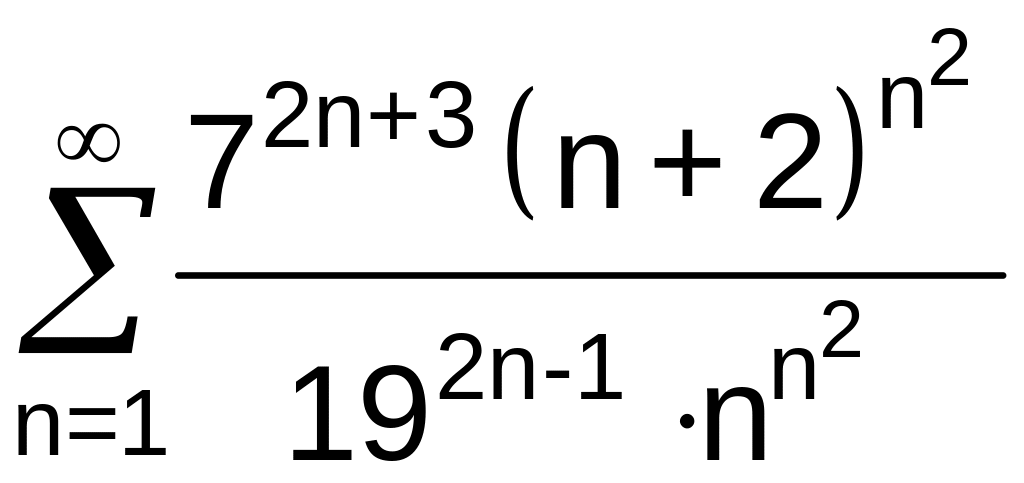
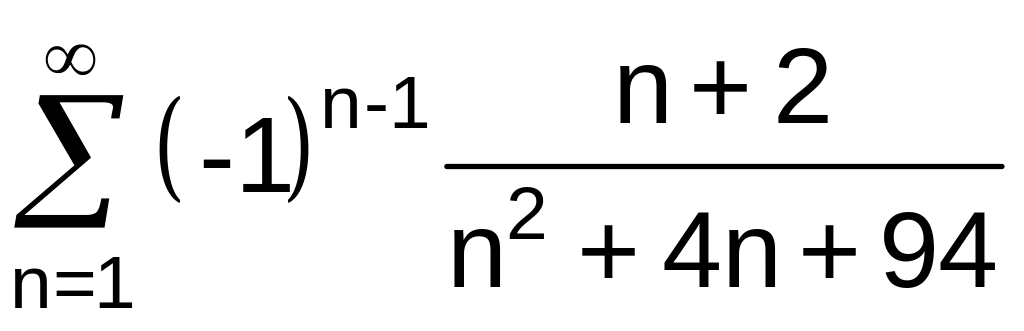 .
.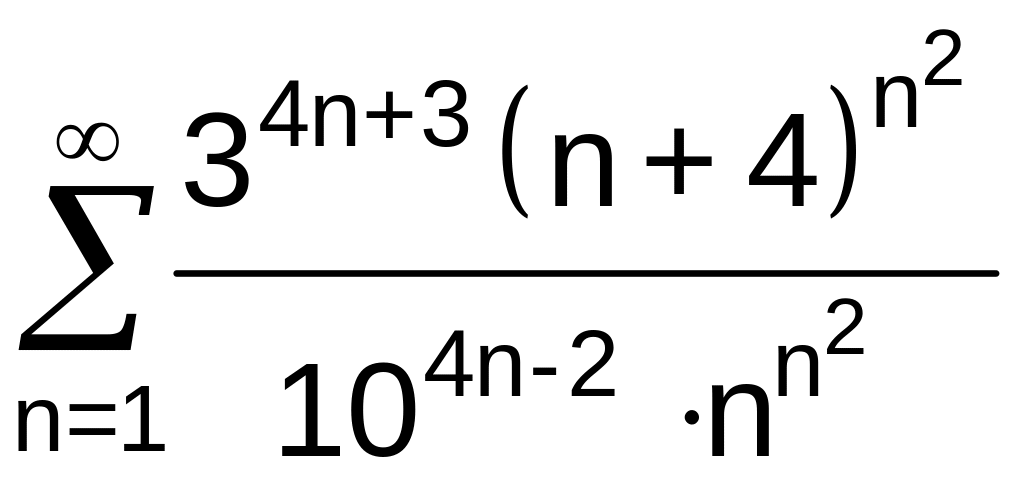
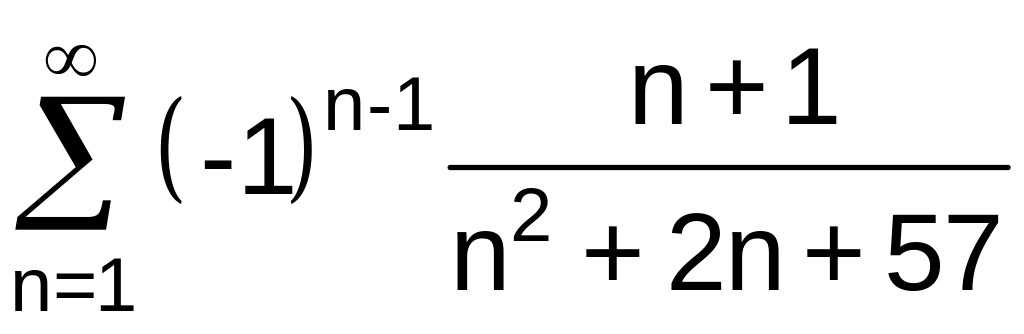 .
.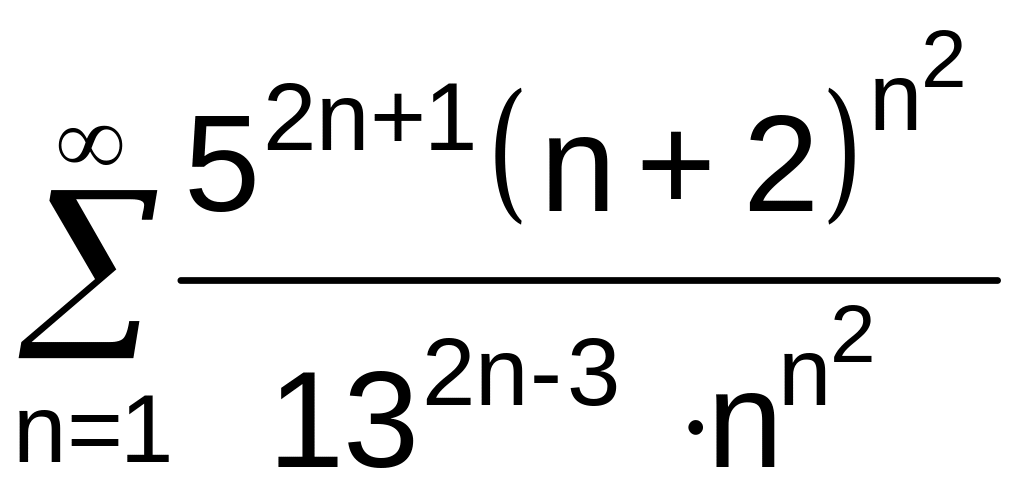
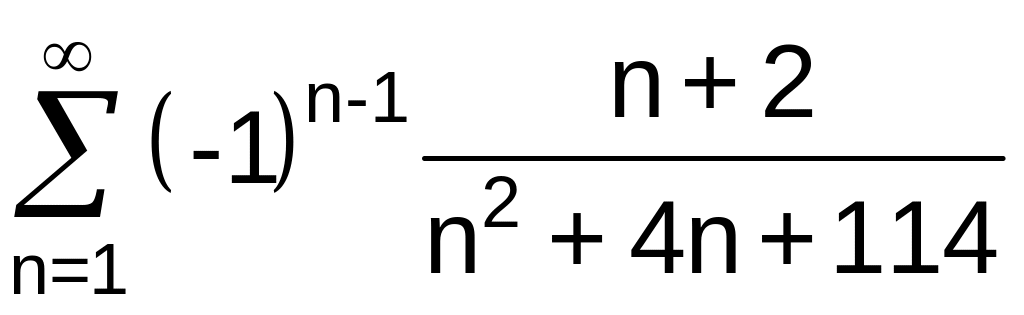 .
.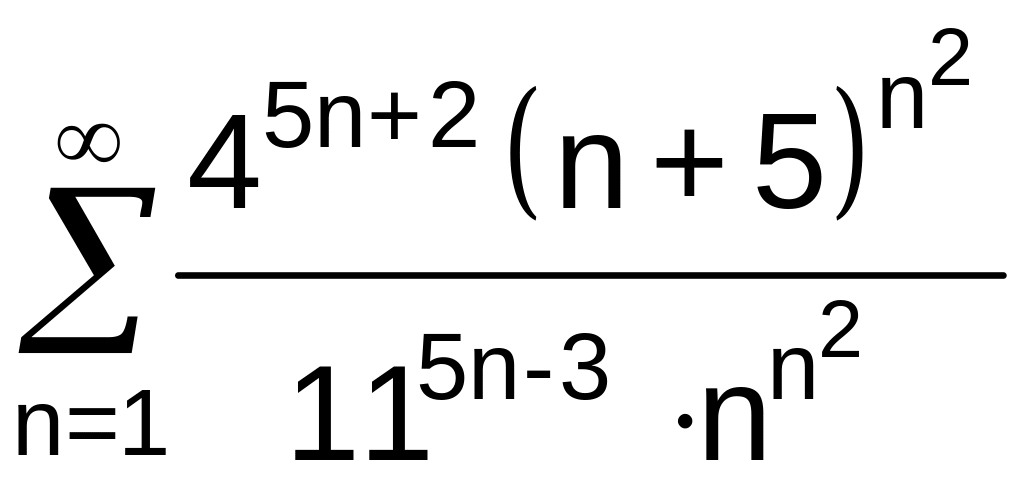
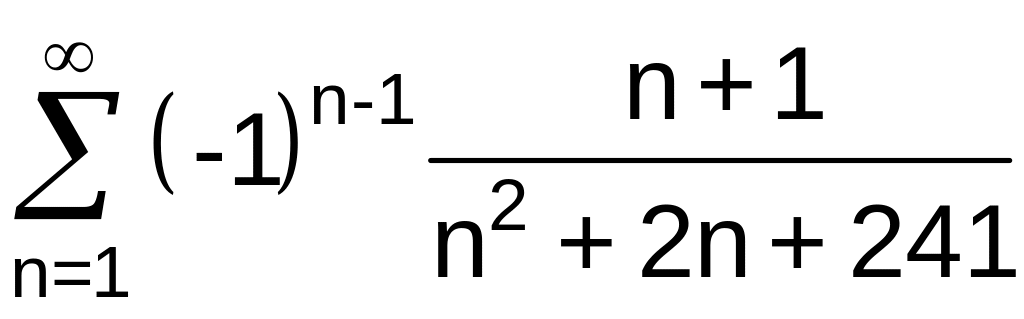 .
.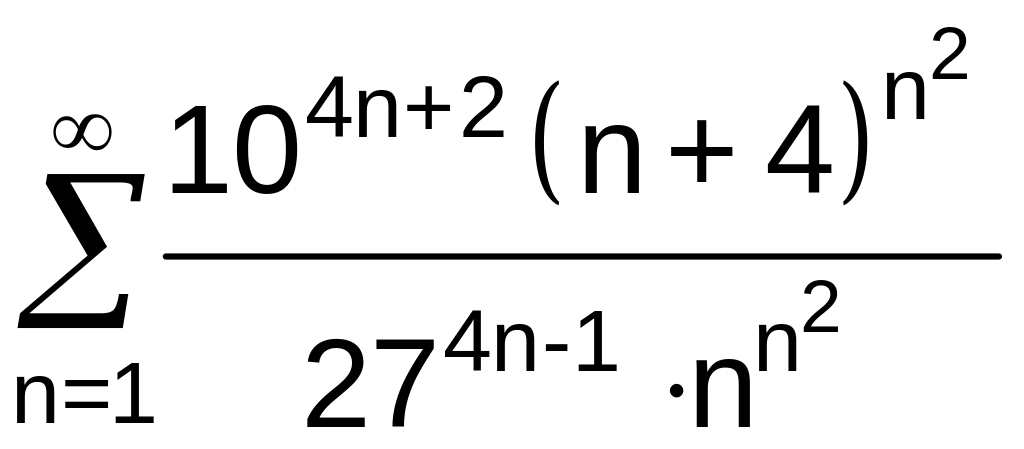
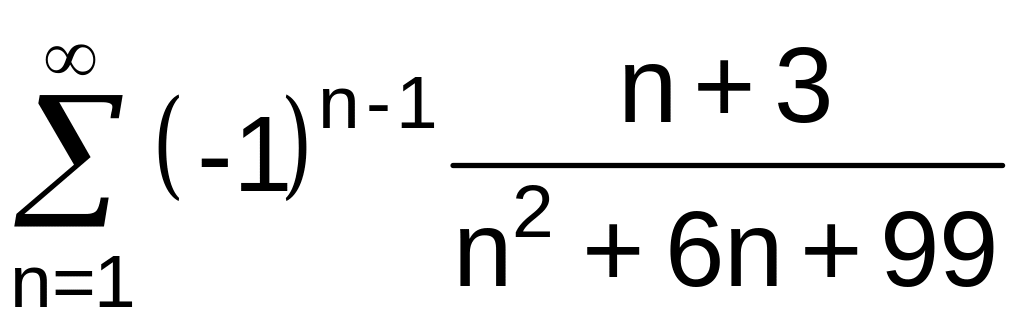 .
.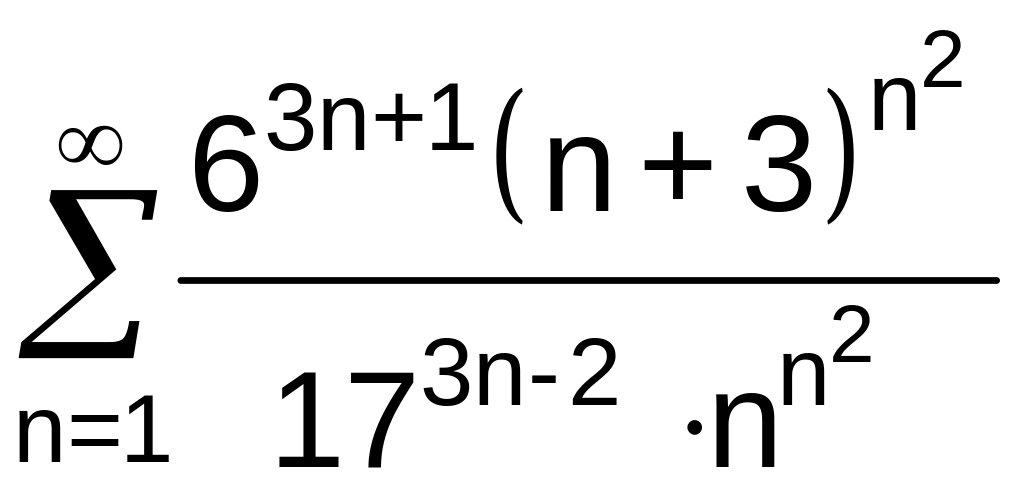
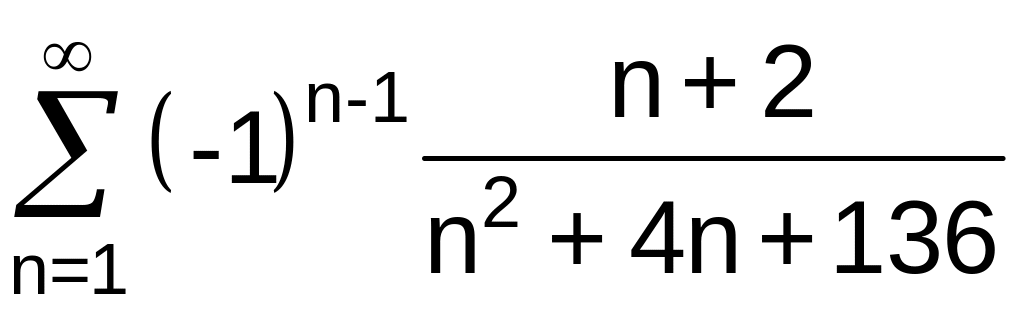 .
.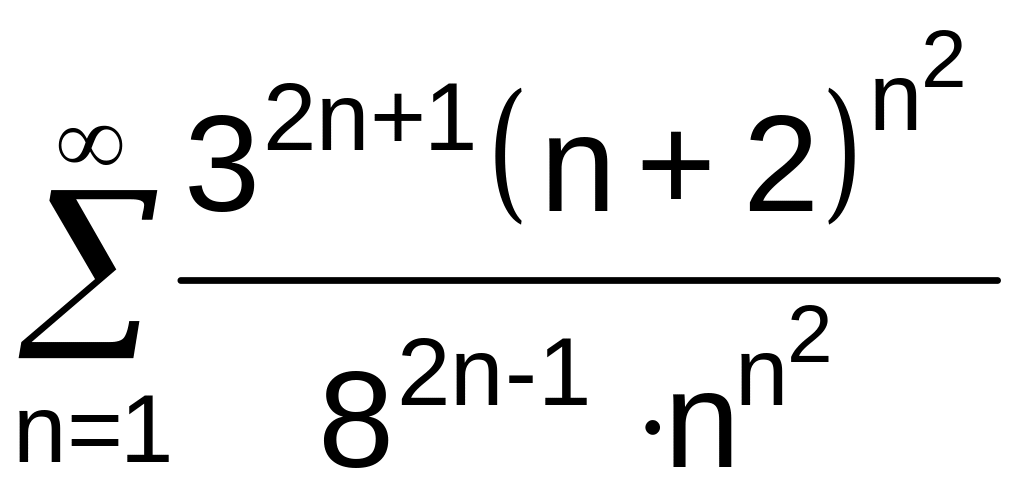
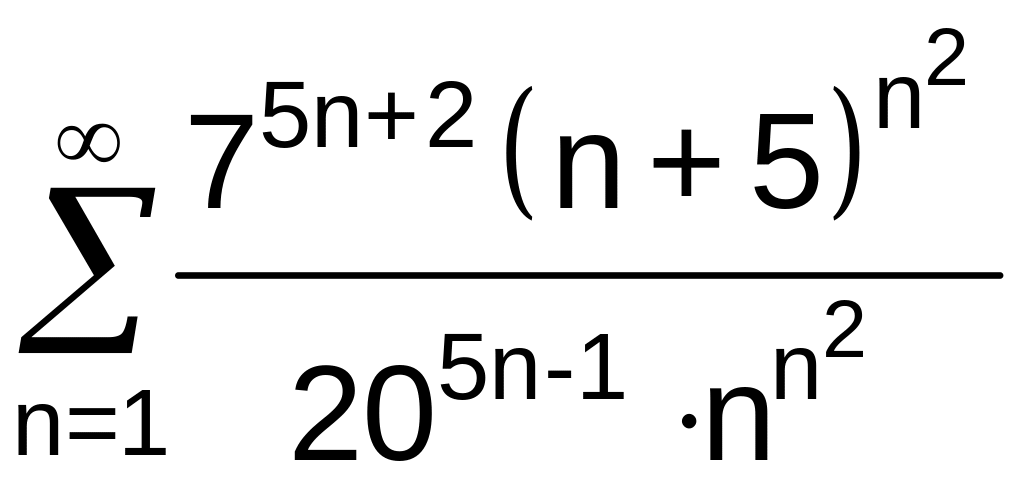
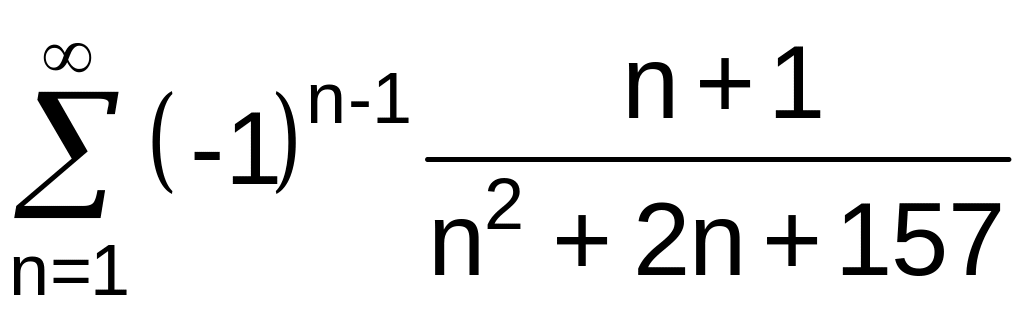 .
.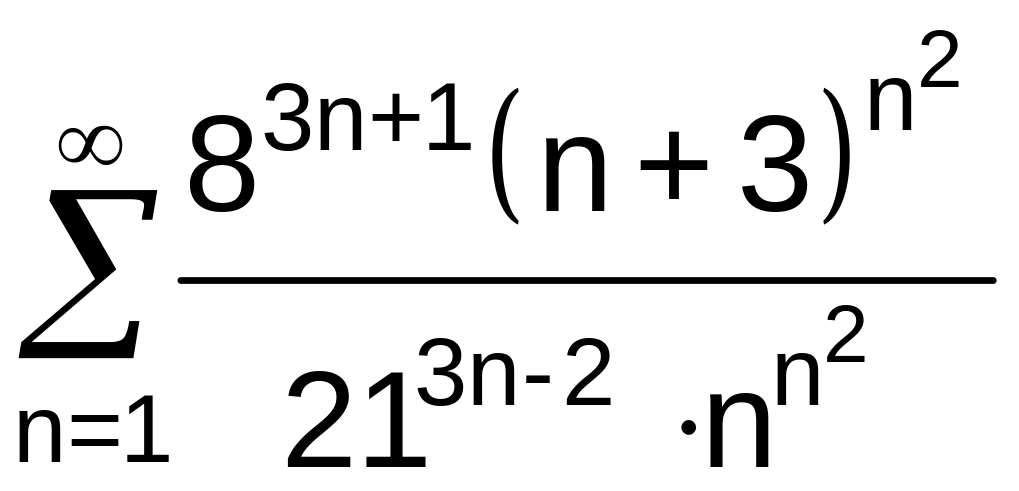
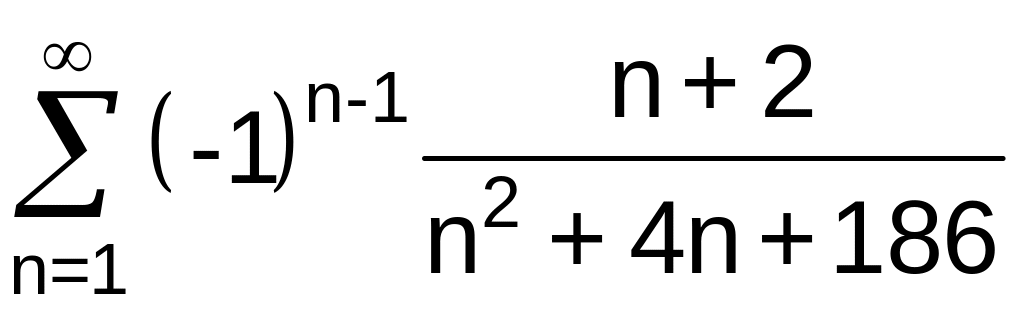 .
.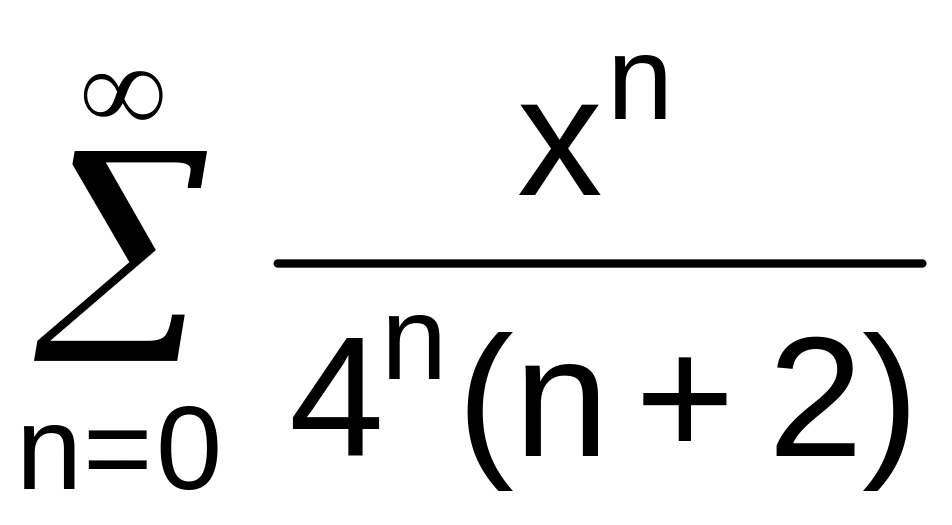 .
.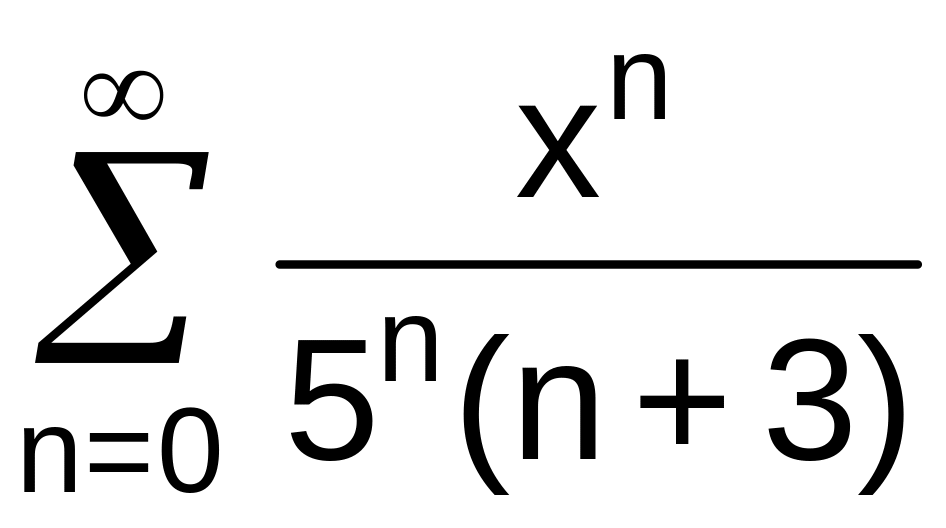 .
.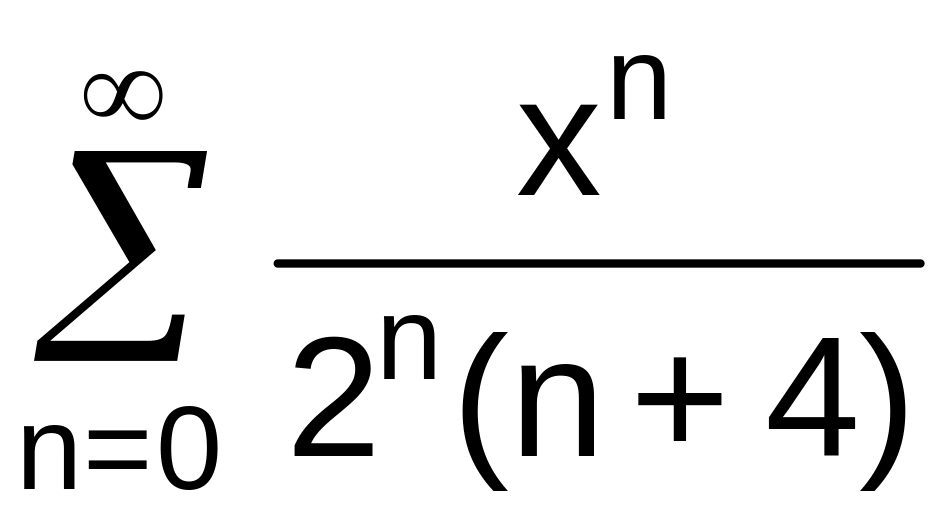 .
.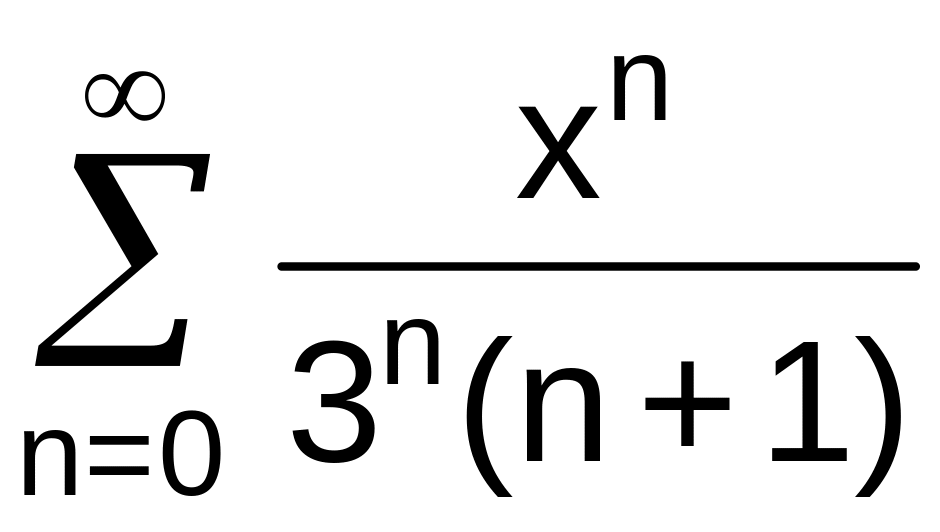 .
.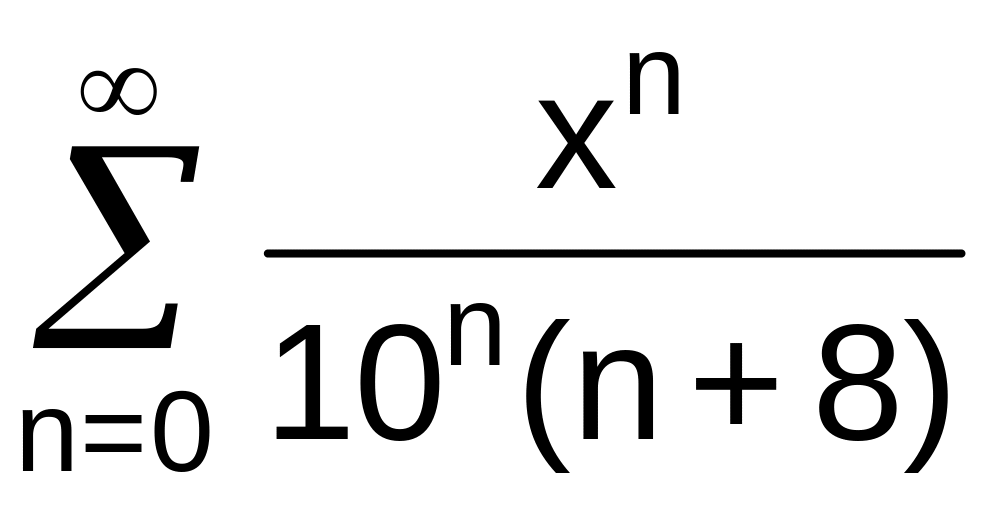 .
.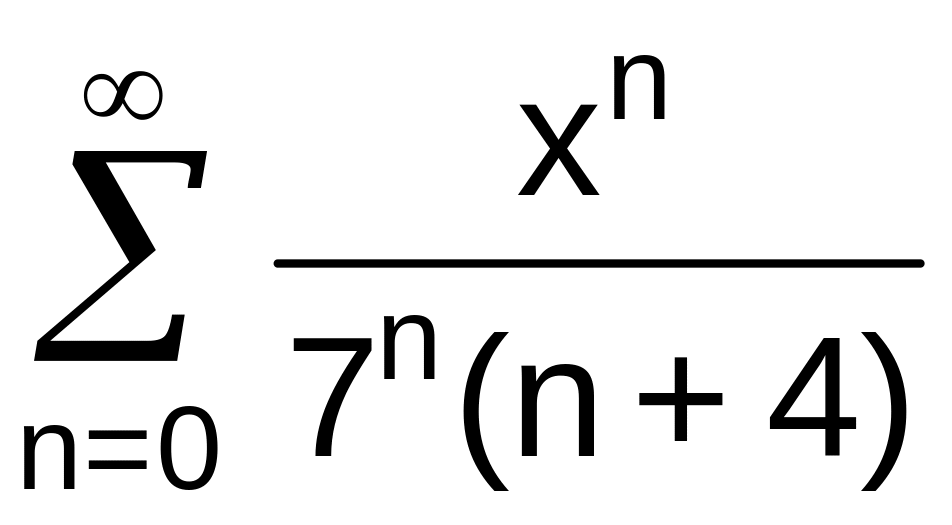 .
.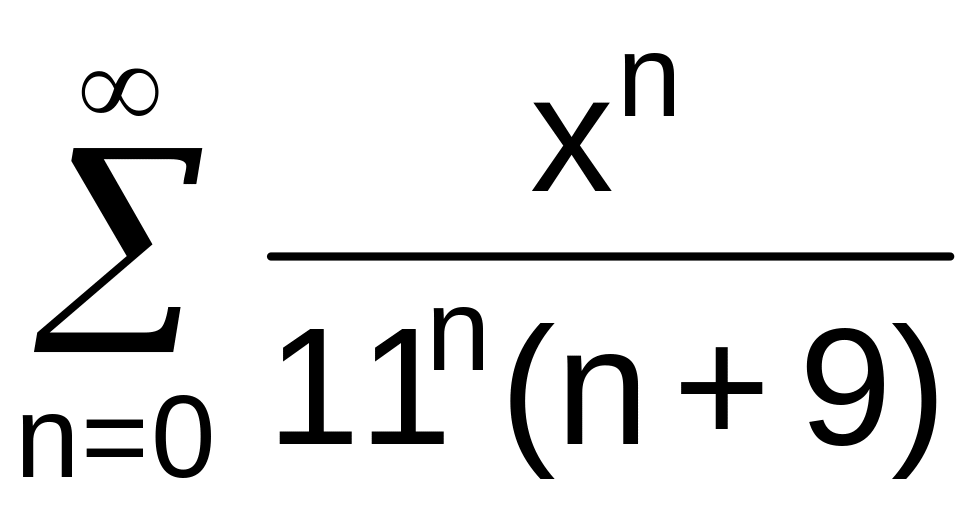 .
.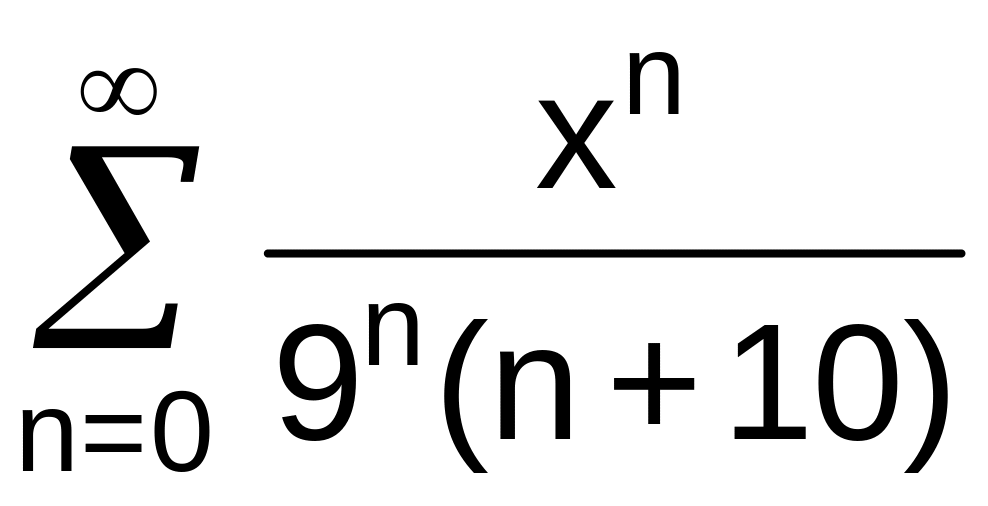 .
.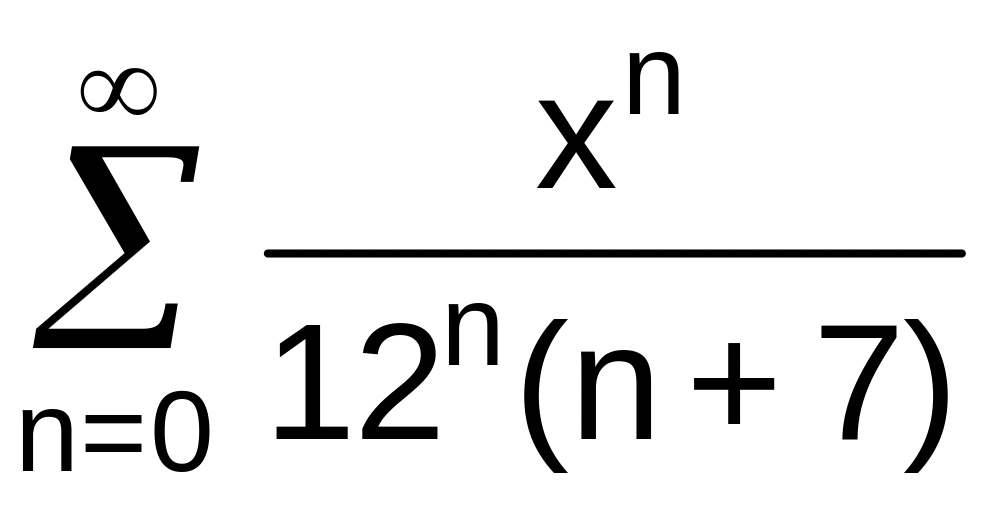 .
.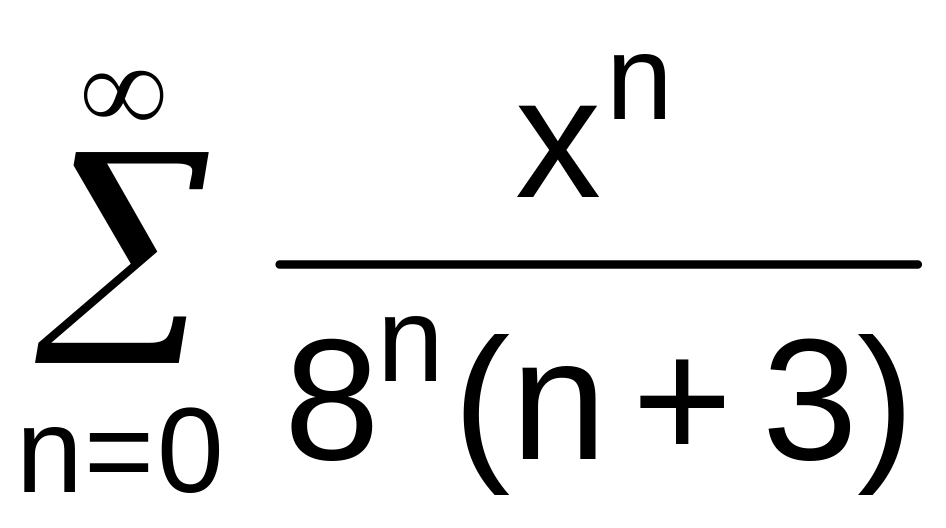 .
.